ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

ФИЛИАЛ В Г. УФЕ

РЕГИОНАЛЬНАЯ КАФЕДРА «МАТЕМАТИКА И ИНФОРМАТИКА»

ЛАБОРАТОРНАЯ РАБОТА № 2

ТЕМА: Моделирования и решения специальных задач линейного программирования.

Вариант 2

                                                  Выполнил: студентка Слабожанина Л. В.

                                                                      3 курса (дневная) 1 поток

                                                                      по специальности Финансы и кредит

                                                                      группы ФК-1-4,

                                                                      № зачетной книжки 06ффд40482

                                                  Проверил: Профессор Горбатков С.А.

Уфа-2007 г.

Транспортная задача

Задача 2.2. Компания, занимающаяся ремонтом автомобильных дорог, в следующем месяце будет проводить ремонтных работы на пяти участках автодорог. Песок на участки ремонтных работ может доставляться из трех карьеров, месячные объемы предложений по карьерам известны. Из планов производства ремонтных работ известны месячные объемы потребностей по участкам работ. Имеются экономические оценки транспортных затрат (в у.е.) на перевозку 1 тонны песку с карьеров на ремонтные участки.

Числовые данные для решения содержатся ниже в матрице планирования (повариантно).

Требуется:

1.  Предложить план перевозок песка на участки ремонта автодорог,  который обеспечивает минимальные совокупные транс­портные издержки.

2. Определить, что произойдет с оптимальным планом, если изменятся условия перевозок: а) появится запрет на перевозки от первого карьера до второго участка работ; б) по этой коммуника­ции будет ограничен объем перевозок 3 тоннами.

Участок работ Карьер	B1	B2	B3	B4	B5	Предложение
A1	3	3	5	3	1	500
A2	4	3	2	4	5	300
A3	3	7	5	4	1	100
Потребности	150	350	200	100	100

Таб. 1 Матрица планирования

Экономико-математическая модель задачи:

1. х_ij – объем песка i-го карьера к j-му участку работ.

С_ij  - цена 1 т. От i-го карьера к j-му участку работ.

M_i – мощность поставки предлагаемого i – го карьера.

М₁=500

М₂=300

М₃=100

N_j – потребность j –го участка работ ограничения 150, 350, 200, 100, 100.

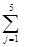х_ij=M_i         i=  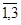(500, 300, 100)

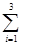x_ij=N_j          j= 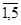(150, 350, 200, 100, 100)

X_ij=>0

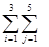F(x)=c_ij  x_ij  →  min

2.а. $C$3=0

2.б. $C$3<=3

Решение:

1.                Создание матрицы перевозок.

Для этого необходимо выполнить резервирование изменяемых ячеек, поэтому блок ячеек B3:E6 вводятся «1» - так резервирование место, где после решения задачи будет находиться распределение поставок, обеспечивающее минимальные затраты на перевозку груза.

2.                Ввод исходных данных.

Ввод мощности трех поставщиков. (А10:А12), потребности участка в песке (B9:F9), а также транспортные затраты (в у.е) на перевозку 1 тонны песку с карьеров на ремонтные участки (В9:F12).

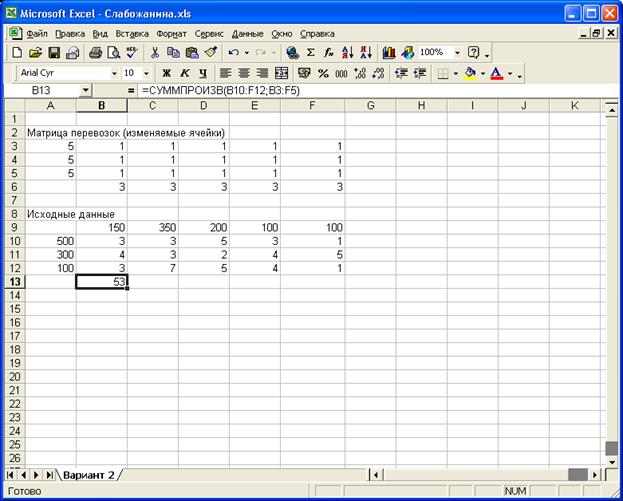
Рис. 1 ввода условий задачи.

3. Ввод граничных условий

Вводим условия реализации мощностей поставщиков:

А3=СУММ(B3:F3)

А4=СУММ(B4:F4)

А5 =СУММ(B5:F5)

Вводим условия удовлетворения запроса потребителей:

В6 =СУММ(B3:B5)

C6 =СУММ(C3:C5)

D6 =СУММ(D3:D5)

E6 =СУММ(E3:E5)

F6 =СУММ(F3:F5)

4. Целевой функции.

Целевая функции представляет собой произведение затрат на доставку песка (расположенных в блоке ячеек В10+F12) и объем песка для каждого потребителя (содержимое ячеек В3+F5).

B13 =СУММПРОИЗВ(B10:F12;B3:F5)

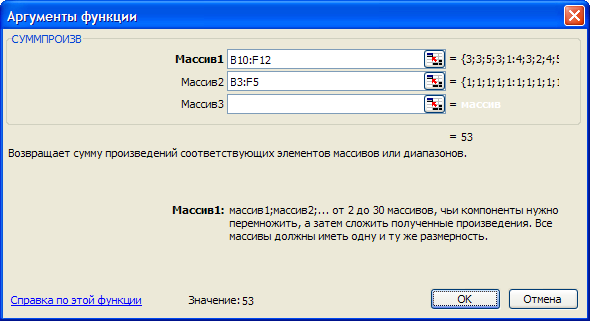
Рис. 2 Ввод целевой функций.

4.1. Ввод зависимостей из математической модели.

·                    Выберем Сервис → Поиск решения;

·                    Установим  целевую (ячейку) адрес $B$13 (тем самым мы резервируем ячейку, куда после решения задачи помещается значение целевой функций)

·                    Установить направление изменения целевой функции, равной Минимальному значению;

·                    Введем адреса изменяемых ячеек $B$3:$F$5

5.1. Ввод ограничений задачи

В матрицу перевозок, содержащую исходные данные по задаче, необходимо ввести условие реализации мощностей всех поставщиков .

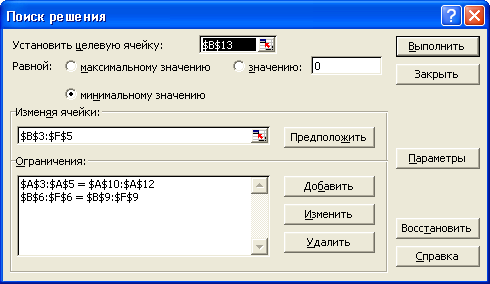
Рис. 3 Ввод зависимостей из математической модели.

6.1. Ввод параметров.

С помощью окна Параметры можно вводить условия для решения оптимизационных задач.

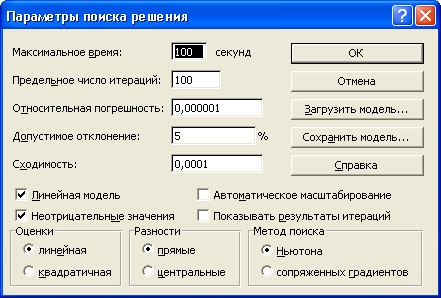
Рис.4 Ввод параметров.

7.1. Решения

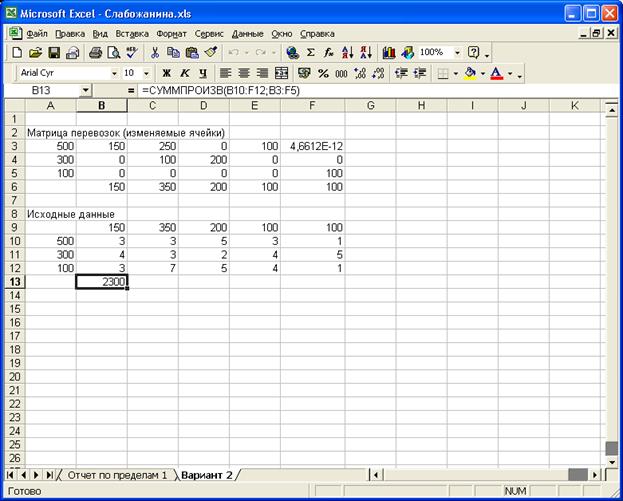
рис.5 Решение задачи

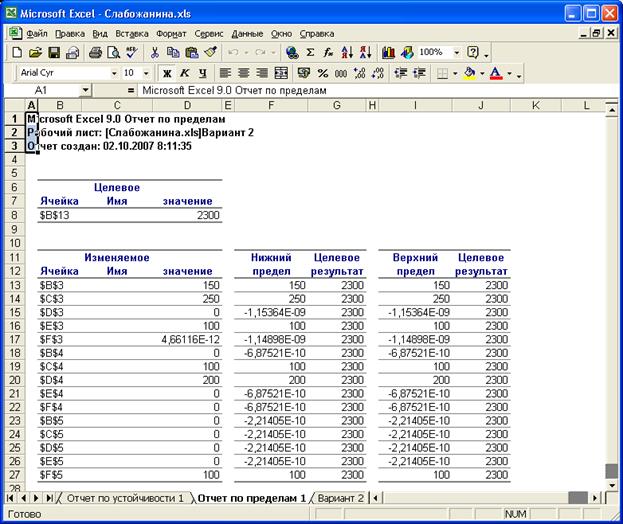
рис. 6 Отчет по пределам.

рис. 7 Отчет по устойчивости.

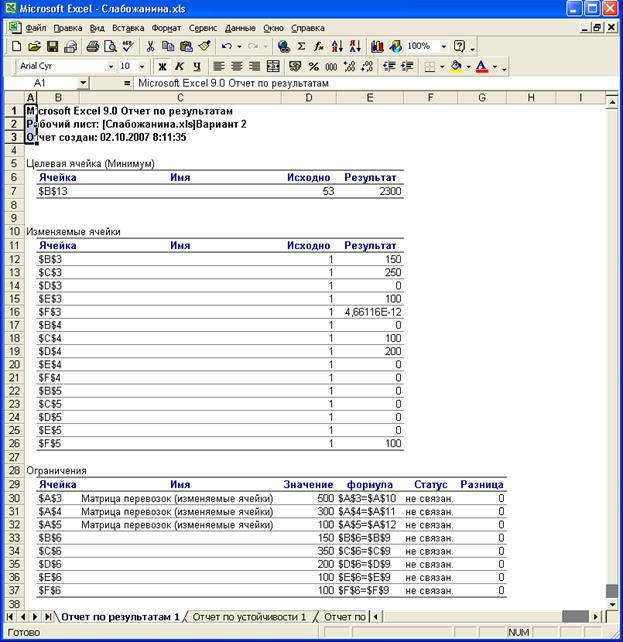
рис. 8 Отчет по результатам.

Предложение:

Полученное решение означает, что минимум затрат на доставку песка, равна 2300 условных единиц, будет обеспечен при следующем плане поставок:

·                   От первого поставщика первому потребителю в объеме 150 т., второму в объеме 250, четвертому в объеме 500 т., пятому в объеме 2 т.

·                   От второго поставщика второму потребителю в объеме 100 т., третьему в объеме 200 т.

·                   От третьего поставщика пятому потребителю в объеме 100 т.

При данной схеме поставок мощности всех поставщиков будут реализованы и спросы всех потребителей будут удовлетворены.

4.2.а Ввод зависимостей из математической модели.

·                    Выберем Сервис → Поиск решения;

·                    Установим  целевую (ячейку) адрес $B$13 (тем самым мы резервируем ячейку, куда после решения задачи помещается значение целевой функций)

·                    Установить направление изменения целевой функции, равной Минимальному значению;

·                    Введем адреса изменяемых ячеек $B$3:$F$5

5.2.а Ввод ограничений задачи

В матрицу перевозок, содержащую исходные данные по задаче, необходимо ввести условие реализации мощностей всех поставщиков

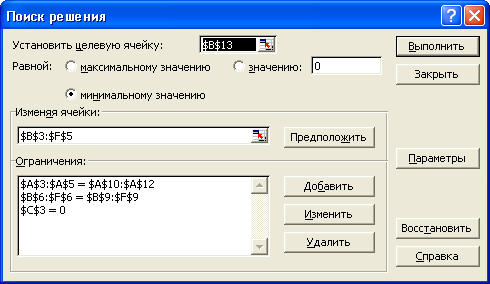
Рис. 9 Ввод зависимостей из математической модели.

6.2.a. Ввод параметров.

С помощью окна Параметры можно вводить условия для решения оптимизационных задач.

Рис.10 Ввод параметров.

7.1. Решения

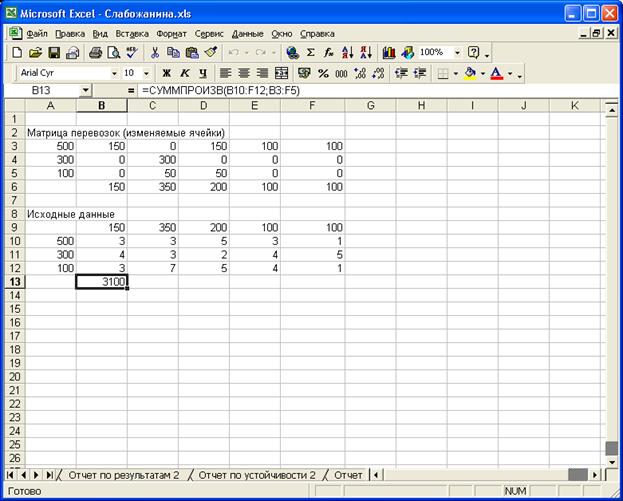
рис. 11 Решение задачи.

Рис. 12 Отчет по пределам

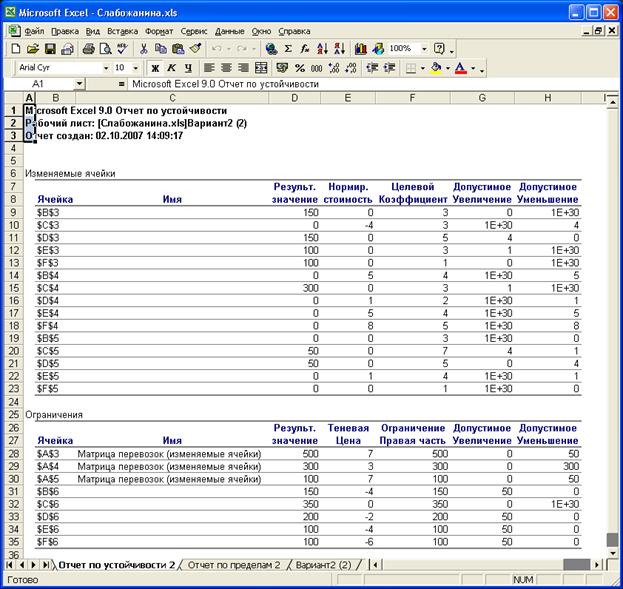
рис. 13 Отчет по устойчивости

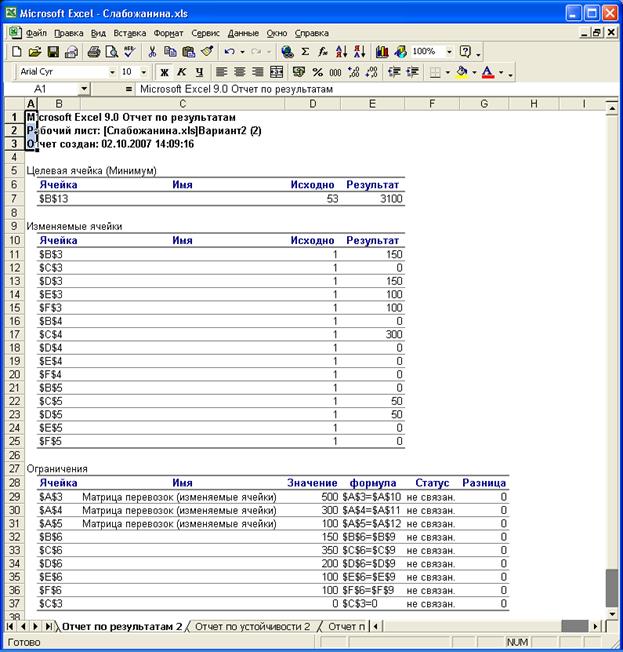
рис. 14 Отчет по результатам

Предложение:

При появления запрета на перевозки от первого карьера до второго участка работ, минимум затрат на доставку песка, составляет 3100 условных единиц, будет обеспечен при следующем плане поставок:

·                   От первого поставщика первому потребителю в объеме 150 т., третьему в объеме 150, четвертому в объеме 100 т., пятому в объеме 100 т.

·                   От второго поставщика второму потребителю в объеме 300 т.

·                   От третьего поставщика второму потребителю в объеме 50 т., третьему 50 т.

4.2.б Ввод зависимостей из математической модели.

·                    Выберем Сервис → Поиск решения;

·                    Установим  целевую (ячейку) адрес $B$13 (тем самым мы резервируем ячейку, куда после решения задачи помещается значение целевой функций)

·                    Установить направление изменения целевой функции, равной Минимальному значению;

·                    Введем адреса изменяемых ячеек $B$3:$F$5

5.2.а Ввод ограничений задачи

В матрицу перевозок, содержащую исходные данные по задаче, необходимо ввести условие реализации мощностей всех поставщиков

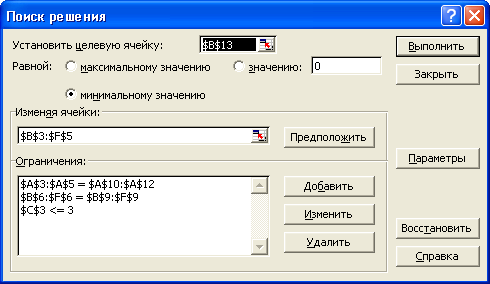
Рис. 15 Ввод зависимостей из математической модели.

6.2.б. Ввод параметров.

С помощью окна Параметры можно вводить условия для решения оптимизационных задач.

Рис.16 Ввод параметров.

7.1. Решения

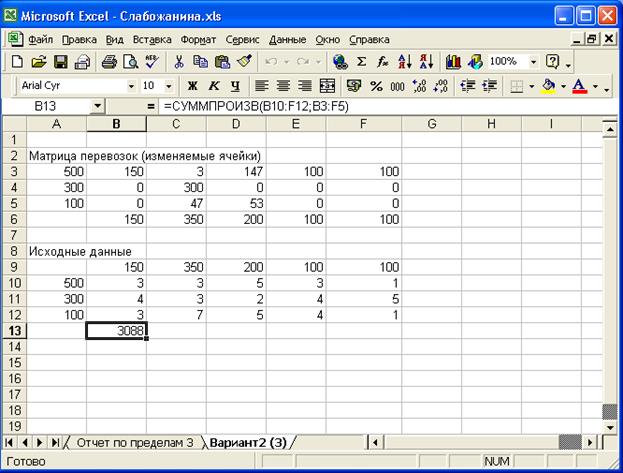
Рис. 17 Решение задачи.

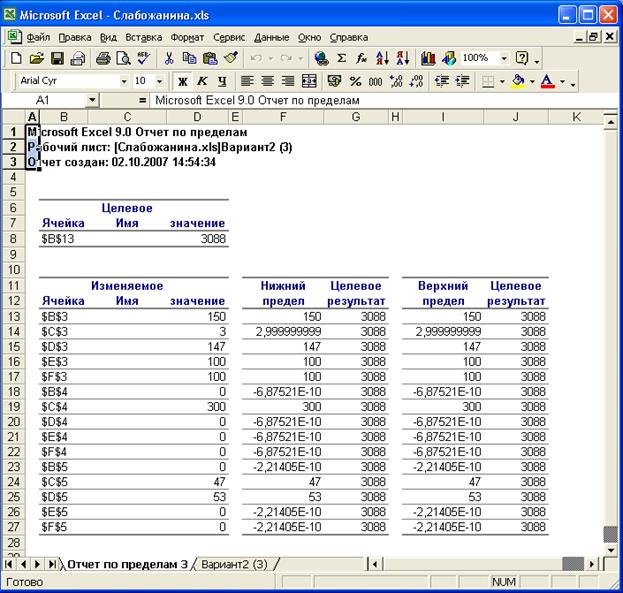
Рис. 18 Отчет по пределам.

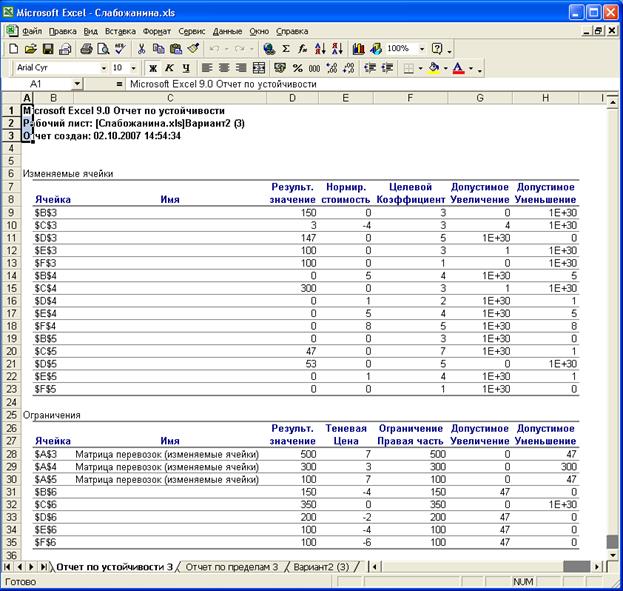
Рис. 19 Отчет по устойчивости.

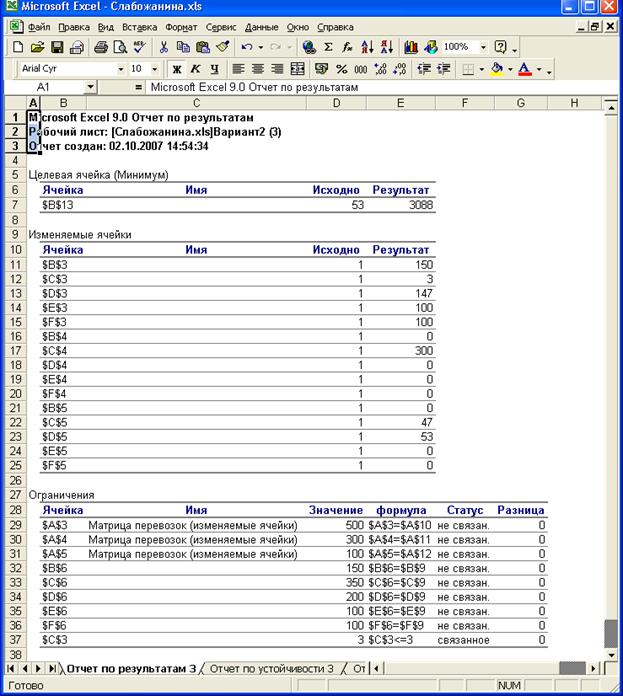
Рис. 20 Отчет по результатам.

Предложение:

При появления ограничение на перевозки (объем 3 тонна) от первого карьера до второго участка работ, минимум затрат на доставку песка, составляет 3088 условных единиц, будет обеспечен при следующем плане поставок:

·                   От первого поставщика первому потребителю в объеме 150 т., второму в объеме 3т., третьему в объеме 147 т., четвертому в объеме 100 т., пятому в объеме 100 т.

·                   От второго поставщика второму потребителю в объеме 300 т.

·                   От третьего поставщика второму потребителю в объеме 47 т., третьему 53 т.