ВСЕРОССИЙСКИЙ
ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА СТАТИСТИКИ
О Т Ч Е Т
о результатах выполнения
компьютерной лабораторной работы №1
«Автоматизированный априорный
анализ статистической совокупности
в среде MS Excel»
Вариант №
Постановка задачи
При проведении статистического
наблюдения за деятельностью предприятий корпорации получены выборочные данные
по 32-м предприятиям, выпускающим однородную продукцию (выборка 10%-ная, механическая), о
среднегодовой стоимости основных производственных фондов и о выпуске продукции за год.
В проводимом статистическом
исследовании обследованные предприятия выступают как единицы выборочной
совокупности, а показатели Среднегодовая
стоимость основных производственных фондов и Выпуск продукции – как изучаемые признаки единиц.
Для проведения
автоматизированного статистического анализа совокупности выборочные данные
представлены в формате электронных таблиц процессора Excel в диапазоне ячеек
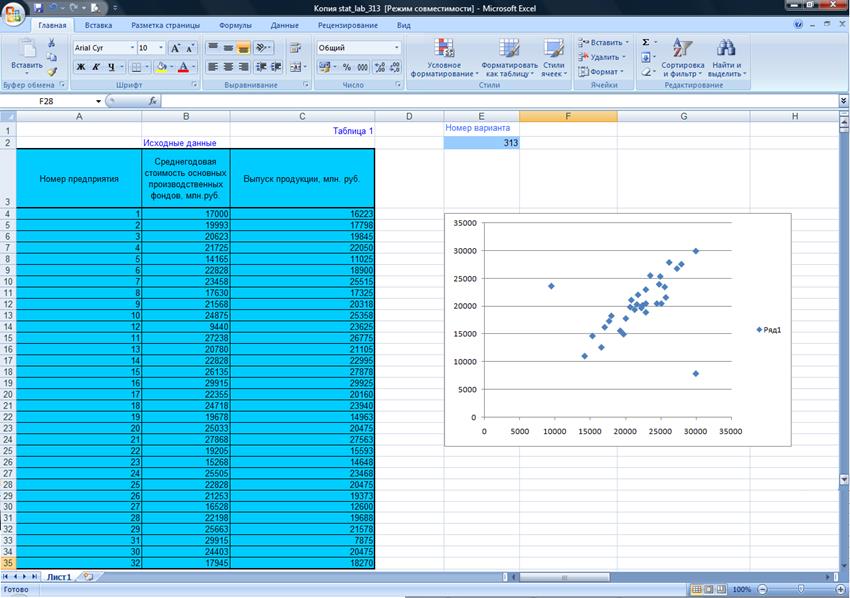
B4:C35. Для демонстрационного примера (ДП) выборочные данные приведены в табл.
1-ДП.
Таблица 1-ДП
Исходные данные
|
Номер предприятия
|
Среднегодовая стоимость основных
производственных фондов, млн.руб.
|
Выпуск продукции, млн. руб.
|
|
1
|
17000
|
16223
|
|
2
|
19993
|
17798
|
|
3
|
20623
|
19845
|
|
4
|
21725
|
22050
|
|
5
|
14165
|
11025
|
|
6
|
22828
|
18900
|
|
7
|
23458
|
25515
|
|
8
|
17630
|
17325
|
|
9
|
21568
|
20318
|
|
10
|
24875
|
25358
|
|
11
|
27238
|
26775
|
|
13
|
20780
|
21105
|
|
14
|
22828
|
22995
|
|
15
|
26135
|
27878
|
|
16
|
29915
|
29925
|
|
17
|
22355
|
20160
|
|
18
|
24718
|
23940
|
|
19
|
19678
|
14963
|
|
20
|
25033
|
20475
|
|
21
|
27868
|
27563
|
|
22
|
19205
|
15593
|
|
23
|
15268
|
14648
|
|
24
|
25505
|
23468
|
|
25
|
22828
|
20475
|
|
26
|
21253
|
19373
|
|
27
|
16528
|
12600
|
|
28
|
22198
|
19688
|
|
29
|
25663
|
21578
|
|
30
|
24403
|
20475
|
|
32
|
17945
|
18270
|
В процессе исследования
совокупности необходимо решить ряд статистических задач для выборочной
и генеральной совокупностей.
Статистический анализ выборочной
совокупности
1. Выявить
наличие среди исходных данных резко выделяющихся значений признаков («выбросов»
данных) с целью исключения из выборки аномальных единиц наблюдения.
2. Рассчитать
обобщающие статистические показатели совокупности по изучаемым признакам:
среднюю арифметическую (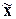 ), моду (Мо),
медиану (Ме), размах вариации (R), дисперсию(
), моду (Мо),
медиану (Ме), размах вариации (R), дисперсию(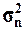 ), средние отклонения – линейное (
), средние отклонения – линейное (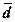 ) и квадратическое (σn),
коэффициент вариации (Vσ),
структурный коэффициент асимметрии
К.Пирсона (Asп).
) и квадратическое (σn),
коэффициент вариации (Vσ),
структурный коэффициент асимметрии
К.Пирсона (Asп).
3.
На основе рассчитанных показателей в
предположении, что распределения единиц по обоим признакам близки к
нормальному, оценить:
а) степень
колеблемости значений признаков в совокупности;
б) степень
однородности совокупности по изучаемым
признакам;
в)
устойчивость индивидуальных значений признаков;
г) количество попаданий
индивидуальных значений признаков в диапазоны (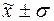 ), (
), (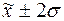 ), (
), (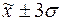 ).
).
4.
Дать сравнительную характеристику распределений
единиц совокупности по двум изучаемым признакам на основе анализа:
а) вариации
признаков;
б)
количественной однородности единиц;
в) надежности
(типичности) средних значений признаков;
г) симметричности распределений в
центральной части ряда.
5. Построить
интервальный вариационный ряд и гистограмму распределения единиц совокупности
по признаку Среднегодовая стоимость
основных производственных фондов и установить характер (тип) этого
распределения. Рассчитать моду Мо
полученного интервального ряда и сравнить ее с показателем Мо несгруппированного ряда данных.
Статистический
анализ генеральной совокупности
1.
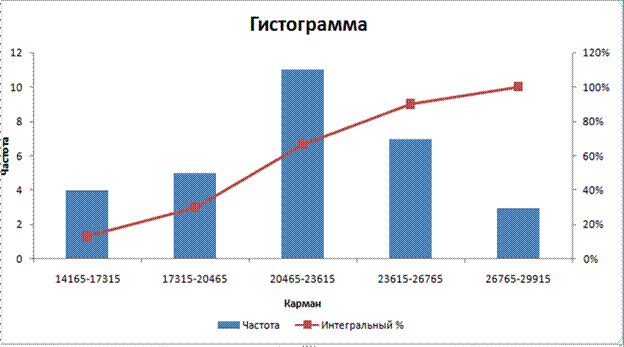
Рассчитать генеральную дисперсию 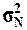 , генеральное
среднее квадратическое отклонение
, генеральное
среднее квадратическое отклонение 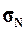 и
ожидаемый размах вариации признаков RN. Сопоставить значения этих
показателей для генеральной и выборочной дисперсий.
и
ожидаемый размах вариации признаков RN. Сопоставить значения этих
показателей для генеральной и выборочной дисперсий.
2.
Для изучаемых признаков рассчитать:
а) среднюю ошибку выборки;
б)
предельные ошибки выборки для уровней надежности P=0,683, P=0,954, P=0,997 и
границы, в которых будут находиться средние значения признака генеральной
совокупности при заданных уровнях надежности.
3.
Рассчитать коэффициенты асимметрии As и эксцесса Ek. На основе полученных оценок
сделать вывод о степени близости распределения единиц генеральной
совокупности к нормальному распределению.
Результативные таблицы
В процессе исследования совокупности необходимо решить ряд
статистических задач для выборочной и
генеральной совокупностей.
Статистичемкий анализ
генеральной совокупности
|
|
|
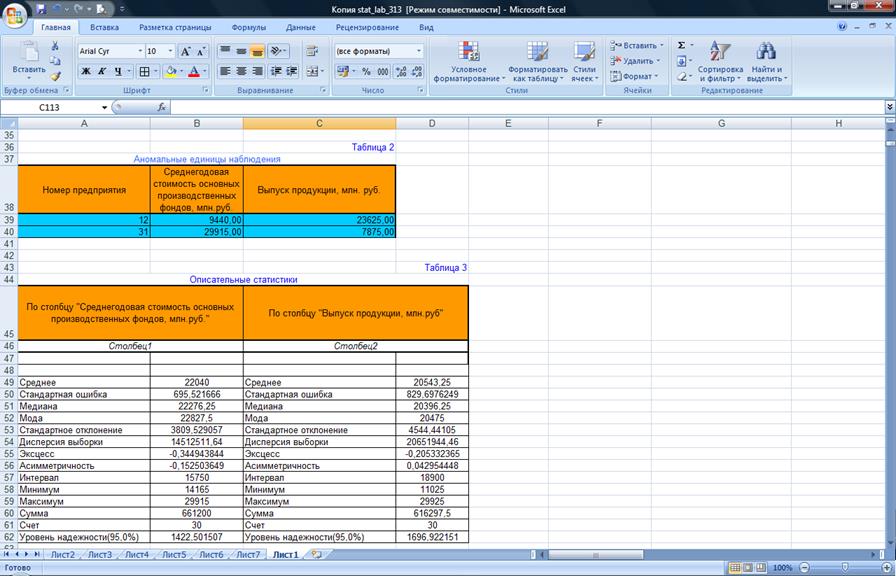
Таблица 2
|
|
Аномальные единицы наблюдения
|
|
Номер
предприятия
|
Среднегодовая
стоимость основных производственных фондов, млн.руб.
|
Выпуск
продукции, млн. руб.
|
|
12
|
9440,00
|
23625,00
|
|
31
|
29915,00
|
7875,00
|
Приведенные в
табл.2 аномальные единицы наблюдения удалены из изучаемой совокупности с целью
повышения степени ее однородности и статистической точности оценок расчетных
показателей. Аномальные единицы наблюдения подлежат индивидуальному анализу с
точки зрения «законности» причинах появления в совокупности.
Приведенные в таблице аномальные единицы наблюдения удалены
из изучаемой совокупности. Корреляционное поле имеет вид:
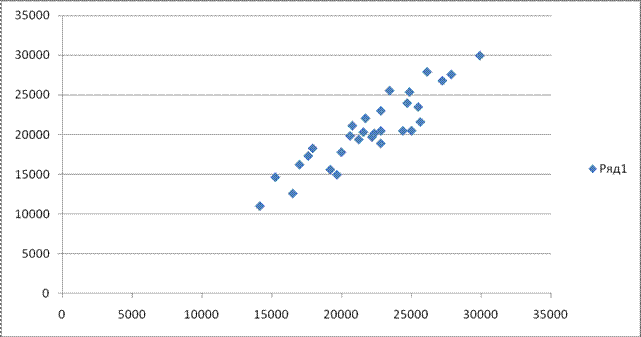
2. Выборочные
показатели в результате расчетов представлены в 2-х таблицах – Таблица 3 и
Таблица 5
|
|
|
Таблица 3
|
|
Описательные
статистики
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов, млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Столбец1
|
Столбец2
|
|
|
|
|
|
|
|
|
|
|
|
Среднее
|
22040
|
Среднее
|
20543,25
|
|
Стандартная
ошибка
|
695,521666
|
Стандартная
ошибка
|
829,6976249
|
|
Медиана
|
22276,25
|
Медиана
|
20396,25
|
|
Мода
|
22827,5
|
Мода
|
20475
|
|
Стандартное
отклонение
|
3809,529057
|
Стандартное
отклонение
|
4544,44105
|
|
Дисперсия
выборки
|
14512511,64
|
Дисперсия
выборки
|
20651944,46
|
|
Эксцесс
|
-0,344943844
|
Эксцесс
|
-0,205332365
|
|
Асимметричность
|
-0,152503649
|
Асимметричность
|
0,042954448
|
|
Интервал
|
15750
|
Интервал
|
18900
|
|
Минимум
|
14165
|
Минимум
|
11025
|
|
Максимум
|
29915
|
Максимум
|
29925
|
|
Сумма
|
661200
|
Сумма
|
616297,5
|
|
Счет
|
30
|
Счет
|
30
|
|
Уровень
надежности(95,0%)
|
1422,501507
|
Уровень
надежности(95,0%)
|
1696,922151
|
|
|
|
|
|
|
|
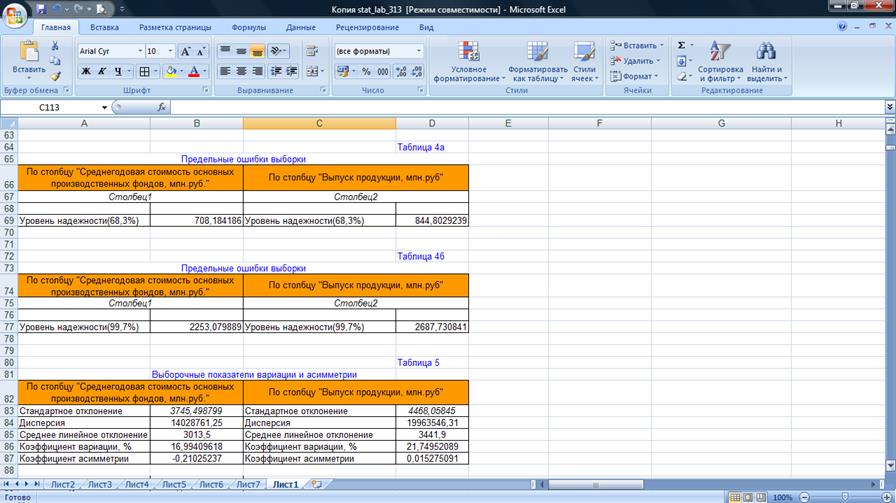
Таблица 4а
|
|
Предельные
ошибки выборки
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
|
Уровень
надежности(68,3%)
|
708,184186
|
Уровень
надежности(68,3%)
|
844,8029239
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4б
|
|
Предельные
ошибки выборки
|
|
По столбцу "Среднегодовая
стоимость основных производственных фондов, млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Столбец1
|
Столбец2
|
|
|
|
|
|
|
Уровень
надежности(99,7%)
|
2253,079889
|
Уровень
надежности(99,7%)
|
2687,730841
|
|
|
|
|
Таблица 5
|
|
Выборочные показатели вариации
и асимметрии
|
|
|
По столбцу "Среднегодовая
стоимость основных производственных фондов, млн.руб."
|
По столбцу "Выпуск продукции,
млн.руб"
|
|
Стандартное отклонение
|
3745,498799
|
Стандартное отклонение
|
4468,05845
|
|
Дисперсия
|
14028761,25
|
Дисперсия
|
19963546,31
|
|
Среднее линейное отклонение
|
3013,5
|
Среднее линейное отклонение
|
3441,9
|
|
Коэффициент вариации, %
|
16,99409618
|
Коэффициент вариации, %
|
21,74952089
|
|
Коэффициент асимметрии
|
-0,21025237
|
Коэффициент асимметрии
|
0,015275091
|
|
|
|
|
|
|
3. а) после
удаления аномальных значений коэффициент вариации Vσ:
1. признака «Среднегодовая стоимость основных
производственных фондов» составляет 16,9941%, исходя из оценочной шкалы
находится в диапазоне 0%<Vσ≤40%. – колеблемость
незначительная;
2. признака «Выпуск продукции» составляет 21,7495%, исходя их оценочной
шкалы находится в диапазоне 0%< Vσ≤40%. – колеблемость незначительная.
б) однородность совокупности для нормального и
близких к нормальному распределений устанавливается по условию: Vσ≤33%.
Коэффициент вариации Vσ признака «Среднегодовая
стоимость основных производственных фондов» составляет 16,9941%, что свидетельствует
об однородности изучаемой совокупности.
Коэффициент вариации Vσ признака «Выпуск продукции» составляет 21,7495%,
что свидетельствует об однородности изучаемой совокупности.
Чем однороднее изучаемая совокупность, тем надежнее полученная средняя.
в) Сопоставление средних отклонений –
квадратического σ и линейного 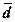 позволяет сделать вывод об устойчивости индивидуальных
значений признака, т.е. об отсутствии среди них «аномальных» вариантов
значений.
позволяет сделать вывод об устойчивости индивидуальных
значений признака, т.е. об отсутствии среди них «аномальных» вариантов
значений.
|
По столбцу «Среднегодовая стоимость
основных производственных фондов, млн. руб.»
|
По столбцу «Выпуск продукции, млн. руб.»
|
|
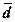 /σ /σ
0,80
|
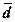 /σ /σ
0,77
|
Отношение показателей σ и 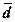 может служить
индикатором устойчивости данных:
может служить
индикатором устойчивости данных:
если 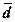 /σ < 0,8, то
можно сделать вывод об устойчивости индивидуальных значений признака, среди них
отсутствуют «аномальные» выбросы.
/σ < 0,8, то
можно сделать вывод об устойчивости индивидуальных значений признака, среди них
отсутствуют «аномальные» выбросы.
Так как это условие соблюдается, то можно сделать вывод об
устойчивости индивидуальных значений признака Среднегодовая стоимость основных производственных фондов и признака
Выпуск продукции, то есть среди них
отсутствуют «аномальные» варианты значений, значения признака устойчивы.
г)
|
Признаки
|
Количество значений признака Xi, находящихся в диапазоне
|
|
x- σn≤
Xi≤ x+ σn
|
x-2σn≤
Xi≤ x+2σn
|
x-3σn≤
Xi≤ x+3σn
|
|
1. Среднегодовая
стоимость основных производственных фондов
|
20
18295≤ Xi≤25785
|
28
14549≤ Xi≤29531
|
31
10804≤ Xi≤33276
|
|
2. Выпуск продукции
|
20
16075≤ Xi≤25011
|
29
11607≤ Xi≤29479
|
31
7139≤ Xi≤33947
|
По значениям показателей xi и σ можно
определить границы интервалов вариации признака, т.е. установить, какая доля
единиц совокупности попадает в тот или иной интервал отклонений значений
признака от xi.
В нормально распределенных и близких к ним рядах
вероятностные оценки границ интервалов таковы:
68,3% значений признака войдет в интервал 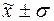 ;
;
95,4% значений признака попадет в интервал 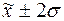 ;
;
99,7% значений признака появится в интервале 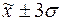 .
.
Следовательно,
Для признака
среднегодовая стоимость основных фондов:
68,3% значений признака
войдет в интервал от 18295 до 25785;
95,4% значений признака
попадет в интервал от 14549 до 29531;
99,7% значений признака
появится в интервале от 10804 до 33276.
Для признака выпуск
продукции:
68,3% значений признака
войдет в интервал от 16075 до 24289;
95,4% значений признака попадет в интервал от 11607
до 28034;
99,7% значений признака появится в интервале от 7139 до
31780.
Ожидаемые границы
вариации выборки для признака «Среднегодовая стоимость основных
производственных фондов» соответствует:
±σ с
вероятностью Р = 68,3%, т.е. ±3745;
±2σ с вероятностью Р = 95,4%, т.е. ±7491;
±3σ с вероятностью Р = 99,7%, т.е. ±11236.
Ожидаемые границы
вариации выборки для признака «Выпуск продукции» соответствует:
±σ с
вероятностью Р = 68,3%, т.е. ±4468;
±2σ с вероятностью Р = 95,4%, т.е. ±8396;
±3σ с вероятностью Р = 99,7%, т.е. ±13404.
Для обоих признаков рассчитанные значения процентное
соотношение рассеяния отличаются на незначительную величину от вероятных оценок
диапазонов рассеяния.
4. а) Так как,
значение показателя вариации Vσ = 16,9941% для признака «Среднегодовая
стоимость основных производственных фондов», а Vσ = 21,7495% для
признака «Выпуск продукции», то индивидуальные значения признака «Среднегодовая
стоимость основных производственных фондов», мало отличаются друг от
друга, единицы наблюдения количественно более однородны, чем для признака
«Выпуск продукции».
б) Так как
значение Vσ для обоих признаков невелико, т.е. Vσ≤33%, следовательно, средняя арифметическая величина
является надежной характеристикой данной совокупности.
в) По таблице 5 видно,
что Asп < 0 (Asп =
-0,2103) для признака «Среднегодовая стоимость основных производственных
фондов», и это означает, что асимметрия левосторонняя, для которой справедливо
равенство
xс
< Me
< Mo,
означающее, что в распределении чаще встречаются более низкие
значения признака, а для признака «Выпуск продукции» Asп
> 0, т.е.
Asп = 0,0153, и это значит, что асимметрия правосторонняя,
для которой справедливо неравенство x
> Me
>Mo,
означающее, что в распределении чаще встречаются более высокие значения
признака.
г) Для обеих
признаков |As| ≤
0,25 – асимметрия незначительная, значит основная масса единиц располагается в
центральной зоне ряда, но для признака «Выпуск продукции» форма кривой
значительнее ближе к распределению нормальной кривой.
5.
|
|
|
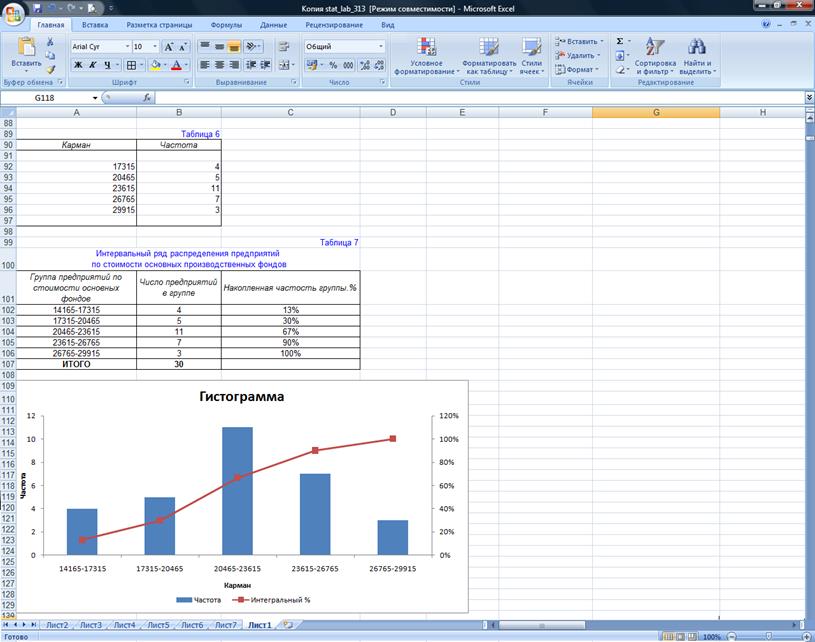
Таблица 7
|
|
Интервальный ряд распределения предприятий
по стоимости основных производственных
фондов
|
|
Группы
предприятий по стоимости основных фондов
|
Число
предприятий в группе
|
Накопленная
частость группы
|
|
14165-17315
|
4
|
13%
|
|
17315-20465
|
5
|
30%
|
|
20465-23615
|
11
|
67%
|
|
23615-26765
|
7
|
90%
|
|
26765-29915
|
3
|
100%
|
|
ИТОГО
|
30
|
|
Для полученного интервального ряда рассчитываем значение
моды Mo:
Mo =
XMo + IMo * (fMo - fMo ) / (( fMo – fMo-1)
+ (fMo
+ fMo+1))
=
=20465 + 3150 * (11 -5) / (11 – 5) + (11 – 7) = 22355 (млн.
руб.)
Расхождения между полученными значениями Мо и значениями
моды из таблицы 3, т.е. Мо = 22827,5 млн. руб. объясняется тем, что значение Мо
= 22355 млн. руб. получено по фактическим значениям, а для интервального ряда –
по центральным значениям.
Статистический анализ генеральной совокупности
1. Установим
степень расхождения между уn2 и yN2
по формуле:
Для признака «Среднегодовая стоимость основных
производственных фондов»
σ N2
/ σn2
= 14512511,64 / 14028761,25 = 1,03448
Для признака «Выпуск продукции»
σ N2 / σn2 = 20651944,46 / 19963546,31 = 1,03448
Степень расхождения: σ N2 / σn2 = n / n-1 = 30 / 29 = 1,034
Степень расхождения между уn2 и yN2 для обоих признаков отсутствует.
Рассчитываем прогнозные оценки размаха вариации RN и
сравниваем с Rn:
Для признака «Среднегодовая стоимость основных
производственных фондов»
RN = 6σ = 6 * 3 809,5 = 22857
Rn=
6σ = 6 * 3 745,5 = 22473
R = 22857
– 22473 = 384
Для признака «Выпуск продукции»
RN = 6σ = 6 * 4 544,4 = 27266,4
Rn = 6σ = 6 * 4 468,1 = 26806,6
R = 27266,4
– 26806,6 = 457,8
Прогнозные оценки размаха вариации для обоих признаков
практически отсутствуют.
2. а) Для
признака «Среднегодовая стоимость основных производственных фондов» - 695,5млн.
руб.
Для признака «Выпуск продукции» - 829,7 млн. руб.
б) Хср-∆Х
≤Хср≤Хср +∆Х
предельную ошибку выборки найдем по формуле
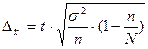
t – коэффициент
доверия,
|
Дове-рительная вероят-
ность Р
|
Коэффи-
циент
доверия t
|
Предельные ошибки выборки
|
Ожидаемые границы для средних
|
|
Для первого
признака
|
Для второго
признака
|
Для первого
признака
|
Для второго
признака
|
|
0,683
|
1
|
649
|
774
|
21 391
|
-
|
22 689
|
19 769
|
-
|
21 317
|
|
0,954
|
2
|
1 297
|
1 548
|
20 743
|
-
|
1 297
|
18 995
|
-
|
22 091
|
|
0,997
|
3
|
1 946
|
2 322
|
20 094
|
-
|
23 337
|
18 222
|
-
|
22 865
|
3. AsN = |0,2102| - указывает
на незначительную величину асимметрии, а
EkN = -0,345 указывает на умеренную величину эксцесса
соответственно, то есть основание полагать, что распределение единиц
генеральной совокупности по признаку «Среднегодовая стоимость основных
производственных фондов», будет близко к нормальному. Распределение единиц
генеральной совокупности по признаку «Выпуск продукции» AsN = 0,0152 и EkN = -0,205
указывает на незначительную величину асимметрии и эксцесса соответственно.
Вывод
1) После удаления аномальных значений коэффициент вариации Vσ признака
«Среднегодовая стоимость основных производственных фондов» составляет 17,0112%,
исходя из оценочной шкалы находится в диапазоне 0%< Vσ≤40%. – колеблемость
незначительная.
Однородность совокупности для нормального и близких к нормальному
распределений устанавливается по условию: Vσ≤33%.
Коэффициент вариации Vσ признака «Среднегодовая стоимость основных
производственных фондов» составляет 17,0112%, что свидетельствует об однородности
изучаемой совокупности.
Коэффициент вариации Vσ признака «Выпуск продукции» составляет 16,9941%,
что свидетельствует об однородности изучаемой совокупности.
Чем однороднее изучаемая совокупность, тем надежнее полученная средняя.
2) Если 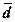 /σ < 0,8, так как это условие соблюдается можно
сделать вывод об устойчивости индивидуальных значений признака Среднегодовая стоимость основных
производственных фондов и признака выпуска
продукции, то есть среди них отсутствуют «аномальные» варианты значений,
значения признака устойчивы.
/σ < 0,8, так как это условие соблюдается можно
сделать вывод об устойчивости индивидуальных значений признака Среднегодовая стоимость основных
производственных фондов и признака выпуска
продукции, то есть среди них отсутствуют «аномальные» варианты значений,
значения признака устойчивы.
3) полученные значения процентного соотношения рассеяния для наших
признаков близки к значениям процентного соотношения признаков, распределенных
по нормальному закону, исходя из этого можно сделать вывод о том, что наше
распределение близко к к нормальному.
4) а)Vσ1< Vσ2 (Vσ1 = 16,9941 Vσ2 = 21,749) поэтому колеблемость единиц
совокупности для первого признака меньше, чем для второго.
б) количественная однородность единиц выше для второго признака по
сравнению с первым, исходя из значений показателя коэффициента вариации
в) для второго признака средняя арифметическая величина является более
надежной характеристикой чем для первого (исходя из значений показателя
коэффициента вариации)
г) поскольку x < Me < Mo
и Asп1
< 0 для первого признака характерна левосторонняя асимметрия (Asп1= -0,210).
Поскольку x
> Me
>Mo
и Asп2>0 для второго
признака характерна правосторонняя асимметрия Asп = 0,0152. Так как для обоих
признаков |As|
≤ 0,25 – асимметрия незначительная.
5) при анализе формы гистограммы прежде всего следует
оценить распределение вариантов значений признака по интервалам (группам) .