СОДЕРЖАНИЕ
Задача №1. 3
Задача №2. 5
Задача №3. 6
Задача №4. 9
Задача №5. 10
СПИСОК ЛИТЕРАТУРЫ.. 12
Вариант 7
Задача №1
Имеются данные о мощности электростанции России (на начало года, млн. КВТ):
|
Группа электростанций |
1998 год |
1999 год |
2000 год |
|
Тепловые |
188,4 |
188,8 |
189,7 |
|
Гидроэлектростанции |
48,4 |
46,4 |
48,6 |
|
Атомные |
26,2 |
27,2 |
27,2 |
|
ИТОГО: |
263,0 |
262,4 |
265,5 |
Определить: 1) Показатели динамики мощности всех электростанций России;
2) Показатели структуры мощности электростанции в 1998 году.
Решение
1. Показатели динамики характеризуют развитие изучаемого явления во времени. Они позволяют при анализе данных, характеризующих развитие явления во времени, выявлять направление развития и измерять темпы роста.
Темпы роста исчисляются как отношения абсолютных (или средних) уровней ряда и выражаются в форме коэффициентов или процентов.
Темп роста (Тр) – это соотношение последующего уровня ряда к предыдущему (цепные темпы роста) или постоянному, принятому за базу сравнения (базисные темпы роста)[1]:
Цепные коэффициенты (темпы) роста рассчитываются по формуле:
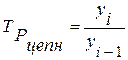 (1)
(1)
Базисные коэффициенты (темпы) роста рассчитываются по формуле:
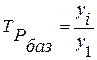 , (2)
, (2)
Составим таблицу 1.
Таблица 1
|
Показатель |
Год |
||
|
1998 год |
1999 год |
2000 год |
|
|
Общая мощность, млн. КВТ |
263,0 |
262,4 |
265,5 |
|
Темпы роста, % ─ базисные ─ цепные |
─ ─ |
262,4/263=99,8 262,4/263=99,8 |
265,5/263=100,9 265,5/262,4=101,2 |
Таким образом, мощность всех электростанций России в 1999 году по сравнению с 1998 годом снизилась на 0,2%, а в 2000 году по сравнению с 1999 годом увеличилась на 1,2% и по сравнению с базисным 1998 годом – на 0,9%.
2. Показатели структуры характеризуют долю (удельный вес) составных частей целого в их общем итоге и обычно выражаются в виде коэффициентов (доли единиц) или процентах.
При определении показателей структуры сравниваемыми величинами могут быть и численности отдельных групп статистической совокупности, или объемы их признаков. За основание (базу) сравнения принимается общий итог статистической совокупности.[2]
Для расчета показателей структуры мощности электростанции в 1998 году составим таблицу 2.
Таким образом, наибольшая доля приходится на мощность тепловых электростанций – 71,64 %, наименьшая – на мощность атомных электростанций – 9,96 %. Доля мощности гидроэлектростанций составляет 18,4 % от их общего числа.
Таблица 2
Структура мощности электростанции в 1998 году
|
Вид электростанции |
Мощность, млн. КВТ |
В % к итогу |
|
Тепловые |
188,4 |
71,64 |
|
Гидроэлектростанции |
48,4 |
18,40 |
|
Атомные |
26,2 |
9,96 |
|
ИТОГО: |
263,0 |
100,0 |
Задача №2
По данным таблицы исчислите среднюю заработную плату продавцов по магазину:
|
Группа продавцов |
Средняя месячная з/плата продавца в тыс. руб. |
Всего начислено з/платы в млн. руб. |
|
1-я |
110 |
124,0 |
|
2-я |
120 |
278,0 |
|
3-я |
135 |
135,0 |
Укажите вид средней величины, которую вы применили.
Решение
В процессе обработки и обобщения статистических данных возникает необходимость определения средних величин. Средняя величина – обобщающая характеристика изучаемого признака в исследуемой совокупности. Она отражает его типичный уровень в расчете на единицу совокупности в конкретных условиях места и времени.[3]
Так как по условию задачи отсутствуют данные о частоте появления признака, но имеется информация об общем значении признака (всей начисленной заработной платы), то для расчета средней заработной платы продавцов по магазину применяем формулу средней гармонической взвешенной:
 (3)
(3)
Таким образом, средняя заработная плата продавцов по магазину составит:
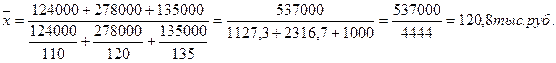
Задача №3
Для установления качества муки (% содержание клетчатки) было взято в случайном бесповоротном порядке 100 проб (15 % от всей совокупности). Результаты анализа выражаются данными, сведенными в интервальный ряд распределения:
|
% клейковины |
Число проб муки |
|
До 36,5 |
15 |
|
36,5-38,5 |
35 |
|
38,5-40,5 |
25 |
|
40,5 и выше |
25 |
|
Итого: |
100 |
Определите средний процент клейковины муки и среднее квадратическое отклонение, дисперсию, коэффициент вариации, моду и медиану.
Решение
Среднее выборочное значение определяется по формуле средней арифметической взвешенной:
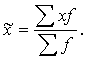 (4)
(4)
Дисперсия признака х определяется по формуле:
 (5)
(5)
Среднее квадратическое отклонение определяется по формуле:
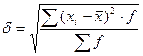 (6)
(6)
Коэффициент вариации характеризует относительную меру колеблемости и определяется по формуле:
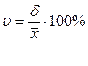 (7)
(7)
Для удобства расчетов составим вспомогательную таблицу 3
Таблица 3
|
% клейко-вины |
Число проб муки (f) |
Сере-дина интерва-ла (х) |
Накоп-ленная частота (S) |
xf |
|
( |
(х- |
|
(34,5) До 36,5 |
15 |
35,5 |
15 |
532,5 |
-3,2 |
10,24 |
153,6 |
|
36,5-38,5 |
35 |
37,5 |
50 |
1312,5 |
-1,2 |
1,44 |
50,4 |
|
38,5-40,5 |
25 |
39,5 |
75 |
987,5 |
0,8 |
0,64 |
16,0 |
|
40,5 и выше (42,5) |
25 |
41,5 |
100 |
1037,5 |
2,8 |
7,84 |
196,0 |
|
ИТОГО: |
100 |
─ |
─ |
3870,0 |
─ |
─ |
416,0 |
Средний процент клейковины составит:
![]()
Определим дисперсию среднего процента клейковины:
![]() %
%
Среднее квадратическое отклонение составит:
![]() %
%
Коэффициент вариации составит:
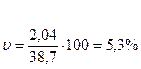
Коэффициент вариации меньше 30 %, значит, совокупность однородная и средняя – надежная.
Мода – это наиболее часто встречающееся значение признака в совокупности.[4] Модальный интервал – (36,5 – 38,5), так как ему соответствует максимальная частота, равная 35.
Мода рассчитывается по следующей формуле:
![]() (8)
(8)
где
![]() ─ нижняя граница модального интервала;
─ нижняя граница модального интервала;
fМо ─ частота в модальном интервале;
fМо-1─ частота в интервале, предшествующем модальному;
fМо+1 ─ частота в интервале, следующем за модальным;
i ─ величина интервала.
Мода составит:
![]()
Процент клейковины, равный 37,8 чаще всего встречается в совокупности.
Медиана соответствует варианту, стоящему в середине ранжированного ряда. Медианный интервал определяем по накопленной частоте, стоящей в середине совокупности. Значение 50 находится в интервале 36,5 – 38,5.
Мода рассчитывается по следующей формуле:
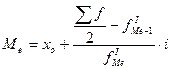 (9)
(9)
где ![]() накопленная частота
медианного интервала;
накопленная частота
медианного интервала;
![]() накопленная частота в интервале перед медианным;
накопленная частота в интервале перед медианным;
Медиана составит:
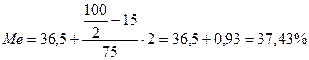
Значение 37,43 % находится в середине совокупности.
Задача №4
Имеются следующие данные о стоимости имущества предприятия (млн. руб.)
|
Год |
Отчетные данные |
|||
|
01.01 |
01.04 |
01.07 |
01.10 |
|
|
1995 |
62 |
65 |
70 |
68 |
|
1996 |
68 |
70 |
75 |
70 |
|
1997 |
80 |
84 |
88 |
90 |
|
1998 |
95 |
─ |
─ |
─ |
Определить абсолютные и относительные изменения среднегодовой стоимости имущества предприятия в 1997 году по сравнению с 1995 годом и 1996 годом.
Решение
Так как по условию даны данные о стоимости имущества предприятия на определенные даты, то этот ряд динамики является моментным.
Средний уровень моментного ряда динамики определяется по формуле средней хронологической:
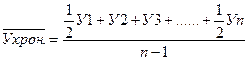 (10)
(10)
Определим среднегодовую стоимость имущества в 1995, 1996 и 1997 гг.
Среднегодовая стоимость имущества в 1995 году составит:
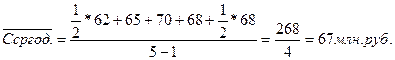
Среднегодовая стоимость имущества в 1996 году составит:

Среднегодовая стоимость имущества в 1997 году составит:
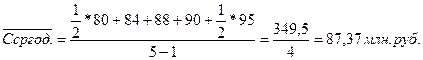
Для определения абсолютных и относительных изменений среднегодовой стоимости имущества предприятия в 1997 году по сравнению с 1995 годом и 1996 годом составим таблицу 4.
Таблица 4
Динамика среднегодовой стоимости имущества предприятия в 1995-1997 гг.
|
Показатель |
Год |
Изменение |
Год |
Изменение |
||||
|
1995 |
1997 |
Абсолют-ное, млн. руб. |
Относи-тельное, % |
1996 |
1997 |
Абсолют-ное, млн. руб. |
Относи-тельное, % |
|
|
Среднегодовая стоимость имущества, млн. руб. |
67 |
87,37 |
+20,37 |
130,4 |
74,25 |
87,37 |
+13,12 |
117,7 |
Таким образом, можно сделать следующие выводы:
Среднегодовая стоимость имущества в 1997 году увеличилась по сравнению с 1995 годом на 67 млн. руб., или на 30,4%, а по сравнению с 1996 годом – на 13,12 млн. руб., или на 17,7%.
Задача №5
Используя данные таблицы, определите:
а) общий индекс цен
б) общий индекс физического объема товарооборота
в) общий индекс фактического товарооборота
|
Товары |
Цена за |
Количество проданной продукции, тонн |
||
|
В базисном периоде |
В отчетном периоде |
В базисном периоде |
В отчетном периоде |
|
|
А |
3,0 |
5,0 |
160 |
200 |
|
Б |
2,0 |
3,8 |
200 |
220 |
|
В |
3,0 |
4,8 |
300 |
280 |
|
Итого: |
660 |
700 |
Решение
Индекс – это относительный показатель сравнения общественных явлений во времени, пространстве или в сопоставлении с планом.
Общий (сводный) индекс характеризует изменение по всей совокупности элементов сложного явления.[5]
Общий индекс цен определяется по формуле:
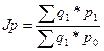 (11)
(11)
![]() , или 169 %
, или 169 %
Цены на три товара в среднем выросли на 69%.
Прирост товарооборота за счет изменения цен составил:
∑р1q1 - ∑р0q1 = 3180-1880=1300 тыс. руб.
Общий индекс физического объема товарооборота определяется по формуле:
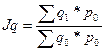 (12)
(12)
![]() , или 105,6 %
, или 105,6 %
Количество проданной продукции было в отчетном периоде больше на 5,6 %, чем в базисном периоде.
Прирост товарооборота за счет изменения количества проданных товаров составил:
∑р0q1 - ∑р0q0 = 1880-1780=100 тыс. руб.
Общий индекс фактического товарооборота определяется по формуле:
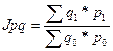 (13)
(13)
![]() , или 178,65 %
, или 178,65 %
В отчетном периоде по сравнению с базисным товарооборот увеличился на 1300 тыс. руб. за счет увеличения цен на 69 % и на 100 тыс. руб. за счет увеличения количества проданной продукции на 5,6%.
СПИСОК ЛИТЕРАТУРЫ
1. Гусаров В.М. Теория статистики. – М.: ЮНИТИ, 1998. – 448 с.
2. Елисеева И.И., Юзбашев М.М. Общая теория статистики. – М.: Финансы и статистика, 1998. – 368 с.
3. Ефимова М. Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. – М.: ИНФРА-М. 2002. – 416 с.
4. Савицкая Г. В. Анализ хозяйственной деятельности предприятия. 2-е изд., испр. и доп. – М.: ИНФРА-М. 2003. − 400 с.
5. Теория статистики / Под редакцией Шмойловой Р. А. – М.: Финансы и статистика, 2002. – 576 с.
[1] Ефимова М. Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. – М.: ИНФРА-М. 2002. – с. 289
[2] Теория статистики / Под редакцией Шмойловой Р. А. – М.: Финансы и статистика, 2002. – с. 256
[3] Ефимова М. Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. – М.: ИНФРА-М. 2002. – с. 89
[4] Гусаров В.М. Теория статистики. – М.: ЮНИТИ, 1998. – с. 149
[5] Елисеева И.И., Юзбашев М.М. Общая теория статистики. – М.: Финансы и статистика, 1998. – с. 306