ПРИЛОЖЕНИЕ 2.1
 |
КАФЕДРА СТАТИСТИКИ
О Т Ч Е Т
о результатах выполнения
компьютерной лабораторной работы №2
«Автоматизированный корреляционно-регрессионный анализ взаимосвязи статистических данных
в среде MS Excel»
Выполнил:
Проверил:
Серпухов, 2006 г.
Постановка задачи
Корреляционно-регрессионный анализ (КР-анализ) взаимосвязи признаков является составной частью проводимого статистического исследования двух экономических показателей статистической совокупности 32 предприятий и частично использует результаты Лабораторной работы №1.
В лабораторной работе №2 изучается взаимосвязь между факторным признаком Среднегодовая стоимость основных производственных фондов (признак Х) и результативным признаком Выпуск продукции (признак Y), значениями которых являются исходные данные Лабораторной работы №1 после исключения из них аномальных значений.
Таблица 2,1
Исходные данные демонстрационного примера
|
Номер предприятия |
Среднегдовая стоимость основных производственных фондов, млн руб. |
Выпуск продукции, млн руб. |
|
1 |
94,00 |
110,00 |
|
2 |
107,00 |
101,00 |
|
3 |
134,00 |
120,00 |
|
4 |
157,00 |
81,00 |
|
5 |
163,00 |
80,00 |
|
6 |
167,00 |
114,00 |
|
29 |
167,00 |
114,00 |
|
7 |
173,00 |
161,00 |
|
8 |
173,00 |
90,00 |
|
9 |
177,00 |
178,00 |
|
10 |
179,00 |
107,00 |
|
11 |
200,00 |
125,00 |
|
12 |
201,00 |
108,00 |
|
13 |
205,00 |
133,00 |
|
30 |
205,00 |
133,00 |
|
14 |
208,00 |
124,00 |
|
15 |
212,00 |
201,00 |
|
16 |
213,00 |
161,00 |
|
17 |
214,00 |
151,00 |
|
18 |
216,00 |
169,00 |
|
19 |
218,00 |
149,00 |
|
20 |
230,00 |
180,00 |
|
21 |
234,00 |
148,00 |
|
22 |
237,00 |
162,00 |
|
23 |
241,00 |
166,00 |
|
24 |
248,00 |
168,00 |
|
32 |
260,00 |
224,00 |
|
26 |
276,00 |
171,00 |
|
27 |
290,00 |
191,00 |
|
28 |
298,00 |
220,00 |
В процессе статистического исследования необходимо решить ряд задач.
1.Установить наличие статистической связи между факторным признаком Х и результативным Y:
a) Графическим методом;
b) Методом сопоставления параллельных рядов.
2.Установить наличие корреляционной связи между признаками Х и Y методом аналитической группировки.
3.Оценить тесноту связи признаков Х и Y на основе:
a) Эмпирического корреляционного отношения η;
b) Линейного коэффициента корреляции r.
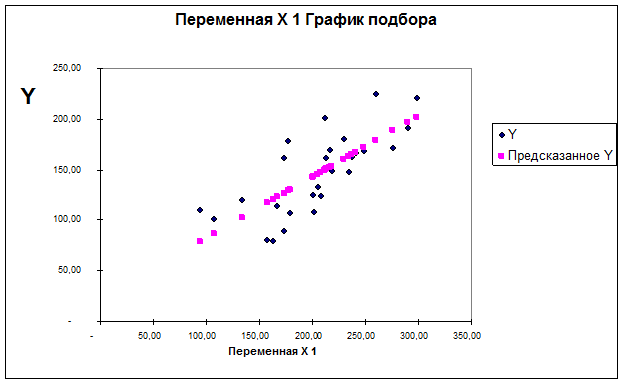
4.Построить однофакторную линейную регрессионную модель связи признаков Х и Y, используя инструмент регрессия надстройки Пакет анализа.
5. Оценить адекватность и практическую пригодность построенной линейной регрессионной модели, указав:
а) Доверительные интервалы коэффициентов ![]() ;
;
б) Степень тесноты связи признаков Х и Y;
в) Погрешность регрессионной модели.
6) Дать экономическую интерпретацию:
а) Коэффициента регрессии ![]() ;
;
б) Коэффициента эластичности ![]() ;
;
в) Остаточных величин ![]() .
.
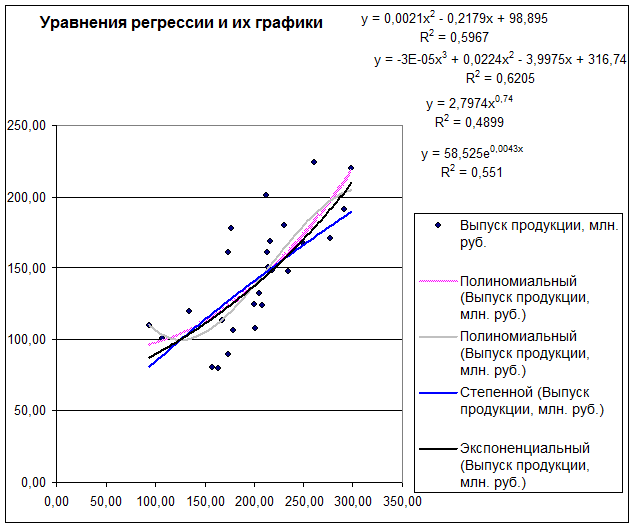
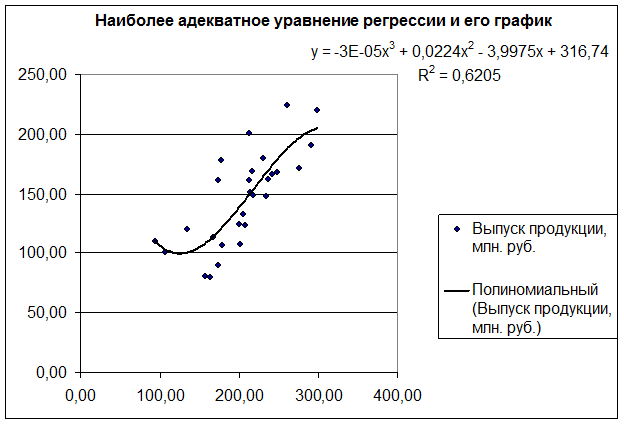
7. Найти наиболее адекватное нелинейное уравнение регрессии с помощью средств инструмента Мастер диаграмм. Построить для этого уравнения теоретическую кривую регрессии.
|
Таблица 2,2 |
||||
|
Зависимость выпуска продукции от среднегодовой стоимости основных фондов |
||||
|
Номер группы |
Группы предприятий по стоимости основных фондов |
Число предприятий |
Выпуск продукции |
|
|
Всего |
В среднем на одно предприятие |
|||
|
1 |
94-134 |
3 |
331,00 |
110,33333 |
|
2 |
157-173 |
6 |
640,00 |
106,66667 |
|
3 |
177--216 |
11 |
1 590,00 |
144,54545 |
|
4 |
218-248 |
6 |
973,00 |
162,16667 |
|
5 |
260-298 |
4 |
806,00 |
201,5 |
|
Итого |
|
30 |
4 340,00 |
144,66667 |
|
Таблица 2,3 |
|||
|
Показатели внутригрупповой вариации |
|||
|
Номер группы |
Группы предприятий по стоимости основных фондов |
Число предприятий |
Внутригрупповая дисперсия |
|
1 |
94-134 |
3 |
60,2222222 |
|
2 |
157-173 |
6 |
784,555556 |
|
3 |
177--216 |
11 |
821,157025 |
|
4 |
218-248 |
6 |
123,472222 |
|
5 |
260-298 |
4 |
472,25 |
|
Итого |
|
30 |
2261,65702 |
|
Таблица 2,4 |
|||
|
Показатели дисперсии и эмпирического корреляционного отношения |
|||
|
Общая дисперсия |
Средняя из внутригрупповых дисперсий |
Межгрупповая дисперсия |
Эмпирическое корреляционное отношение |
|
1450,288889 |
551,6853535 |
898,6035354 |
0,78714873 |
|
Таблица 2,5 |
||
|
Линейный коэффициент корреляции признаков |
||
|
|
Столбец 1 |
Столбец 2 |
|
Столбец 1 |
1 |
|
|
Столбец 2 |
0,753661673 |
1 |
|
ВЫВОД ИТОГОВ |
|
|
Регрессионная статистика |
|
|
Множественный R |
0,753662 |
|
R-квадрат |
0,568006 |
|
Нормированный R-квадрат |
0,552578 |
|
Стандартная ошибка |
25,90883 |
|
Наблюдения |
30 |
|
Дисперсионный анализ |
|||||
|
|
df |
SS |
MS |
F |
Значимость F |
|
Регрессия |
1 |
24713,18 |
24713,18 |
36,8157 |
1,52606E-06 |
|
Остаток |
28 |
18795,49 |
671,2674 |
||
|
Итого |
29 |
43508,67 |
|
|
|
|
|
Коэффи- циенты |
Стан- дарт- ная ошибка |
t- ста-тистика |
P- Значение |
Нижние 95% |
Верхние 95% |
Нижние 68,3% |
Верхние 68,3% |
|
Y-пере-сечение |
21,64455 |
20,81975 |
1,039616 |
0,307413 |
-21,0028316 |
64,2919 |
0,43246 |
42,8566 |
|
Перемен-ная X 1 |
0,605325 |
0,099764 |
6,067594 |
1,53E-06 |
0,400967996 |
0,80968 |
0,50368 |
0,70697 |
|
ВЫВОД ОСТАТКА |
|
Наблюдение |
Предсказанное Y |
Остатки |
|
1 |
78,54505 |
31,45495 |
|
2 |
86,41427 |
14,58573 |
|
3 |
102,758 |
17,24197 |
|
4 |
116,6805 |
-35,6805 |
|
5 |
120,3124 |
-40,31244 |
|
6 |
122,7337 |
-8,733742 |
|
7 |
122,7337 |
-8,733742 |
|
8 |
126,3657 |
34,63431 |
|
9 |
126,3657 |
-36,36569 |
|
10 |
128,787 |
49,21301 |
|
11 |
129,9976 |
-22,99764 |
|
12 |
142,7095 |
-17,70945 |
|
13 |
143,3148 |
-35,31478 |
|
14 |
145,7361 |
-12,73607 |
|
15 |
145,7361 |
-12,73607 |
|
16 |
147,552 |
-23,55205 |
|
17 |
149,9733 |
51,02666 |
|
18 |
150,5787 |
10,42133 |
|
19 |
151,184 |
-0,183994 |
|
20 |
152,3946 |
16,60536 |
|
21 |
153,6053 |
-4,605292 |
|
22 |
160,8692 |
19,13081 |
|
23 |
163,2905 |
-15,29048 |
|
24 |
165,1065 |
-3,106458 |
|
25 |
167,5278 |
-1,527756 |
|
26 |
171,765 |
-3,765027 |
|
27 |
179,0289 |
44,97108 |
|
28 |
188,7141 |
-17,71411 |
|
29 |
197,1887 |
-6,188656 |
|
30 |
202,0313 |
17,96875 |