ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ
ИНСТИТУТ
КАФЕДРА СТАТИСТИКИ
О Т Ч Е Т
о результатах выполнения
компьютерной лабораторной
работы №2
Автоматизированный корреляционно-регрессионный
анализ взаимосвязи статистических данных в среде MS Excel
Вариант № 37
Выполнила: ст. III курса гр.2
Стешина О.С.
Специальность
ГМУ
№
личного дела 05МГД48037
Проверила:
Вдовина И.В.
Брянск, 2006 г.
1. Постановка задачи
Корреляционно-регрессионный
анализ взаимосвязи признаков является составной частью проводимого
статистического исследования и частично использует результаты Лабораторной
работы № 1.
В Лабораторной работе № 2
изучается взаимосвязь между факторным признаком Среднегодовая стоимость основных производственных фондов (признак Х) и результативным признаком Выпуск продукции (признак Y), значениями которых являются исходные данные
Лабораторной работы № 1 после исключения из них аномальных значений.
|
|
|
Таблица
2.1
|
|
Исходные
данные
|
|
Номер
предприятия
|
Среднегодовая
стоимость основных производственных фондов, млн.руб.
|
Выпуск
продукции, млн. руб.
|
|
5
|
1745,00
|
1365,00
|
|
23
|
1881,50
|
1813,50
|
|
27
|
2037,50
|
1560,00
|
|
1
|
2096,00
|
2008,50
|
|
8
|
2174,00
|
2145,00
|
|
32
|
2213,00
|
2262,00
|
|
22
|
2369,00
|
1930,50
|
|
19
|
2427,50
|
1852,50
|
|
2
|
2466,50
|
2203,50
|
|
3
|
2544,50
|
2457,00
|
|
13
|
2564,00
|
2613,00
|
|
26
|
2622,50
|
2398,50
|
|
9
|
2661,50
|
2515,50
|
|
4
|
2681,00
|
2730,00
|
|
28
|
2739,50
|
2437,50
|
|
17
|
2759,00
|
2496,00
|
|
6
|
2817,50
|
2340,00
|
|
14
|
2817,50
|
2847,00
|
|
25
|
2817,50
|
2535,00
|
|
7
|
2895,50
|
3159,00
|
|
30
|
3012,50
|
2535,00
|
|
18
|
3051,50
|
2964,00
|
|
10
|
3071,00
|
3139,50
|
|
20
|
3090,50
|
2535,00
|
|
24
|
3149,00
|
2905,50
|
|
29
|
3168,50
|
2671,50
|
|
15
|
3227,00
|
3451,50
|
|
11
|
3363,50
|
3315,00
|
|
21
|
3441,50
|
3412,50
|
|
16
|
3695,00
|
3705,00
|
В процессе
статистического исследования необходимо решить ряд задач.
1. Установить
наличие стохастической связи между факторным признаком Х и результативным признаком Y:
а) графическим методом;
б) методом сопоставления параллельных рядов.
2. Установить
наличие корреляционной связи между признаками Х и Y методом аналитической группировки.
3.
Оценить
тесноту связи признаков Х и Y на основе:
а) эмпирического корреляционного отношения η;
б) линейного коэффициента корреляции r.
Сравнить
значения η и r и сделать
вывод о возможности линейной связи между признаками Х и Y.
4.
Построить однофакторную линейную регрессионную модель
связи признаков Х и Y, используя инструмент Регрессия надстройки Пакет анализа, и рассчитать
доверительные интервалы коэффициентов уравнения линейной регрессии.
Построить
теоретическую кривую регрессии.
Дать
экономическую интерпретацию коэффициента регрессии.
Рассчитать коэффициент эластичности и дать его
экономическую интерпретацию.
5. Найти
наиболее адекватное уравнение регрессии с помощью средств инструмента Мастер диаграмм.
II.
Рабочий файл с результативными таблицами и графиками.
|
|
|
|
|
Таблица
2.2
|
|
Зависимость
выпуска продукции от среднегодовой стоимости основных фондов
|
|
Номер
группы
|
Группы
предприятий по стоимости основеных фондов
|
Число
предприятий
|
Выпуск
продукции
|
|
Всего
|
В
среднем
на одно
предприятие
|
|
1
|
1745-2135
|
4
|
6747,00
|
1686,75
|
|
2
|
2135-2525
|
5
|
10393,50
|
2078,70
|
|
3
|
2525-2915
|
11
|
28528,50
|
2593,50
|
|
4
|
2915-3305
|
7
|
20202,00
|
2886,00
|
|
5
|
3305-3695
|
3
|
10432,50
|
3477,50
|
|
Итого
|
|
30
|
76303,50
|
2543,45
|
|
|
|
|
Таблица
2.3
|
|
Показатели внутригрупповой
вариации
|
|
|
|
Номер
группы
|
Группы
предприятий по стоимости основеных фондов
|
Число
предприятий
|
Внутригрупповая
дисперсия
|
|
1
|
1745-2135
|
4
|
55342,23
|
|
2
|
2135-2525
|
5
|
35226,30
|
|
3
|
2525-2915
|
11
|
35734,15
|
|
4
|
2915-3305
|
7
|
63714,79
|
|
5
|
3305-3695
|
3
|
23871,06
|
|
Итого
|
|
30
|
213888,54
|
|
|
|
|
Таблица
2.4
|
|
|
Показатели дисперсии и
эмпирического корреляционного отношения
|
|
|
|
Общая
дисперсия
|
Средняя
из внутригрупповых дисперсия
|
Межгрупповая
дисперсия
|
Эмпирическое
корреляционное отношение
|
|
|
306017,1725
|
43606,4275
|
262410,745
|
0,926014758
|
|
|
Таблица 2.5
|
|
|
|
|
Столбец
1
|
Столбец
2
|
|
|
|
Столбец 1
|
1
|
|
|
|
|
Столбец 2
|
0,91318826
|
1
|
|
|
|
Таблица
2.6
|
|
|
|
|
|
|
ВЫВОД ИТОГОВ
|
|
|
|
|
|
|
|
|
|
Регрессионная
статистика
|
|
|
|
Множественный R
|
0,91318826
|
|
|
|
R-квадрат
|
0,833912798
|
|
|
|
Нормированный R-квадрат
|
0,827981112
|
|
|
|
Стандартная ошибка
|
233,3579468
|
|
|
|
Наблюдения
|
30
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица
2.8
|
Дисперсионный анализ
|
df
|
SS
|
MS
|
F
|
Значимость
F
|
|
Регрессия
|
1
|
7655749,098
|
7655749,098
|
140,5861384
|
1,97601E-12
|
|
Остаток
|
28
|
1524766,077
|
54455,93131
|
|
|
|
Итого
|
29
|
9180515,175
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
Нижние
95%
|
|
Y-пересечение
|
-419,5960922
|
253,5063443
|
-1,655169986
|
0,109057642
|
-938,8802914
|
|
Переменная X 1
|
1,089355181
|
0,09187519
|
11,85690257
|
1,97601E-12
|
0,901157387
|
Таблица
2.9
|
ВЫВОД ОСТАТКА
|
|
|
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
|
1
|
1481,328699
|
-116,3286986
|
|
2
|
1630,025681
|
183,4743192
|
|
3
|
1799,965089
|
-239,965089
|
|
4
|
1863,692367
|
144,8076329
|
|
5
|
1948,662071
|
196,3379288
|
|
6
|
1991,146923
|
270,8530767
|
|
7
|
2161,086331
|
-230,5863315
|
|
8
|
2224,81361
|
-372,3136096
|
|
9
|
2267,298462
|
-63,79846163
|
|
10
|
2352,268166
|
104,7318343
|
|
11
|
2373,510592
|
239,4894082
|
|
12
|
2437,23787
|
-38,73786986
|
|
13
|
2479,722722
|
35,77727809
|
|
14
|
2500,965148
|
229,0348521
|
|
15
|
2564,692426
|
-127,192426
|
|
16
|
2585,934852
|
-89,93485206
|
|
17
|
2649,66213
|
-309,6621301
|
|
18
|
2649,66213
|
197,3378699
|
|
19
|
2649,66213
|
-114,6621301
|
|
20
|
2734,631834
|
424,3681657
|
|
21
|
2862,08639
|
-327,0863904
|
|
22
|
2904,571242
|
59,42875752
|
|
23
|
2925,813669
|
213,6863315
|
|
24
|
2947,056095
|
-412,0560945
|
|
25
|
3010,783373
|
-105,2833726
|
|
26
|
3032,025799
|
-360,5257987
|
|
27
|
3095,753077
|
355,7469233
|
|
28
|
3244,450059
|
70,54994106
|
|
29
|
3329,419763
|
83,08023694
|
|
30
|
3605,571301
|
99,42869857
|
|
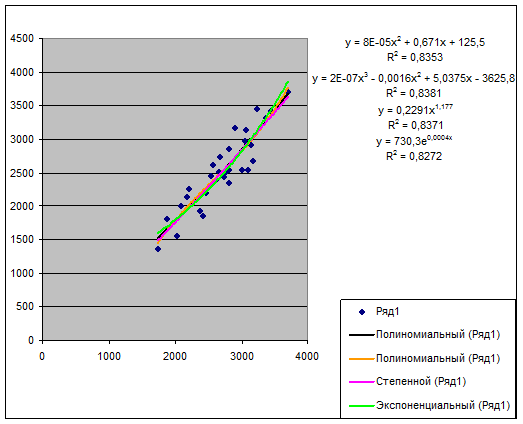
Диаграмма 2.1–ДП
Уравнения регрессии и их графики
|
|
Диаграмма 2.2–ДП
Наиболее адекватное уравнение
регрессии и его график 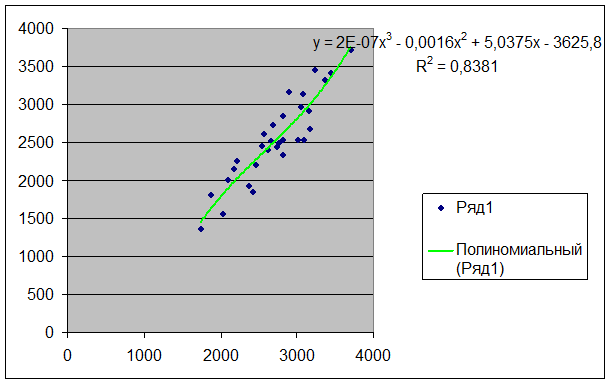
|
III.
Выводы по результатам выполнения лабораторной работы.
Задача 1.
Установление наличия стохастической связи между факторным
признаком Х и результативным
признаком Y:
а)
графическим методом.
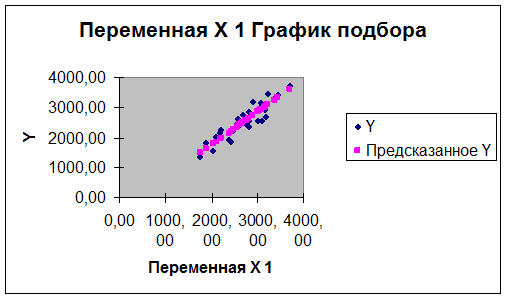
Вывод: На основе
анализа диаграммы рассеяния из Лабораторной
работы №1, полученной после удаления аномальных значений, можно сделать
вывод, что имеет место стохастическая
связь. Предположительный вид связи: линейная, прямая.
б) методом
сопоставления параллельных рядов.
Вывод: Табл.2.1, полученная путем ранжирования
предприятий по возрастанию значения факторного признака Х, показывает, что с увеличением значений факторного признака
увеличиваются значения результативного
признака, за исключением некоторых отклонений, что позволяет сделать вывод о в
целом существующей связи между стоимостью основных фондов и выпуском продукции
Задача 2.
Установление наличия корреляционной связи между признаками Х и Y методом аналитической группировки.
Вывод:
Результаты выполнения
аналитической группировки предприятий по факторному признаку Среднегодовая стоимость основных
производственных фондов даны в табл. 2.2 Рабочего файла, которая
показывает, что происходит увеличение выпуска продукции с увеличением стоимости основных фондов.
Причем зависимость является прямой зависимостью, оптимальной по
стоимости является группа со стоимостью основных фондов в диапазоне 3305-3695 тыс. руб. Тем не менее, число предприятий
с данной величиной основных фондов самое малочисленное и составляет 3 предприятия. Наиболее многочисленной является группа предприятий со стоимостью основных фондов в диапазоне 2525-2915
тыс. руб., которая составляет 11
предприятий.
Задача
3.Оценка тесноты связи признаков Х и Y:
а) на основе
эмпирического корреляционного отношения
Для анализа
тесноты связи между факторным и результативным признаками, рассчитывается
показатель η - эмпирическое
корреляционное отношение, задаваемое формулой
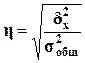
Для
вычисления η необходимо знать общую дисперсию 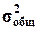 и межгрупповую
дисперсию
и межгрупповую
дисперсию 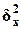 результативного
признака Y - Выпуск продукции.
результативного
признака Y - Выпуск продукции.
Результаты выполненных расчетов представляются табл.
2.4 Рабочего файла.
Вывод: Величина η=0,926014758
является близкой к единице, что свидетельствует о прямой связи между анализируемыми факторами
при которой с увеличением среднегодовой
стоимости основных фондов увеличивается выпуск продукции.
б)
на основе линейного коэффициента
корреляции признаков
В
предположении, что связь между факторным и результативным признаком имеется,
для определения тесноты связи на основе линейного коэффициента корреляции r был
использован инструмент Корреляция
надстройки Пакет анализа.
Результатом
работы инструмента Корреляции
является табл. 2.5 Рабочего файла.
Вывод: Значение
коэффициента корреляции r=0,91318826 лежит в интервале 0< r <1, что в соответствии со шкалой Чэддока, говорит
о наличии прямой связи между анализируемыми факторным и результативным признаками
Так как значение коэффициента
корреляции r положительное, то связь между признаками прямая.
Посредством показателя η измеряется теснота связи любой формы, а с помощью
коэффициента корреляции r – только прямолинейная, следовательно, значения η и r совпадают
только при наличии прямолинейной связи. В теории статистики установлено, что
если 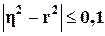 , то гипотезу о прямолинейной связи можно считать
подтвержденной.
, то гипотезу о прямолинейной связи можно считать
подтвержденной.
Вывод: так как 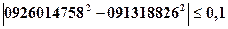 002 < r <1 то гипотезу о прямолинейной связи между основными
фондами и выпуском продукции можно считать подтвержденной.
002 < r <1 то гипотезу о прямолинейной связи между основными
фондами и выпуском продукции можно считать подтвержденной.
Задача 4. Построение однофакторной линейной
регрессионной модели связи изучаемых признаков с помощью инструмента Регрессия
надстройки Пакет анализа.
Построение
регрессионной модели заключается в определении аналитического выражения связи
между факторным признаком X
и результативным признаком Y.
Инструмент
Регрессия производит расчет
параметров а0 и а1 уравнения однофакторной
линейной регрессии 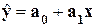 и проверка его адекватности исследуемым
фактическим данным.
и проверка его адекватности исследуемым
фактическим данным.
В
результате работы инструмента Регрессия
были получены результативные таблицы 2.6 – 2.9 Рабочего файла.
Вывод: Однофакторная линейная регрессионная модель связи
факторного и результативного признаков имеет вид 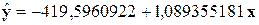
Доверительные интервал коэффициентов уравнения
регрессии представим в нижеследующей таблице
|
Коэффициенты
|
Границы доверительных
интервалов
|
|
С надежностью Р=0,68
|
С надежностью Р=0,95
|
|
Нижние
|
Верхние
|
Нижние
|
Верхние
|
|
а0
|
-677,8795819
|
-161,3126025
|
-938,8802914
|
99,688107
|
|
а1
|
0,995748668
|
1,182961694
|
0,901157387
|
1,277552975
|
С увеличением надежности границы
доверительных интервалов становятся выше.
Экономическая
интерпретация коэффициента регрессии а1:
данный параметр выражает начальную скорость роста явления, т.е. взаимосвязи
между основными фондами и выпуском
продукции.
Коэффициент эластичности 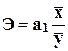 = 1,089355181 * -
= 1,089355181 * -
Экономическая
интерпретация коэффициента эластичности Э:
Коэффициент эластичности показывает, насколько процентов в среднем изменится значение
результативного признака при изменении факторного признака на 1%.
Задача 5. Нахождение
наиболее адекватного уравнения регрессии с помощью средств инструмента Мастер диаграмм. Построение для этого
уравнения теоретической линии регрессии.
Возможности инструмента Мастер диаграмм позволяют быстро
производить построение и анализ адекватности регрессионных моделей,
базирующихся на использовании различных видов зависимости между признаками X и Y.
Построение моделей осуществляется
непосредственно на диаграмме рассеяния.
На диаграмме рассеяния отображается
линия и уравнение регрессии, а также коэффициент детерминации R2.
В
лабораторной работе уравнения регрессии и их графики были построены для 5-ти
видов зависимости между признаками и даны на диаграмме Диаграмма 2.1–ДП
Уравнения регрессии и их графики Рабочего файла.
Уравнения регрессии и
соответствующие им коэффициент детерминации R2 даны в следующей таблице:
Регрессионные
модели связи[1]
|
Вид уравнения
|
Уравнение регрессии
|
Коэффициент
детерминации R2
|
|
Линейное
|
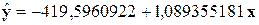
|
0,8339
|
|
Полином 2-го порядка
|
У=8E-05х2 +0,671х+125,5
|
0,8353
|
|
Полином 3-го порядка
|
У=2E-07х3 +0,0016х2+5,0375х-3625,8
|
0,8381
|
|
Степенное
|
У=0,2291х1,177
|
0,8371
|
|
Экспоненциальное
|
У=730,3е0,0004х
|
0,8372
|
Выбор наиболее адекватного
уравнения регрессии определяется максимальным значением коэффициента
детерминации R2: чем ближе
значение R2
к единице, тем более точно регрессионная модель соответствует фактическим
данным
Вывод: Максимальное
значение коэффициента детерминации R2 =0,8381
Вид
искомого уравнения регрессии – У=2E-07х3 +0,0016х2+5,0375х-3625,8
Это уравнение регрессии и его график
приведены на отдельной диаграмме рассеяния Диаграмма 2.2–ДП Наиболее адекватное
уравнение регрессии и его график Рабочего файла.
Вместе с тем, так как значения
коэффициентов R2 кубического и линейного уравнения расходятся
очень незначительно (на величину 0,004187202 (0,8381 - 0,833912798), а для показателей тесноты
связи имеет место неравенство 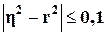 , то в качестве адекватного уравнения регрессии может быть
принято линейное уравнение
, то в качестве адекватного уравнения регрессии может быть
принято линейное уравнение 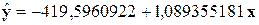 , совпадающее с
найденным с помощью инструмента Регрессия надстройки Пакет анализа.
, совпадающее с
найденным с помощью инструмента Регрессия надстройки Пакет анализа.
[1] Коэффициенты уравнений необходимо задавать не
в компьютерном формате, а в общепринятой десятичной форме чисел.