КАФЕДРА СТАТИСТИКИ

О Т Ч Е Т

о результатах выполнения

компьютерной лабораторной работы №2

«Автоматизированный корреляционно-регрессионный анализ взаимосвязи статистических данных   в среде MS Excel»

Вариант № 21

Архангельск, 2007

Постановка задачи

При проведении статистического наблюдения за деятельностью предприятий корпорации получены выборочные данные по 32-м предприятиям, выпускающим однородную продукцию  (выборка 10%-ная, механическая), о среднегодовой стоимости основных производственных фондов и  о выпуске продукции за год.

В лабораторной работе изучается взаимосвязь между факторным признаком «среднегодовая стоимость  основных производственных фондов» (признак Х) и результативным признаком «выпуск продукции» (признак У), значениями которых являются исходные данные Лабораторной работы №1 после исключения из них аномальных значений.

В процессе статистического исследования необходимо решить ряд задач:

1. Установить наличие статистической связи между факторным признаком Х и результативным признаком Y:

а) графическим методом;

б) методом сопоставления параллельных рядов.

2. Установить наличие корреляционной связи между признаками Х и Y методом аналитической группировки.

3. Оценить тесноту связи признаков Х и Y на основе:

а) эмпирического корреляционного отношения η;

б) линейного коэффициента корреляции r.

4. Построить однофакторную линейную регрессионную модель связи признаков Х и Y, используя инструмент Регрессия надстройки Пакет анализа.

5. Оценить адекватность и практическую пригодность построенной линейной регрессионной модели, указав:

а) доверительные интервалы коэффициентов ;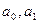

б) степень тесноты связи признаков Х и Y;

в) погрешность регрессионной модели.

6. Дать экономическую интерпретацию:

а) коэффициента регрессии ;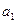

б) коэффициента эластичности ;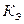

в) остаточных величин .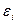

7. Найти наиболее адекватное нелинейное уравнение регрессии с помощью средств инструмента Мастер диаграмм. Построить для этого уравнения теоретическую кривую регрессии.

РЕШЕНИЕ

Задание 1

а) графический метод:

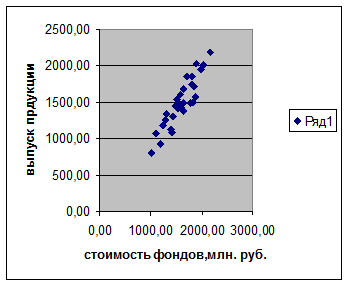
Рис. 1. Поле корреляции

       По характеру расположения точек корреляционного поля можно сделать вывод о наличии линейной прямой связи между признаками «среднегодовая стоимость  основных производственных фондов» (признак Х) и «выпуск продукции» (признак У).

б) метод сопоставления параллельных рядов.

 Ранжируем единицы совокупности по возрастанию факторного признака («Среднегодовая стоимость ОПФ»).

       С возрастанием значений признака «среднегодовая стоимость ОПФ» значения признака «выпуск продукции» в целом возрастают, между признаками Х и У возможно наличие прямой корреляционной связи.

Задание 2

       Сформируем группировку единиц совокупности по факторному признаку «среднегодовая стоимость ОПФ».

       При переходе от одной группе к другой средние значения результативного признака «выпуск продукции» возрастают, следовательно, между признаками Х и У корреляционная связь.

Задание 3

       а) Для анализа тесноты связи между факторным и результативным признаками рассчитаем показатель η – эмпирическое корреляционное отношение: .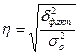

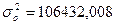: общая дисперсия характеризует всю вариацию выпуска продукции, которая возникает из стоимости ОПФ и других неучтенных при построении признаков. Рассчитывается по правилу сложения дисперсий: .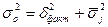

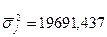: средняя из внутригрупповых дисперсий характеризует вариацию выпуска продукции, которая возникает под воздействием всех других признаков, кроме стоимости ОПФ.

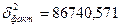: межгрупповая дисперсия характеризует вариацию выпуска продукции, которая возникает под влиянием стоимости ОФ.

Эмпирический коэффициент детерминации: η² = 0,815 или 81,5%. 81,5% вариации выпуска продукции вызывает среднегодовая стоимость ОПФ, а остальные 18,5% вариации признака вызывают другие неучтенные факторы.

Эмпирическое корреляционное отношение: η = 0,903, показывает, что связь между выпуском продукции и стоимостью ОПФ тесная.

Таблица 3 – Расчет внутригрупповых дисперсий

б) линейный коэффициент корреляции (или множественный R) равный 0,913 говорит о том, что связь между признаками есть, линейная и тесная.

Коэффициент детерминации (R²) равен 0,8339.

Нормированный R-квадрат –скорректированный коэффициент детерминации  ( более точный).

Стандартная ошибка показывает на сколько единиц в среднем расчетные значения отличается от фактических.

Цифра наблюдений говорит о том, что мы рассматривали 30 предприятий.

Таблица 5 - Линейный коэффициент корреляции признаков

Таблица 6 - Регрессионная статистика

Задание 4

Таблица 7 – Дисперсионный анализ

df- число степеней свободы, соответствует количеству факторов в модели;

SS-сумма квадратов отклонений;

MS-дисперсия факторная и остаточная;

F – расчетный критерий Фишера, равен 140,58614. Данное значение сравнивают с табличным (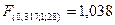), следовательно, уравнение значимо с вероятностью 0,683.

Значимость F – так как данный показатель меньше уровня значимости (0,317), то уравнение регрессии значимо с вероятностью 0,683, т. е. зависимость между признаками Х и Y регрессионной модели является статистически значимой, построенная регрессионная модель в целом адекватна исследуемому признаку.

У – пересечение: свободный член регрессии (а0), равен -242,99.

Коэффициент регрессии (а1) равен 1,089.

Стандартная ошибка – указаны значения средних квадратических отклонений для a0 u a1.

Sа0=109,992 иSа1=0,092

t-статистика –содержит расчетные значения критерия Стьюдента для проверки значимости параметров уравнения регрессии

ta0 = -1,629, ta1 = 11,857, t(0,317;28) = 1,019.

Ta1 > t(табл), следовательно, коэффициент регрессии  а1 – значим.

Р-значение (вероятность): 0,114 < 0,317, следовательно, коэффициент регрессии является значимыми, не равен нулю.

Линейное уравнение регрессии: Y= -242,99 + 1,089·Х

Задание 5

а) Интервальная оценка параметров:

С вероятностью 0,95 можно гарантировать, что а0 находится в пределах от     -548,469 до  62,499 и с  вероятностью 0,683 – а0 находится в пределах от        -394,927 до -91,042.

С вероятностью 0,95 можно гарантировать, что а1 находится в пределах от 0,901 до  1,277 и с   вероятностью 0,683 –  а1 находится в пределах от 0,996 до 1,183.

б) Коэффициент детерминации (R²) равен 0,8339 означает высокую степень тесноты связи признаков в уравнении регрессии: 83,4% вариации признака «выпуск продукции» происходит за счет фактора «среднегодовая стоимость ОПФ», включенного в модель, а остальные 16,6%  вариаций –  под влиянием факторов неучтенных в модели.

в) Погрешность регрессионной модели равна 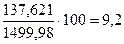%, следовательно, погрешность не большая, тогда уравнение адекватное.

Задание 6

а) Коэффициент регрессии (а1) равен 1,089: связь между результативным признаком и факторным – прямая, если факторный (Среднегодовая стоимость ОПФ) признак увеличиться на 1 млн. руб., результативный признак (выпуск продукции) в среднем увеличиться на 1,089 млн. руб. Коэффициент эластичности: 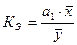, 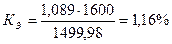. При изменении факторного признака на 1% результативный признак в среднем изменяется на 1,16%.

в)  Согласно уравнению регрессии Y = 1,089·Х-242,99 предсказанный выпуск продукции будет следующим:

Таблица 8 – Вывод остатков

Таблица 8 (продолжение)

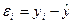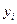Остатки: , характеризуют отклонения i-х наблюдений от расчетных значений . На предприятии №7 значение остатка максимально (250,27 млн. руб.), следовательно на данном предприятии ОПФ используются эффективнее; предприятие №20 недоиспользует ОПФ (значение остатка минимально: -243,01 млн. руб.)

Задание 7

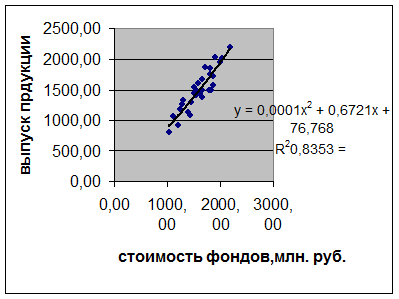
Рис.2. Уравнение регрессии (полином 2-го порядка) и его график

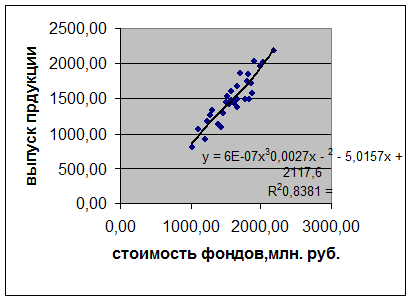
Рис. 3. Уравнение регрессии (полином 3-го порядка) и его график

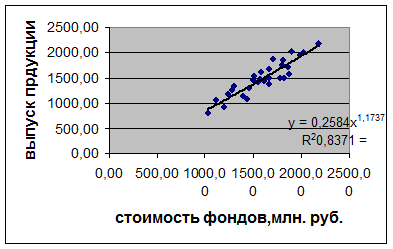
Рис. 4. Уравнение регрессии (степенная функция) и его график

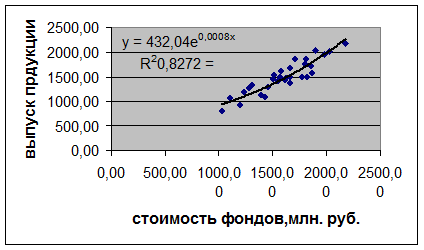
Рис. 5. Уравнения регрессии (экспонента) и его график

Максимальное значение коэффициента детерминации R² определяет вид наиболее адекватного уравнения регрессии. Таким образом, наиболее адекватная модель регрессии – полином 3-го порядка (Рис. 3).