ВСЕРОССИЙСКИЙ
ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА
СТАТИСТИКИ
О
Т Ч Е Т
о результатах выполнения
компьютерной лабораторной работы №2
Автоматизированный корреляционно-регрессионный анализ
взаимосвязи статистических данных в среде MS Excel
Вариант №2
УФА,
2006 г.
1. Постановка задачи
Корреляционно-регрессионный
анализ взаимосвязи признаков является составной частью проводимого
статистического исследования и частично использует результаты Лабораторной
работы № 1.
В Лабораторной работе № 2
изучается взаимосвязь между факторным признаком Среднегодовая стоимость основных производственных фондов (признак Х) и результативным признаком Выпуск продукции (признак Y), значениями которых
являются исходные данные Лабораторной работы № 1 после исключения из них
аномальных значений.
Таблица 2.1
|
Номер предприятия
|
Среднегодовая
стоимость основных производственных фондов, млн.руб.
|
Выпуск продукции, млн. руб.
|
|
5
|
170,00
|
140,00
|
|
23
|
184,00
|
186,00
|
|
27
|
200,00
|
160,00
|
|
1
|
206,00
|
206,00
|
|
8
|
214,00
|
220,00
|
|
32
|
218,00
|
232,00
|
|
22
|
234,00
|
198,00
|
|
19
|
240,00
|
190,00
|
|
2
|
244,00
|
226,00
|
|
3
|
252,00
|
252,00
|
|
13
|
254,00
|
268,00
|
|
26
|
260,00
|
246,00
|
|
9
|
264,00
|
258,00
|
|
4
|
266,00
|
280,00
|
|
28
|
272,00
|
250,00
|
|
17
|
274,00
|
256,00
|
|
6
|
280,00
|
240,00
|
|
14
|
280,00
|
292,00
|
|
25
|
280,00
|
260,00
|
|
7
|
288,00
|
324,00
|
|
30
|
300,00
|
260,00
|
|
18
|
304,00
|
304,00
|
|
10
|
306,00
|
322,00
|
|
20
|
308,00
|
260,00
|
|
24
|
314,00
|
298,00
|
|
29
|
316,00
|
274,00
|
|
15
|
322,00
|
354,00
|
|
11
|
336,00
|
340,00
|
|
21
|
344,00
|
350,00
|
|
16
|
370,00
|
380,00
|
В процессе статистического исследования
необходимо решить ряд задач.
1. Установить наличие стохастической
связи между факторным признаком Х
и результативным признаком Y:
а) графическим методом;
б) методом сопоставления параллельных рядов.
2. Установить наличие корреляционной
связи между признаками Х и Y методом аналитической группировки.
3. Оценить тесноту связи
признаков Х и Y на основе:
а) эмпирического корреляционного отношения η;
б) линейного коэффициента корреляции r.
Сравнить значения η и r и сделать вывод о возможности линейной связи между
признаками Х и Y.
4. Построить однофакторную
линейную регрессионную модель связи признаков Х и Y, используя
инструмент Регрессия надстройки Пакет анализ, и рассчитать
доверительные интервалы коэффициентов уравнения линейной регрессии.
5. Найти наиболее адекватное
уравнение регрессии с помощью средств инструмента Мастер диаграмм
II. Рабочего файл с результативными
таблицами и графиками.
Таблица2.2
Зависимость выпуска продукции от среднегодовой
стоимости основных фондов
|
номер группы
|
группы предприятий по
среднегодовой стоимости основных фондов, млн.руб.
|
число предприятий
|
выпуск продукции, млн.руб.
|
|
всего
|
в среднем на одно предприятие
|
|
1
|
170-210
|
4
|
692,00
|
173,00
|
|
2
|
210-250
|
5
|
1066,00
|
213,20
|
|
3
|
250-290
|
11
|
2926,00
|
266,00
|
|
4
|
290-330
|
7
|
2072,00
|
296,00
|
|
5
|
330-370
|
3
|
1070,00
|
356,67
|
|
|
|
30
|
7826,00
|
260,87
|
Таблица 2.3
Показатели внутригрупповой вариации
|
номер группы
|
Группа предприятий по стоимости
основных фондов, млн.руб.
|
Число предприятий
|
Внутригрупповые дисперсии
признака Y
|
|
1
|
170-210
|
4
|
629,0000
|
|
2
|
210-250
|
5
|
266,5600
|
|
3
|
250-290
|
11
|
542,5455
|
|
4
|
290-330
|
7
|
1026,2857
|
|
5
|
330-370
|
3
|
288,8889
|
|
|
|
30
|
2753,2801
|
Таблица 2.4
Показатели дисперсии и эмпирического корреляционного
отношения
|
Общая дисперсия
|
Дисперсия средняя из
внутригрупповых
|
факторная дисперсия
|
Эмпирическое
корреляционное отношение
|
|
3219,1155556
|
595,5822222
|
2623,5333333
|
0,9027656
|
Таблица 2.5
Линейный коэффициент корреляции признаков
|
|
Столбец 1
|
Столбец 2
|
|
Столбец
1
|
1
|
|
|
Столбец
2
|
0,91318826
|
1
|
Вывод итогов
|
Регрессионная статистика
|
|
Множественный R
|
0,91318826
|
|
R-квадрат
|
0,833912798
|
|
Нормированный R-квадрат
|
0,827981112
|
|
Стандартная ошибка
|
23,93414838
|
|
Наблюдения
|
30
|
Дисперсионный анализ
|
Нижние
95%
|
Верхние
95%
|
Нижние
68,3%
|
Верхние
68,3%
|
|
-84,85505829
|
18,33659391
|
-58,92212786
|
-7,596336521
|
|
0,901157173
|
1,277553188
|
0,995748659
|
1,182961703
|
|
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
|
Y-пересечение
|
-33,25923219
|
25,18823876
|
-1,320427066
|
0,197384751
|
|
Переменная X 1
|
1,089355181
|
0,09187519
|
11,85690257
|
1,97601E-12
|
|
|
df
|
SS
|
MS
|
F
|
Значимость
F
|
|
Регрессия
|
1
|
80533,84982
|
80533,84982
|
140,586138
|
1,97601E-12
|
|
Остаток
|
28
|
16039,61685
|
572,8434589
|
|
|
|
Итого
|
29
|
96573,46667
|
|
|
|
Вывод остатка
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
|
1
|
151,9311486
|
-11,93114857
|
|
2
|
167,1821211
|
18,8178789
|
|
3
|
184,611804
|
-24,611804
|
|
4
|
191,1479351
|
14,85206491
|
|
5
|
199,8627765
|
20,13722347
|
|
6
|
204,2201973
|
27,77980274
|
|
7
|
221,6498802
|
-23,64988015
|
|
8
|
228,1860112
|
-38,18601124
|
|
9
|
232,543432
|
-6,543431962
|
|
10
|
241,2582734
|
10,74172659
|
|
11
|
243,4369838
|
24,56301623
|
|
12
|
249,9731149
|
-3,973114857
|
|
13
|
254,3305356
|
3,669464419
|
|
14
|
256,5092459
|
23,49075406
|
|
15
|
263,045377
|
-13,04537703
|
|
16
|
265,2240874
|
-9,22408739
|
|
17
|
271,7602185
|
-31,76021848
|
|
18
|
271,7602185
|
20,23978152
|
|
19
|
271,7602185
|
-11,76021848
|
|
20
|
280,4750599
|
43,52494008
|
|
21
|
293,5473221
|
-33,5473221
|
|
22
|
297,9047428
|
6,095257181
|
|
23
|
300,0834532
|
21,91654682
|
|
24
|
302,2621635
|
-42,26216354
|
|
25
|
308,7982946
|
-10,79829463
|
|
26
|
310,977005
|
-36,97700499
|
|
27
|
317,5131361
|
36,48686392
|
|
28
|
332,7641086
|
7,235891391
|
|
29
|
341,4789501
|
8,521049943
|
|
30
|
369,8021848
|
10,19781524
|
Рисунок 2.1
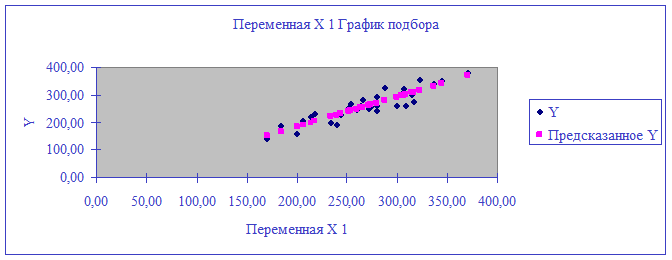
Рисунок 2.2
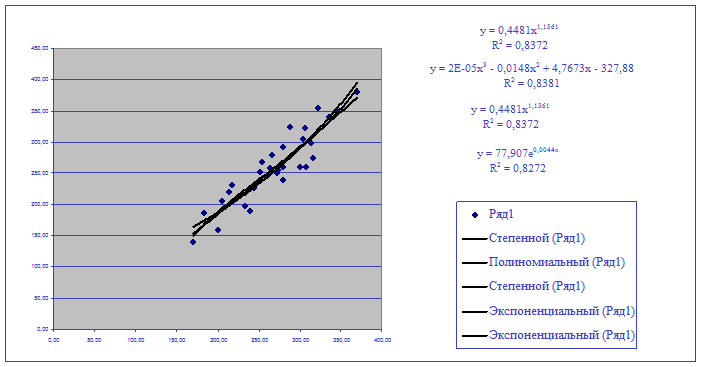
Рисунок 2.3
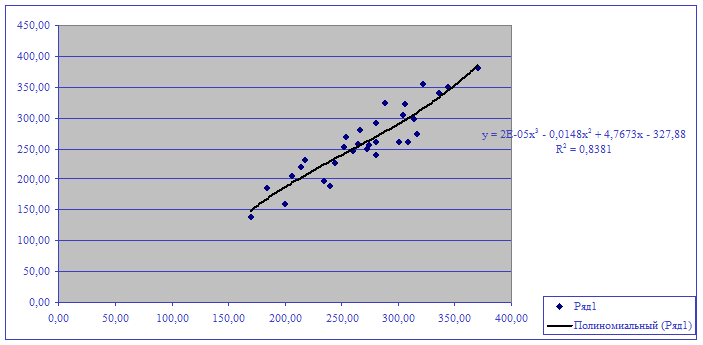
III.
Выводы по результатам выполнения лабораторной работы.
Задание 1. Построение аналитической группировки зависимости
результативного признака от факторного и оценка тесноты корреляционной связи
признаков.
Аналитическая
группировка зависимости признака Выпуск
продукции от признака Среднегодовая стоимость
основных фондов представлена в таблице 2.2. рабочего файла.
Т.к.
эмпирическое корреляционное отношение η = 0,903, то можно сделать вывод о
наличие тесной корреляционной связи. r = 0,913. r> η. Следовательно, можно сделать вывод о
возможности линейной связи между признаками.
Задание 2. Построение однофакторной линейной регрессионной
модели связи изучаемых признаков с помощью инструмента Регрессия надстройки Пакет
анализа.
Уравнение
однофакторной линейной регрессионной модели связи выглядит следующим образом: 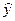 =a
=a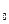 +a
+a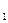 x.
x.
Однофакторную
линейную регрессионную модель связи изучаемых признаков построим с помощью
программы Регрессия надстройки Пакет анализа.
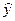 =1,0894x-33,26
=1,0894x-33,26
Задание 3. Построение аналитических моделей связи признаков
для линейной и нелинейных форм связи с помощью инструмента Мастер диаграмм и выбор наиболее адекватного уравнения регрессии.
С помощью
инструмента Мастер диаграмм построим аналитические модели связи признаков для
линейной и нелинейных форм связи.
Т. к.
коэффициент детерминации R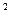 больше в полиномиальном уравнении 3-го порядка, то именно эта модель признается
наиболее адекватной.
больше в полиномиальном уравнении 3-го порядка, то именно эта модель признается
наиболее адекватной.
Построенные регрессионные модели связи
|
Вид
уравнения
|
Уравнение
регрессии
|
Коэффициент
детерминации
R2
|
|
Линейное
|
Y=
1,0894x-33,26
|
0,8339
|
|
Полином 2-го порядка
|
Y=
0,0008x²+0,6846x+18,955
|
0,8353
|
|
Полином 3-го порядка
|
Y=
2E-05x³-0,0148x²+4,7673x-327,88
|
0,8381
|
|
Степенное
|
1,1381
Y=0,4481x
|
0,8372
|
|
Экспоненциальное
|
0,0044х
Y=77,907e
|
0,8272
|