Задача 6

Определить силу давления на коническую крышку горизонтального цилиндрического сосуда диаметром D1=1500 мм, заполненного керосином. Показания манометра в точке его присоединения – рм=0,4 МПА (абс). Показать на чертеже вертикальную и горизонтальную составляющие, а также полную силу давления. При этом а=900 мм.

Решение:

Для наглядности проиллюстрируем решение задачи графически.

Пусть жидкость заполняет резервуар, правая стенка которого представляет собой цилиндрическую криволинейную поверхность АВС (рис.1), простирающуюся в направлении читателя на ширину b. Восстановим из точки А перпендикуляр АО к свободной поверхности жидкости. Объем жидкости в отсеке АОСВ находится в равновесии. Это значит, что силы, действующие на поверхности выделенного объема V, и силы веса взаимно уравновешиваются.

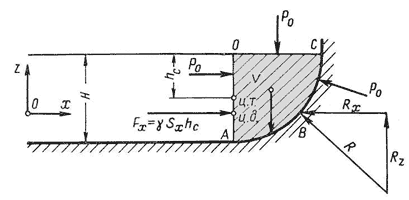
Рис. 1. Схема гидростатического давления на цилиндрическую поверхность

На рисунке показаны составляющие силы реакции стенки, которые равны по модулю, но противоположны по направлению соответствующим компонентам силы давления

Cила гидростатического давления на площадь Sx по направлению оси Ох равна Fx = γ Sx hc , где hc – высота центра давления, который находится по формуле

.

Площадь боковой поверхности конуса .

Плотность керосина γ = 8000 Н/м3.

Тогда

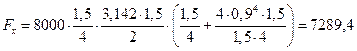Н.

Аналогично находятся остальные две составляющие этой силы – по осям Oy и Oz.

Тогда полная сила давления:

= Н.

Задача 18

При внезапном расширении трубопровода скорость жидкости в трубе большего диаметра равна  v=2,5 м/с. Отношение диаметров труб D:d=2. Определить h – разность показаний пьезометров.

Решение:

Найдем разность давлений (Р – р) в двух разных участках трубы, затем разность показаний пьезометров найдем как  h = (Р – р) / γ.

В свою очередь разность давлений найдем из уравнения неразрывности, т.е. из условия одинакового расхода жидкости на обеих участках:

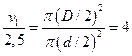;   ;  откуда скорость на маленьком участке трубы 10 м/с.

По закону Бернулли , откуда Р = 4 ∙ р. Тогда искомая разность показаний

h = (Р – р) / γ = 3р/γ,

где величины  р и  γ зависят от незаданных в условии задачи параметров жидкости.

Задача 21

Определить время закрытия задвижки, установленной на свободном конце стального водопровода диаметром d=150 мм, длиной l = 1700 м, с толщиной стенки d=8 мм, при условии, чтобы максимальное повышение давления в водопроводе было в три раза меньше, чем при мгновенном закрытии задвижки. Через сколько времени после мгновенного закрытия задвижки повышение давления распространится до сечения, находящегося на расстоянии 0,7l от задвижки?

Решение:

Скачок давления распространяется по трубе в виде упругой волны со скоростью u, определяемой коэффициентом сжимаемости и плотностью жидкости, модулем упругости материала трубы, ее диаметром и толщиной стенок. Для потоков воды в стальных и чугунных трубах  u ” 1000 – 1350 м/с.

Если жидкость плотности  ?  течет со скоростью  v  в трубопроводе с площадью сечения  S  , а задвижка в конце трубопровода закрывается за время (?t)з, то возникает увеличение давления  ?p  . В прилегающем к задвижке слое жидкости длиной  ?l= u(?t)з и массой  m=?S?l, теряется импульс ?(mv)=?S?lv. По второму закону Ньютона изменение импульса определяется величиной действующей силы: ?(mv)/ (?t)з = F. Учитывая, что  F =?pS , получаем выражение для величины скачка давления:

                                               ?p = ?vu    

Образующееся при гидравлическом ударе повышение давления распространяется против течения жидкости и  через время  L/u  ( L-длина трубопровода) достигает резервуара. Здесь давление падает, и это падение давления передается обратно к задвижке с той же скоростью в виде отраженной волны (волна понижения). Циклы повышений и понижений давления чередуются через промежутки времени  3L/u при условии троекратного скачка давления, пока этот колебательный процесс не затухнет из-за потерь энергии на трение и деформацию стенок. Эта формула   действительна лишь в случае, когда время закрытия запорного устройства сравнительно мало, т.е. при условии (?t)з < 3L/u. При (?t)з > 3L/u отраженная волна придет к запорному устройству раньше, чем задвижка закроется, и повышение давления в трубопроводе уменьшится. Из этого условия и найдем время, точнее установим, что время должно быть меньше следующей величины:

(?t)з < 3L/u.

(?t)з < 3 ∙ 0,7 ∙ 1,7 м / 1000 (м/с).

Отсюда искомый интервал времени

(?t)з <0,00357 с.

Задача 25

Определить производительность и напор насоса (рабочую точку) при подаче воды в открытый резервуар из колодца на геодезическую высоту Нг = 6 м по трубопроводу диаметром  d = 250 мм, длиной  l = 40 м, с коэффициентом гидравлического трения  и эквивалентной длинной местных сопротивлений  le = 8 м. Как изменится подача и напор насоса, если частота вращения рабочего колеса уменьшится на 10%?

Решение:

Для развития максимальной производительности насоса на уровне м3/с при необходимости подачи воды в открытый резервуар из колодца на геодезическую высоту Нг = 6 м по трубопроводу диаметром  d = 250 мм, длиной  l = 40 м, с коэффициентом гидравлического трения  и эквивалентной длиной местных сопротивлений  lэкв = 8 м максимальный напор насоса найдется из соотношения:

.

Выразим из этого соотношения максимальный напор и подставим численные значения:

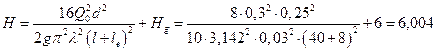 м.

При расчете подачи и напора насоса при изменении частоты вращения рабочего колеса на 10% следует иметь в виду, что в таблице с исходными данными показана производительность насоса с шагом 20%. Для ответа на поставленный вопрос составим таблицу с шагом 10%, исходя их предположения о линейной связи  Q – H  на каждом 20%-ом отрезке; тогда соответствующие коэффициенты в точках 0,1, 0,3, 0,5, 0,7, 0,9 найдутся как средние арифметические соседних коэффициентов при  Н:

0

0.1

0.2

0.3

0,4

0,5

0,6

0,7

0,8

0,9

H

1,025

1,05

1,025

1,44

1,88

1,265

0,65

0,5

0,35

Так, при снижении производительности с максимальной до 90% напор увеличится и составит:

 м.

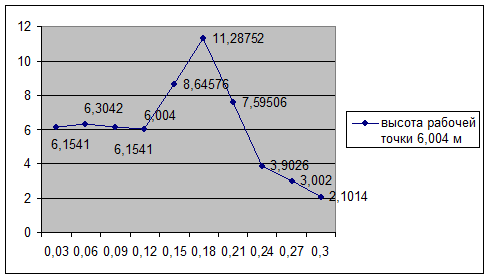
Для построения характеристики "насос – сеть" задаемся рядом значений расхода, вычисляем полные напоры, соответствующие этим расходам. При заданных значениях Q вычисляются значения Н. После чего, на одном графике, в одном масштабе выполняются построения характеристики Q-Н насоса и характеристик трубопроводов, далее графически определяется (пересечением кривых) рабочий режим насоса.

Q

0,03

0,06

0,09

0,12

0,15

0,18

0,21

0,24

0,27

0,3

H

6,1541

6,3042

6,1541

6,004

8,64576

11,28752

7,59506

3,9026

3,002

2,1014

По горизонтальной оси откладываются значения расхода воды. Пересечение графика Q-Н с горизонтальной линией, показывающей рабочую точку насоса, показывает рабочий режим насоса – приблизительно Q = 0,22 м3/с.

Задача 30

Поршневой насос простого действия с диаметром цилиндра D=90 мм, ходом поршня S=260 мм, числом двойных ходов в минуту п=75 ход/мин и объемным КПД hоб=0,9 подает рабочую жидкость в систему гидропровода. При какой частоте вращения должен работать включенный параллельно шестеренный насос с начальным диаметром шестерен d=72 мм, шириной шестерен b=65 мм, числом зубьев z=30 и объемным КПД  hоб=0,86, чтобы количество подаваемой жидкости удвоилось?

Решение:

Поршневой насос простого действия с диаметром цилиндра D=90 мм, ходом поршня S=260 мм, числом двойных ходов в минуту п=75 ход/мин и объемным КПД hоб=0,9 подает рабочую жидкость в количестве

 м3/мин.

Для расчета минутной подачи насосов с двумя одинаковыми шестернями можно пользоваться формулой

Q = η0A(Dг- A)bN ,

где η0 - объемный КПД насоса, зависящий от конструкции, технологии изготовления и давления насоса и принимаемый равным 0,7-0,95; А - расстояние между центрами шестерен, равное диаметру начальной окружности D; Dг - диаметр окружности головок зубьев; b - ширина шестерен; N - частота вращения ротора, об/мин.

Согласно условию задачи, количество подаваемой жидкости должно удвоиться, тогда искомая частота вращения:

N = η0A(Dг-A)b / (2∙Q) = 0,9∙30∙(72-30)∙65 / (2∙0,002) = 302 об/мин.

Задача 41

Пользуясь характеристикой, приведенной в задаче 40, определить активный диаметр и построить внешнюю (моментальную) характеристику гидромуфты, предназначенной для работы с асинхронным электродвигателем, развивающим максимальный крутящий момент М=350 Н×м при частоте вращения п=1100 об/мин. Рабочая жидкость – минеральное масло.

Указание: Активный диаметр может быть определен по уравнению моментов совмещением режимов гидромуфты при  l=0 и электродвигателя при максимальном моменте М.

Решение:

В гидромуфте (гидропередача без внешней опоры) момент на турбине всегда равен моменту на насосе, но передача энергии в ней происходит с определенными потерями, характеризуемыми в рабочем режиме  значением  К.П.Д. Поскольку моменты колес раны, то  К.П.Д. численно равен отношению частоты вращения турбины n2 к частоте вращения насоса n1, т.е. передаточному отношению  i ( i= n2/n1).

Момент гидромуфты Мг  подчиняется зависимости

М = λi·ρ·(n / 60)2·Da,       где:

λi - коэффициент момента, являющийся параметром гидромуфты данного типа при заданном значении i, ρ-плотность РЖ, Da- активный диаметр, равный наибольшему диаметру рабочей полости гидромуфты. 

Отсюда искомый активный диаметр:

Da = М / (λi·ρ·(n / 60)2) = 350 / (60∙10-7 ∙ 8600 ∙ (1100 / 60)2) = 0,202 м.

Построим внешнюю (моментальную) характеристику гидравлической муфты. В эту характеристику входят:

1)    момент муфты: М = 350 Н∙м;

2)    коэффициент момента λi = 60∙10-7 мин2/м;

3)    активный диаметр: Da = 0,202 м;

4)    частота вращения  п = 1100 об/мин.