Контрольная работа

1. Решить уравнение или неравенство:

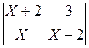 = 2

(X + 2)×(X – 2) – 3X = 2

X² – 4 – 3X – 2 = 0,

X² – 3X – 6 = 0,

D = 9 + 24 = 33,             =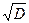

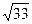
X₁ = 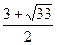,                  X₂ =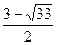

Ответ:         .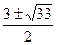

2. Найти матрицу X, если заданы матрицы A, B, C и вычислить её определитель

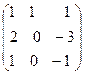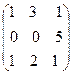A = ;             B = ;                C =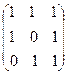

Найти X = (7B^-1 + B)×CA + BE,

          и 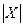 = detX.

Найдём B^-1:

B^-1 =  .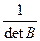

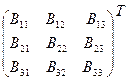DetB =  = – 5×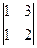 = – 5×(2 – 3) = 5;

B₁₁ = 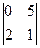 = – 10;                   B₁₂ = –  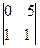= 5;           B₁₃ =  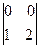= 0;

B₂₁ = – 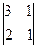 = – 1;         B₂₂ =  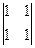= 0;               B₂₃ = –  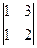= 1;

B₃₁ = 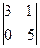 = 15;            B₃₂ = –  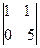= – 5;                  B₃₃ =  = 0.

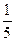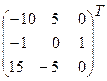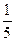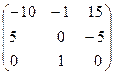B^-1 = × = × =  Þ

Þ 7B^-1 + B =  +  = ;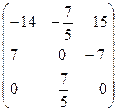

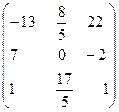C×A = × =  = ;

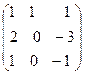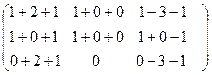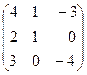(7B^-1 + B)×C×A = × = ;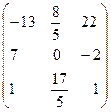

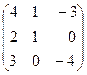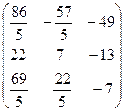Þ X = (7B^-1 + B)×C×A +  =  +  =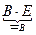

= .

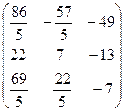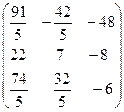DetX = 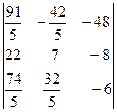  суммируем 1 и 3 строку =  =

= × = × =

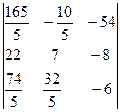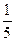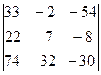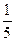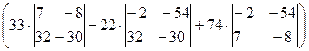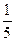= ×(1518 – 39336 + 29156) = – 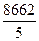 = – 1732,4.

Ответ:         X = 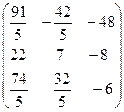,      DetX = – 1732,4.

3. Решить систему уравнений методом Крамера и Гаусса:

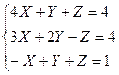
а) Метод Крамера:

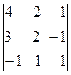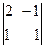D =  = 4× – 3×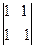 + (–1)× =

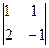= 4×(2 + 1) – 3×(1 – 1) – (– 1 – 2) = 12 + 3 = 15;

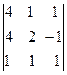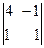D_X =  = 4× – 4× +  =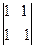

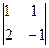= 4×3 – 4×0 + (–3) = 12 – 3 = 9;

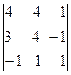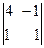D_Y =  = 4× – 3×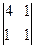 + (–1)× =

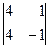= 4×(4 + 1) – 3×(4 – 1) – (– 4 – 4) = 4×5 – 3×3 + 8 = 20 – 9 + 8 = 19;

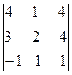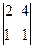D_Z =  = 4× – 3×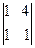 + (–1)× =

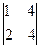= 4×(2 – 4) – 3×(1 – 4) – (4 – 8) = – 8 + 9 + 4 = 5;

Þ X =  =  =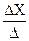

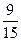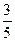
Y =  =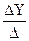

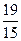
Z =  =  =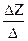

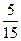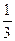
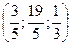
б). Метод Гаусса:

            

         

       

        

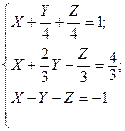
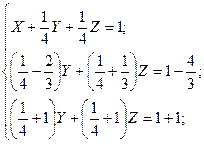
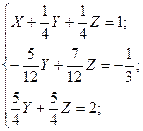
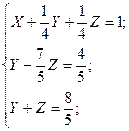
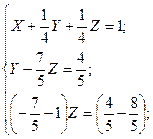
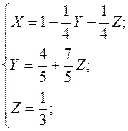
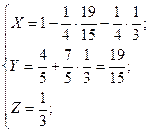
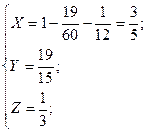
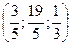
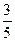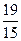Ответ:         X = ;        Y = ;       Z = .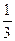

4. Найти фундаментальную систему решений и общее решение систем: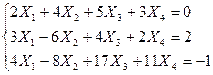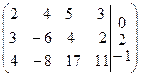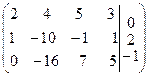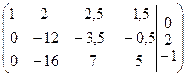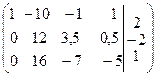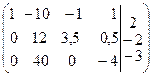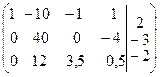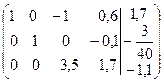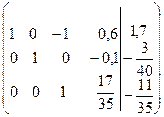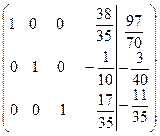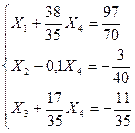

 ~  ~  ~

 ~  ~  ~

 ~  ~

Þ  Þ .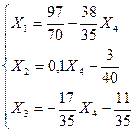

Ответ: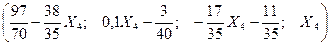        

5. Найти пределы функций:

а).  =  =  =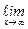

=

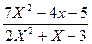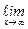
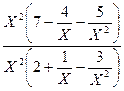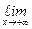
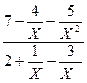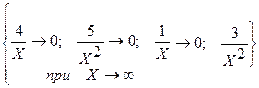
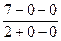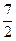=  =  = 3,5.

б).  =  =  =  =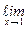

=  =  =

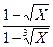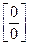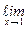
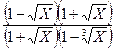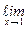
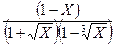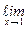
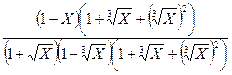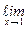
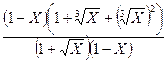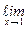
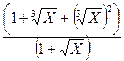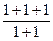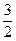=  =  =  = 1,5.

в).  =  =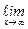

=  =

 =

=  =

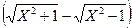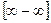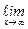
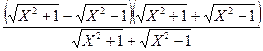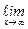
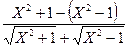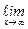
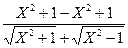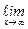
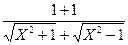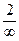=  =  = 0.

Ответ:         а) 3,5

                   б) 1,5

                   в) 0

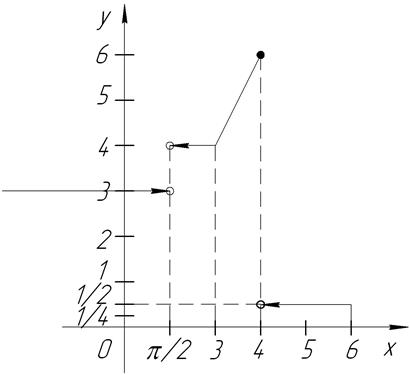
6. Исследовать на непрерывность данные функции и классифицировать точки разрыва, если такие найдутся:

Y =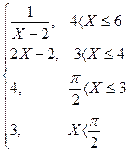

Y₁ = 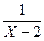 непрерывна в точках X ¹ 2, но 2 Ï (4; 6], поэтому Y₁ =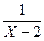

непрерывна на (4; 6].

Y₂ = 2X – 2;                  Y₃ = 4;        Y₄ = 3 – непрерывны на всей числовой оси.

Поэтому подозрительными на разрыв будут точки: X₁ = 4;        X₂ = 3;   X₃ = .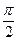

Исследуем их, используя критерий непрерывности.

X₁ = 4

Y(4) = 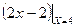 = 8 –2 = 6,

Функция определёна в точке X₁.

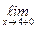Y(x) = 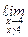Y(x) =  =  = ;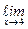

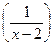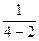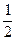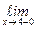 Y(x) = 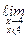Y(x) = 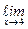(2x – 2) = 2×4 – 2 = 6;

Þ предел справа не равен пределу слева ,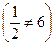

но они конечны, поэтому X₁ = 4 – точка разрыва I рода.

X₂ = 3

Y(3) = 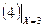 = 4, функция определена

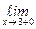 Y(x) = 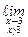Y(x) = 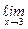(2x – 2) = 2×3 – 2 =4,

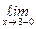 Y(x) = 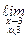Y(x) = 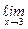4 = 4

Þ предел справа равен пределу слева и они равны значению функцию в этой точке Þ функция непрерывна в точке X₂.

X₃ = .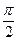

Y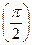 не определена.

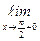 Y(x) = 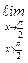Y(x) = 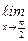(4) = 4;

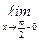 Y(x) = 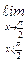Y(x) = 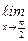(3) = 3.

Þ предел справа не равен слева, но они конечны, Þ X₃ – точка разрыва I рода.

Ответ: функция непрерывна на [6; + ¥) за исключением точек X = 4 и X = 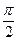.