Содержание
Задание 1. Составить линейную оптимизационную модель и решить ее при помощи надстройки «Поиск решения» в Excel............................................................................................................. 3
Задание 2. Сетевое и календарное планирование..................................................................... 6
Задача 3. Управление запасами................................................................................................. 12
Задание 1. Составить линейную оптимизационную модель и решить ее при помощи надстройки «Поиск решения» в Excel.
Фирма выпускает три вида продукции (изделий). В процессе производства используются три технологические операции. На рис. 1 показана технологическая схема производства изделий видов 1, 2 и 3. При изготовлении изделия 2 технологическая операция 2 не выполняется, а при производстве изделия 3 используются только технологические операции 1 и 2. В прямоугольниках на рис. 1 указана длительность технологических операций при изготовлении изделия каждого вида.
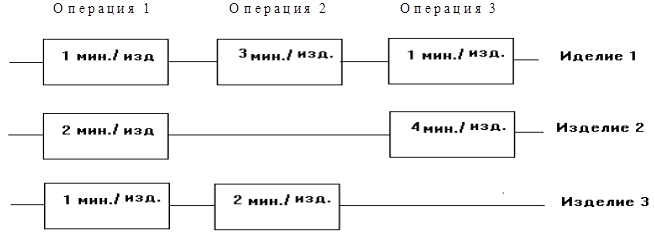
Рис. 1. Технологическая схема производства изделий
Так как эти технологические операции используются фирмой и для других производственных целей, фонд рабочего времени, в течение которого операции 1, 2 и 3 могут быть применены для производства рассматриваемых изделий, ограничен следующими предельными значениями (в сутки):
для первой операции - 430 мин,
для второй операции - 460 мин,
для третьей операции - 420 мин.
Изучение рынка сбыта показало, что ожидаемая прибыль от продажи одного изделия видов 1, 2 и 3 составляет 3,2 и 5 руб. соответственно.
Каков наиболее выгодный суточный объем производства каждого вида изделия?
Как уже было показано, построение математической модели следует начинать с идентификации управляемых переменных (искомых величин). После этого определяются целевая функция и ограничения через соответствующие переменные.
Пусть
X1 - количество производимых изделий вида 1,
X2 - количество производимых изделий вида 2,
X3 - количество производимых изделий вида 3.
При использовании этих обозначений математическая формулировка задачи принимает вид
F(![]() )= 3×X1 + 2×X2 + 5×X3
)= 3×X1 + 2×X2 + 5×X3 ![]() (целевая функция)
(величина прибыли за сутки)
(целевая функция)
(величина прибыли за сутки)
при ограничениях
для операции 1: 1×X1 + 2×X2 + 1×X3 £ 430 (предельное время
для операции 2: 3×X1 + 0×X2 + 2×X3 £ 460 использования операций
для операции 3: 1×X1 + 4×X2 + 0×X3 £ 420 в течение суток)
X1, X2, X3 ³ 0.
Задачи производственного менеджмента во многих случаях оказываются ассоциированными с задачами распределительного типа, т.е. с задачами, в которых требуется распределить ограниченные ресурсы по нескольким видам производственной деятельности.
Рассмотрим следующую ситуацию, получившую название задачи производственного планирования. Пусть из технологических соображений известен перечень продуктов, которые предприятие может производить без дополнительных капиталовложений. Кроме того, известны вид и количество ресурсов отпущенных предприятию для производственного потребления и структура материальных затрат и доходов. В этих условиях перед предприятием стоит задача выбора плана производства, обеспечивающего получение максимальной прибыли.
Перейдем
к построению математической модели рассмотренной ситуации. Будем
считать, что предприятие может
производить n различных
продуктов (j = 1, ..., n). Количество j-го
продукта выпускаемого по
плану, обозначим через xj. В этом случае план производства может быть
описан с помощью вектора ![]() = (X1, X2, ..., Xn).
Предположим, что предприятие
располагает для организации производственного
процесса m видами различных ресурсов (i = 1, ...,
m). Количество ресурса
i-го вида, отпущенное предприятию
для потребления обозначим через bi.
Количество ресурса i-го вида, расходуемое предприятием на производство единицы j-го
продукта, обозначим через aij,
а прибыль, от
производства единицы продукции
j-го вида через cj.
= (X1, X2, ..., Xn).
Предположим, что предприятие
располагает для организации производственного
процесса m видами различных ресурсов (i = 1, ...,
m). Количество ресурса
i-го вида, отпущенное предприятию
для потребления обозначим через bi.
Количество ресурса i-го вида, расходуемое предприятием на производство единицы j-го
продукта, обозначим через aij,
а прибыль, от
производства единицы продукции
j-го вида через cj.
Тогда, в принятых нами обозначениях, задача выбора плана производства, обеспечивающего получение максимальной прибыли может быть сформулирована как математическая задача в следующем виде:
Найти вектор-план ![]() =(X1,X2,...,Xn),
удовлетворяющий системе ограничений
=(X1,X2,...,Xn),
удовлетворяющий системе ограничений
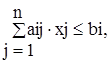 i=1,...,m,
i=1,...,m,
Xj![]() 0 ,
0 , ![]()
и доставляющий целевой функции задачи
F(![]() ) =
) = 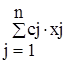
максимальное значение.
 Рис. 1. Геометрическая интерпретация задачи производственного
планирования
Рис. 1. Геометрическая интерпретация задачи производственного
планирования
Задание 2. Сетевое и календарное планирование
Построение календарного графика, расчет и представление на графике временных характеристик событий, расчет временных характеристик работ. Оптимизация модели по критериям:
а) минимум исполнителей при условии неизменности сроков выполнения работ;
б) минимум срока выполнения проекта (исходя из того, что любая работа может быть изменена по сроку исполнения и ресурсам в 2 раза);
в) минимум исполнителей при условии неизменности срока выполнения проекта и при том, что работы, не входящие в критический путь, могут быть изменены по времени выполнения и по ресурсам в 2 раза.
Таблица 3
|
Название работы |
Нормальная длительность |
Количество исполнителей |
Вариант 6 (N = 10 человек) 1. F, C. B – исходные работы проекта, которые можно начинать одновременно; 2. Работа Е следует за F 3. Работа А следует за В, а работа G – за А; 4. Работа D и J следует за E; 5. Работы I следуют за C, но не могут начаться, пока не завершена J и G; 6. Работа Н следует за D. |
|
A |
9 |
1 |
|
|
B |
3 |
1 |
|
|
C |
12 |
7 |
|
|
D |
6 |
1 |
|
|
E |
8 |
2 |
|
|
F |
4 |
10 |
|
|
G |
7 |
3 |
|
|
H |
10 |
4 |
|
|
I |
7 |
2 |
|
|
J |
12 |
1 |
Решение
Составим по данным табл. 3 структурную таблицу с указанием для каждой работы непосредственно предшествующих ей работ (опорных работ).
Таблица 4
|
Название работы |
Непосредственно предшествующие работы |
Предшествующие работы |
|
A |
- |
- |
|
B |
F |
|
|
C |
B, I, J |
|
|
D |
E, C |
|
|
E |
H |
|
|
F |
- |
- |
|
G |
- |
- |
|
H |
F |
|
|
I |
G |
|
|
J |
A |
|
|
K |
B, I, J |
По данным табл. 4 построим сетевой график в виде стрелочного графа (см. рис. 3). Каждая вершина графа означает событие, а дуга – работу.
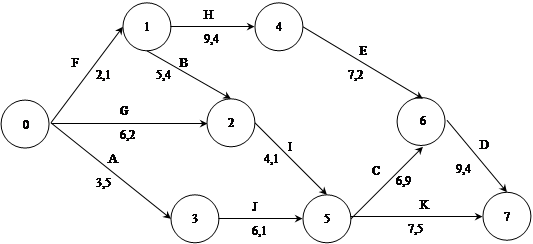 |
Рис. 3.
Определим временные характеристики событий и работ.
Начнем с временных характеристик событий. Ранний (или ожидаемый) срок tp(i) свершения i-го события определяется продолжительностью максимального пути, предшествующего этому событию:
![]() ,
(1)
,
(1)
где L1i – любой путь, предшествующий i-му событию.
Если событие j имеет несколько предшествующих путей (событий i), то ранний срок свершения события j равен
![]() .
(2)
.
(2)
Поздний (или предельный) срок tn(i) свершения i-го события равен:
![]() ,
(3)
,
(3)
где L2i – любой путь, следующий за i-м событием,
tkp – продолжительность критического пути.
Если событие i имеет несколько последующих путей (событий j), то ранний срок свершения события j равен
![]() .
(4)
.
(4)
Резерв времени R(i) i-го события равен:
![]() .
(5)
.
(5)
Определим по формулам (1) – (5) значения временных характеристик событий.
Для анализируемого графа критический путь включает следующие работы: F, H, E, D. Он равен
tkp = 2 + 9 + 7 + 9 = 27.
Для i = 0 (нулевого события) очевидно, что tp(0) = 0.
Для i = 1 tp(1) = 0 + 2 = 2.
Для i = 2 tp(2) = max{0 + 6; 2 +5} = 7.
Для i = 3 tp(3) = 0 + 3 = 3.
Для i = 4 tp(4) = 2 + 9 = 11.
Для i = 5 tp(5) = max{7 + 4; 3 + 6} = 11.
Для i = 6 tp(6) = max{11 + 7; 11 + 6} = 18.
Для i = 7 tp(7) = tkp = 18 + 9 = 27.
Т.к. i = 7 - завершающее событие, то tn(7) = tp(7) = 27.
Для i = 6 tn(6) = 27 - 9 = 18.
Для i = 5 tn(5) = min{18 - 6; 27 - 7} = 14.
Для i = 4 tn(4) = 18 - 7 = 11.
Для i = 3 tn(3) = 14 - 6 = 8.
Для i = 2 tn(2) = 14 - 4 = 10.
Для i = 1 tn(1) = 11 - 9 = 2.
Для i = 0 tn(0) = min {2 - 2; 10 - 6; 8 - 3} = 0.
Резервы времени событий равны:
Для i = 0 R(0) = 0.
Для i = 1 R(1) = 2 - 2 = 0.
Для i = 2 R(2) = 8 - 7 = 1.
Для i = 3 R(3) = 8 - 3 = 5.
Для i = 4 R(4) = 11 - 11 = 0.
Для i = 5 R(5) = 14 - 11 = 3.
Для i = 6 R(6) = 18 - 18 = 0.
Для i = 7 R(7) = 27 - 27 = 0.
Определим далее временные характеристики работ.
Ранний срок tpn(i,j) начала работы (i,j) определяется по формуле:
![]() .
(6)
.
(6)
Ранний срок tpo(i,j) окончания работы (i,j) определяется по формуле:
![]() .
(7)
.
(7)
Поздний срок tpn(i,j) окончания работы (i,j) определяется по формуле:
![]() .
(8)
.
(8)
Поздний срок tnn(i,j) начала работы (i,j) определяется по формуле:
![]() .
(9)
.
(9)
Определим по формулам (6) - (9) временные характеристики всех работ.
Для работы A:
tpn = 0; tpo = 3; tnn = 5; tno = 8.
Для работы B:
tpn = 2; tpo = 7; tnn = 5; tno = 10.
Для работы C:
tpn = 11; tpo = 17; tnn = 12; tno = 18.
Для работы D:
tpn = 18; tpo = 27; tnn = 18; tno = 27.
Для работы E:
tpn = 11; tpo = 18; tnn = 11; tno = 18.
Для работы F:
tpn = 0; tpo = 2; tnn = 0; tno = 2.
Для работы G:
tpn = 0; tpo = 6; tnn = 4; tno = 10.
Для работы H:
tpn = 2; tpo = 11; tnn = 2; tno = 11.
Для работы I:
tpn = 7; tpo = 11; tnn = 10; tno = 14.
Для работы J:
tpn = 3; tpo = 9; tnn = 8; tno = 14.
Для работы K:
tpn = 11; tpo = 18; tnn = 20; tno = 27.
Оптимизируем сетевой график по критерию минимума исполнителей. Находим суммарное количество исполнителей для всех полных путей сетевого графика. Полных путей в графике всего семь:
- первый (0,1,4,6,7);
- второй (0,1,2,5,6,7);
- третий (0,1,2,5,7);
- четвертый (0,2,5,6,7);
- пятый (0,2,5,7);
- шестой (0,3,5,6,7);
- седьмой (0,3,5,7).
Первый путь (0,1,4,6,7) требует выполнения работ F, H, E, D. При этом потребуется 1 + 4 + 2 + 4 = 11 исполнителей.
Второй путь (0,1,2,5,6,7) требует выполнения работ F, B, I, C, D. При этом потребуется 1 + 4 + 1 + 9 + 4 = 19 исполнителей.
Третий путь (0,1,2,5,7) требует выполнения работ F, B, I, K. При этом потребуется 1 + 4 + 1 + 5 = 11 исполнителей.
Четвертый путь (0,2,5,6,7) требует выполнения работ G, I, C, D. При этом потребуется 2 + 1 + 9 + 4 = 16 исполнителей.
Пятый путь (0,2,5,7) требует выполнения работ G, I, K. При этом потребуется 2 + 1 + 5 = 8 исполнителей.
Шестой путь (0,3,5,6,7) требует выполнения работ A, J, C, D. При этом потребуется 5 + 1 + 9 + 4 = 19 исполнителей.
Седьмой путь (0,3,5,7) требует выполнения работ A, J, K. При этом потребуется 5 + 1 + 5 = 11 исполнителей.
Оптимальной моделью по критерию минимума исполнителей является выполнение работ G, I, K.
Оптимизируем сетевой график по критерию минимума сроков выполнения. Находим суммарные сроки выполнения комплекса работ для всех полных путей сетевого графика.
Первый путь потребует 2 + 9 + 7 + 9 = 27 дней.
Второй путь потребует 2 + 5 + 4 + 6 + 9 = 26 дней.
Третий путь потребует 2 + 5 + 4 + 7 = 18 дней.
Четвертый путь потребует 6 + 4 + 6 + 9 = 25 дней.
Пятый путь потребует 6 + 4 + 7 = 17 дней.
Шестой путь потребует 3 + 6 + 6 + 9 = 24 дней.
Седьмой путь потребует 3 + 6 + 7 = 16 дней.
Т.к. по условию любая работа и ресурсы могут быть изменены в два раза, то каждый из возможных комплексов работ может уменьшиться по времени в четыре раза (сокращение в два раза длительностей работ и увеличение ресурсов в два раза). Полученные длительности при этом для всех семи возможных комплексов работ сохраняют свои пропорции. Следовательно, оптимальной моделью по критерию минимума сроков выполнения является седьмой путь, т.е. выполнение работ A, J, K.
Оптимизируем сетевой график по критерию минимума исполнителей при условии что работы, не входящие в критический путь, могут быть изменены по времени выполнения и по ресурсам в 2 раза. Каждая работа, не входящая в критический путь, по числу исполнителей может быть уменьшена в четыре раза.
Первый путь потребует 1 + 4 + 2 + 4 = 11 исполнителей.
Второй путь потребует 1 + 4/4 + 1/4 + 9/4 + 4 = 34/4 = 8,5 исполнителей.
Третий путь потребует 1 + 4/4 + 1 + 5 = 8 исполнителей.
Четвертый путь потребует 2/4 + 1/4 + 9/4 + 4 = 7 исполнителей.
Пятый путь потребует 2/4 + 1/4 + 5/4 = 8/4 = 2 исполнителей.
Шестой путь потребует 5/4 + 1/4 + 9/4 + 4 = 7,75 исполнителей.
Седьмой путь потребует 5/4 + 1/4 + 5/4 = 11/4 = 3,75 исполнителей.
Оптимальной моделью по критерию минимума исполнителей при условии что работы, не входящие в критический путь, могут быть изменены по времени выполнения и по ресурсам в 2 раза является пятый путь, т.е. выполнение работ G, I, K.
Задача 3. Управление запасами
Завод радиоэлектронной аппаратуры производит x1 = 580 радиоприемников в сутки. Микросхемы для радиоприемников (по 1 шт. на приемник) производятся на этом же заводе с интенсивностью х2 = 2600 шт. в сутки. Затраты на подготовку производства партии микросхем составляют х3 = 29 руб. (числа в задаче условные), себестоимость производства 1 тыс. шт. микросхем равна х4 = 7,4 руб. Хранение микросхем на складе обходится заводу в х5 = 1,4 руб., за каждую тысячу в сутки. У завода появилась возможность закупать микросхемы в другом месте по цене х6 = 6.5 руб. за 1 тыс. шт. Стоимость доставки равна х7 = 16 руб.
Выясните, стоит ли заводу закупать микросхемы вместо того, чтобы их производить. Для более выгодного режима работы завода (производство или закупка) определите периодичность подачи заказа, и затраты на управление запасами в месяц (22 рабочих дня).
Решение
Определим оптимальный объем производства и периодичность подачи заказа на микросхемы для обоих случаев.
1. Выпуск микросхем на заводе.
Уравнение издержек за год имеет вид:
C = C1 + C2 + C3,
где C1 - общие организационные издержки; C2 - стоимость микросхем; C3 - общие издержки содержания (хранения) запасов.
Общие организационные издержки равны
![]() руб,
руб,
где q – количество микросхем в одной партии (тыс. шт.).
Стоимость микросхем равна
![]() руб.
руб.
Общие издержки хранения запасов равны
![]() руб.
руб.
Наименьшие издержки за год на производство и хранение микросхем будут при условии
![]() .
.
Производная равна
![]() .
.
Отсюда оптимальный размер выпускаемой партии микросхем равен
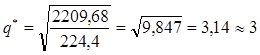 тыс. шт.
тыс. шт.
Количество партий равно
![]() .
.
Периодичность подачи заказа при этом составит
![]() дней.
дней.
Проверим возможность изготовления такой партии. Для этого должно выполняться условие
![]() .
.
Действительно, 3000 < 510 × 11 = 5610, т.е. завод может выпускать такие партии микросхем.
Отсюда годовые издержки завода на производство и хранение микросхем составят
![]() руб.
руб.
2. Закупка микросхем.
Общие организационные издержки в данном случае составят
![]() руб.,
руб.,
Стоимость микросхем равна
![]() руб.
руб.
Общие издержки хранения запасов равны
![]() руб.
руб.
Наименьшие издержки за год на закупку и хранение микросхем будут при условии
![]() .
.
Производная равна
![]() .
.
Отсюда оптимальный размер закупаемой партии микросхем равен
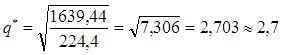 тыс. шт.
тыс. шт.
Количество партий равно
![]() .
.
Периодичность подачи заказа при этом составит
![]() дней.
дней.
Отсюда годовые издержки завода на закупку и хранение микросхем составят
![]() руб.
руб.
Выводы.
Заводу выгоднее закупать микросхемы, чем самому изготавливать. При этом годовые издержки на покупку и хранение микросхем составят 1426,92 руб.
Достигнутая экономия по сравнению с издержками при самостоятельном изготовлении микросхем составляет 1937,23 – 1426,92 = 510,31 руб.