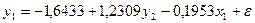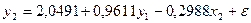Министерство
образования и науки РФ
Федеральное агентство по образованию
Государственное
образовательное учреждение
Высшее
профессиональное образование
Всероссийский
заочный финансово-экономический институт
филиал в г. Туле
КОНТРОЛЬНАЯ РАБОТА
по дисциплине
ЭКОНОМЕТРИКА
Вариант №9
|
Выполнил:
|
|
курс
|
|
факультет
|
|
|
специальность
|
|
группа
|
|
|
№ зачётной
книжки
|
|
|
Руководитель:
|
Арсеньев Ю.Н.
|
Тула, 2007г.
Задание 1.
- Построим линейную модель:

Все вычисления занесем в таблицу:
|
i
|
y
|
x
|
yx
|
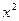
|
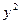
|
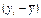
|
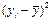
|
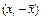
|
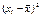
|
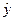
|
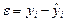
|
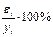
|
|
1
|
21
|
12
|
252
|
144
|
441
|
-2,7
|
7,29
|
-4,1
|
16,81
|
19,73248
|
1,26751908
|
6,04%
|
|
2
|
10
|
4
|
40
|
16
|
100
|
-13,7
|
187,69
|
-12,1
|
146,41
|
11,99098
|
-1,9909803
|
19,91%
|
|
3
|
26
|
18
|
468
|
324
|
676
|
2,3
|
5,29
|
1,9
|
3,61
|
25,53861
|
0,4613936
|
1,77%
|
|
4
|
33
|
27
|
891
|
729
|
1089
|
9,3
|
86,49
|
10,9
|
118,81
|
34,24779
|
-1,2477946
|
3,78%
|
|
5
|
34
|
26
|
884
|
676
|
1156
|
10,3
|
106,09
|
9,9
|
98,01
|
33,28011
|
0,71989295
|
2,12%
|
|
6
|
37
|
29
|
1073
|
841
|
1369
|
13,3
|
176,89
|
12,9
|
166,41
|
36,18317
|
0,81683021
|
2,21%
|
|
7
|
9
|
1
|
9
|
1
|
81
|
-14,7
|
216,09
|
-15,1
|
228,01
|
9,087918
|
-0,0879175
|
0,98%
|
|
8
|
21
|
13
|
273
|
169
|
441
|
-2,7
|
7,29
|
-3,1
|
9,61
|
20,70017
|
0,2998315
|
1,43%
|
|
9
|
32
|
26
|
832
|
676
|
1024
|
8,3
|
68,89
|
9,9
|
98,01
|
33,28011
|
-1,280107
|
4,00%
|
|
10
|
14
|
5
|
70
|
25
|
196
|
-9,7
|
94,09
|
-11,1
|
123,21
|
12,95867
|
1,04133214
|
7,44%
|
|
Итого
|
237
|
161
|
4792
|
3601
|
6573
|
0,00
|
956,10
|
0,00
|
1008,90
|
237,00
|
0,00
|
49,67%
|
|
Ср.значение
|
23,7
|
16,1
|
479,2000
|
360,1
|
657,3
|
|
|
|
|
|
|
4,97%
|
Найдем значения
неизвестных параметров:
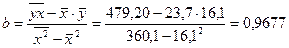
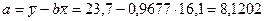
Тогда 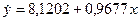 , то есть с увеличением капиталовложений на 1млн.руб. объем
выпускаемой продукции увеличится в среднем на 978 тыс.руб.
, то есть с увеличением капиталовложений на 1млн.руб. объем
выпускаемой продукции увеличится в среднем на 978 тыс.руб.
Коэффициент корреляции: 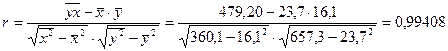
Т.е. связь между объемом капиталовложений и выпускаемой
продукции можно считать прямой и тесной, т.к. 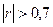
Коэффициент
детерминации: 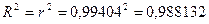 , т.е. вариация
, т.е. вариация  (выпускаемая продукция) на 98,2% объясняется вариацией
фактора
(выпускаемая продукция) на 98,2% объясняется вариацией
фактора  (объем
капиталовложений).
(объем
капиталовложений).
F-критерий Фишера: 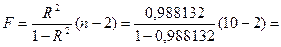 666,1041
666,1041
По таблице для 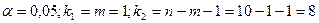 находим, что
находим, что 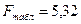 . Так как 190,098>5,32, то уравнение регрессии в целом
статистически значимо.
. Так как 190,098>5,32, то уравнение регрессии в целом
статистически значимо.
Средняя относительная
ошибка: 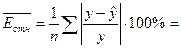 4,97%, т.е. в среднем расчетные значения
4,97%, т.е. в среднем расчетные значения  для линейной модели отличаются от фактических значений на 4,97%.
для линейной модели отличаются от фактических значений на 4,97%.
2.
Построим
степенную модель: 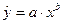 .
.
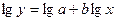
Обозначим: 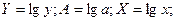 Y=A+bX
Y=A+bX
Все вычисления занесем в таблицу:
|
i
|
y
|
x
|
Y
|
X
|
YX
|
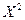
|
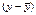
|
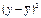
|
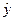
|
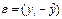
|
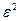
|
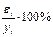
|
|
1
|
21
|
12
|
1,322219295
|
1,079181
|
1,4269
|
1,1646
|
-2,7
|
7,29
|
22,0166
|
-1,016618
|
1,0335118
|
4,84%
|
|
2
|
10
|
4
|
1
|
0,60206
|
0,6021
|
0,3625
|
-13,7
|
187,69
|
13,384
|
-3,384039
|
11,451719
|
33,84%
|
|
3
|
26
|
18
|
1,414973348
|
1,255273
|
1,7762
|
1,5757
|
2,3
|
5,29
|
26,4564
|
-0,45636
|
0,20826428
|
1,76%
|
|
4
|
33
|
27
|
1,51851394
|
1,431364
|
2,1735
|
2,0488
|
9,3
|
86,49
|
31,7914
|
1,208606
|
1,46072813
|
3,66%
|
|
5
|
34
|
26
|
1,531478917
|
1,414973
|
2,167
|
2,0021
|
10,3
|
106,09
|
31,2524
|
2,747571
|
7,54914905
|
8,08%
|
|
6
|
37
|
29
|
1,568201724
|
1,462398
|
2,2933
|
2,1386
|
13,3
|
176,89
|
32,8375
|
4,162516
|
17,3265427
|
11,25%
|
|
7
|
9
|
1
|
0,954242509
|
0
|
0
|
0
|
-14,7
|
216,09
|
7,14199
|
1,858009
|
3,45219559
|
20,64%
|
|
8
|
21
|
13
|
1,322219295
|
1,113943
|
1,4729
|
1,2409
|
-2,7
|
7,29
|
22,8297
|
-1,829681
|
3,34773206
|
8,71%
|
|
9
|
32
|
26
|
1,505149978
|
1,414973
|
2,1297
|
2,0021
|
8,3
|
68,89
|
31,2524
|
0,747571
|
0,55886312
|
2,34%
|
|
10
|
14
|
5
|
1,146128036
|
0,69897
|
0,8011
|
0,4886
|
-9,7
|
94,09
|
14,8079
|
-0,807884
|
0,65267678
|
5,77%
|
|
Итого
|
237
|
161
|
13,28312704
|
10,47314
|
14,843
|
13,024
|
0,00
|
956,10
|
233,77
|
3,23
|
47,04
|
100,89%
|
|
Ср.зна
чение
|
23,7
|
16,1
|
1,328312704
|
1,047314
|
1,4843
|
1,3024
|
0,000000
|
95,61
|
23,377
|
0,322969
|
4,70413825
|
10,09%
|
Найдем значения неизвестных параметров:
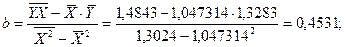
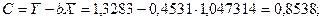
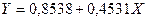
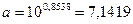
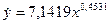
Индекс корреляции: 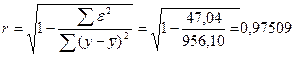
Т.е. связь между объемом капиталовложений и выпускаемой
продукции можно считать тесной, т.к. 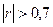
Коэффициент
детерминации: 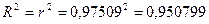 , т.е. вариация
, т.е. вариация  (выпускаемая продукция) на 98,2% объясняется вариацией
фактора
(выпускаемая продукция) на 98,2% объясняется вариацией
фактора  (объем
капиталовложений).
(объем
капиталовложений).
F-критерий Фишера: 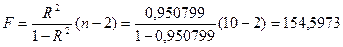
По таблице для 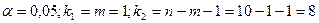 находим, что
находим, что 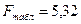 . Так как 154,9737>5,32, то уравнение регрессии в целом
статистически значимо.
. Так как 154,9737>5,32, то уравнение регрессии в целом
статистически значимо.
Средняя относительная
ошибка: 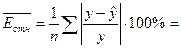 10,09%, т.е. в среднем расчетные значения
10,09%, т.е. в среднем расчетные значения 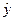 для линейной модели отличаются от фактических значений на 10,09%.
для линейной модели отличаются от фактических значений на 10,09%.
3. Построим
показательную модель: 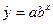
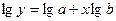
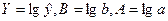 , тогда Y=A+Bx
, тогда Y=A+Bx
Все вычисления занесем в таблицу:
|
i
|
y
|
x
|
Y
|
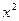
|
Yx
|
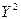
|
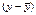
|
 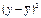
|
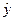
|
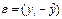
|
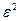
|
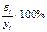
|
|
1
|
21
|
12
|
1,322219295
|
144
|
15,867
|
1,7483
|
-2,7
|
7,29
|
17,5331
|
3,46686
|
12,0191174
|
57,23%
|
|
2
|
10
|
4
|
1
|
16
|
4
|
1
|
-13,7
|
187,69
|
11,997
|
-1,997019
|
3,98808651
|
39,88%
|
|
3
|
26
|
18
|
1,414973348
|
324
|
25,47
|
2,0021
|
2,3
|
5,29
|
23,305
|
2,694981
|
7,26292283
|
27,93%
|
|
4
|
33
|
27
|
1,51851394
|
729
|
41
|
2,3059
|
9,3
|
86,49
|
35,7136
|
-2,713638
|
7,36383272
|
22,31%
|
|
5
|
34
|
26
|
1,531478917
|
676
|
39,818
|
2,3454
|
10,3
|
106,09
|
34,0593
|
-0,059307
|
0,00351728
|
0,01%
|
|
6
|
37
|
29
|
1,568201724
|
841
|
45,478
|
2,4593
|
13,3
|
176,89
|
39,2673
|
-2,267268
|
5,14050202
|
13,89%
|
|
7
|
9
|
1
|
0,954242509
|
1
|
0,9542
|
0,9106
|
-14,7
|
216,09
|
10,4059
|
-1,405872
|
1,97647632
|
21,96%
|
|
8
|
21
|
13
|
1,322219295
|
169
|
17,189
|
1,7483
|
-2,7
|
7,29
|
18,3848
|
2,615239
|
6,83947324
|
32,57%
|
|
9
|
32
|
26
|
1,505149978
|
676
|
39,134
|
2,2655
|
8,3
|
68,89
|
34,0593
|
-2,059307
|
4,24074392
|
13,25%
|
|
10
|
14
|
5
|
1,146128036
|
25
|
5,7306
|
1,3136
|
-9,7
|
94,09
|
12,5797
|
1,42026
|
2,01713937
|
14,41%
|
|
Итого
|
237
|
161
|
13,28312704
|
3601
|
234,64
|
18,099
|
0,00
|
956,10
|
237,31
|
|
50,85
|
243,46%
|
|
Ср.зна
чение
|
23,7
|
16,1
|
1,328312704
|
360,1
|
23,464
|
|
|
|
|
|
|
24,35%
|
Найдем значения неизвестных параметров:
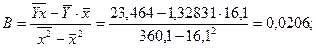
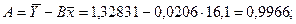
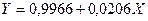
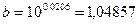
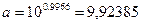
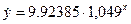
Индекс корреляции: 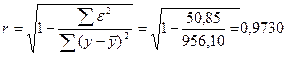
Т.е. связь между объемом капиталовложений и выпускаемой
продукции можно считать тесной, т.к. 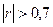
Коэффициент
детерминации: 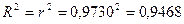 , т.е. вариация
, т.е. вариация 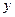 (выпускаемая продукция) на 97,3% объясняется вариацией
фактора
(выпускаемая продукция) на 97,3% объясняется вариацией
фактора 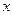 (объем
капиталовложений).
(объем
капиталовложений).
F-критерий Фишера: 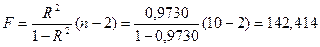
По таблице для 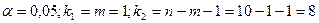 находим, что
находим, что 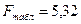 . Так как 142.414 >5,32, то уравнение регрессии в целом
статистически значимо.
. Так как 142.414 >5,32, то уравнение регрессии в целом
статистически значимо.
Средняя относительная
ошибка: 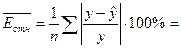 24,35%, т.е. в среднем расчетные значения
24,35%, т.е. в среднем расчетные значения 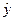 для линейной модели отличаются от фактических значений на 24,35%.
для линейной модели отличаются от фактических значений на 24,35%.
4.
Построим
гиперболическую модель: 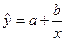
Обозначим через 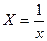 , тогда
, тогда 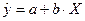
Все вычисления занесем в таблицу:
|
i
|
y
|
x
|
X
|
yX
|
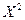
|
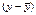
|
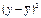
|
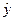
|
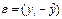
|
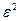
|
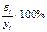
|
|
1
|
21
|
12
|
0,083333333
|
1,75
|
0,0069
|
-2,7
|
7,29
|
26,0266
|
-5,02655
|
25,26624
|
120,32%
|
|
2
|
10
|
4
|
0,25
|
2,5
|
0,0625
|
-13,7
|
187,69
|
22,0735
|
-12,0735
|
145,7705
|
1457,71%
|
|
3
|
26
|
18
|
0,055555556
|
1,444444
|
0,0031
|
2,3
|
5,29
|
26,6854
|
-0,68539
|
0,469757
|
1,81%
|
|
4
|
33
|
27
|
0,037037037
|
1,222222
|
0,0014
|
9,3
|
86,49
|
27,1246
|
5,87539
|
34,52019
|
104,61%
|
|
5
|
34
|
26
|
0,038461538
|
1,307692
|
0,0015
|
10,3
|
106,09
|
27,0908
|
6,90917
|
47,7367
|
140,40%
|
|
6
|
37
|
29
|
0,034482759
|
1,275862
|
0,0012
|
13,3
|
176,89
|
27,1852
|
9,81481
|
96,33042
|
260,35%
|
|
7
|
9
|
1
|
1
|
9
|
1
|
-14,7
|
216,09
|
4,28501
|
4,71499
|
22,23109
|
247,01%
|
|
8
|
21
|
13
|
0,076923077
|
1,615385
|
0,0059
|
-2,7
|
7,29
|
26,1786
|
-5,17859
|
26,81782
|
127,70%
|
|
9
|
32
|
26
|
0,038461538
|
1,230769
|
0,0015
|
8,3
|
68,89
|
27,0908
|
4,90917
|
24,1
|
75,31%
|
|
10
|
14
|
5
|
0,2
|
2,8
|
0,04
|
-9,7
|
94,09
|
23,2594
|
-9,25945
|
85,73739
|
612,41%
|
|
Итого
|
237
|
161
|
1,814254838
|
24,14637
|
1,124
|
0,00
|
956,10
|
237,00
|
0,00
|
508,98
|
3147,63%
|
|
Ср.
значение
|
23,7
|
16,1
|
0,181425484
|
2,414637
|
0,1124
|
|
|
|
|
|
314,76%
|
Найдем значения неизвестных параметров:
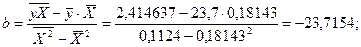
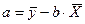 =23,7-23,7154*0,18143=28,0031
=23,7-23,7154*0,18143=28,0031
Тогда 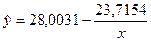
Индекс корреляции: 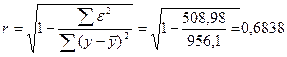
Т.е. связь между объемом капиталовложений и выпускаемой
продукции можно считать тесной, т.к. 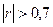
Коэффициент
детерминации: 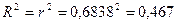 , т.е. вариация
, т.е. вариация 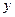 (выпускаемая продукция) на 46,7% объясняется вариацией
фактора
(выпускаемая продукция) на 46,7% объясняется вариацией
фактора 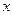 (объем
капиталовложений).
(объем
капиталовложений).
F-критерий Фишера: 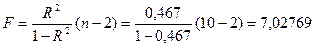
По таблице для 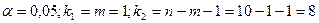 находим, что
находим, что 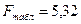 . Так как 7,02769 >5,32, то уравнение регрессии в целом
статистически значимо.
. Так как 7,02769 >5,32, то уравнение регрессии в целом
статистически значимо.
Средняя относительная
ошибка: 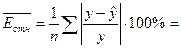 314,76%, т.е. в среднем расчетные значения
314,76%, т.е. в среднем расчетные значения  для линейной модели отличаются от фактических значений на 314,76%.
для линейной модели отличаются от фактических значений на 314,76%.
|
Сводная
таблица
|
|
|
|
|
|
Параметры Модель
|
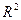
|
F-критерий
Фишера
|
r
|
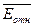
|
|
Линейная
|
0.988132397
|
666.1041196
|
0.99404849
|
4.97%
|
|
Степенная
|
0.950798679
|
154.597262
|
0.97508906
|
10.09%
|
|
Показательная
|
0.946813292
|
142.4135204
|
0.97304331
|
24.35%
|
|
Гиперболическая
|
0.467649679
|
7.027698282
|
0.68384916
|
314.76%
|
|
|
|
|
|
|
|
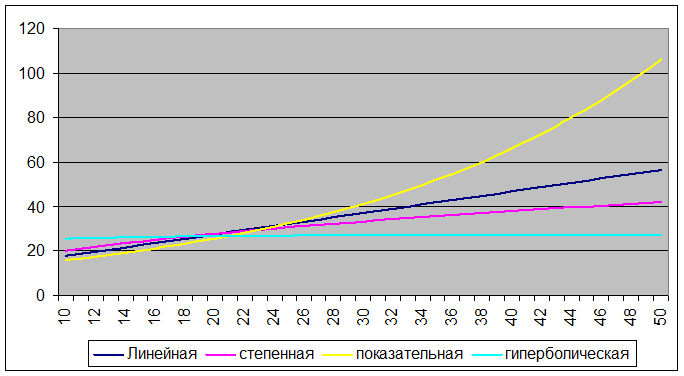
Таким образом, наилучшей моделью оказалась – линейная.
Построим прогноз.
Согласно исходным данным 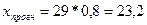 , тогда
, тогда
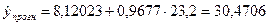 млн.руб
млн.руб
Найдем верхнюю 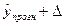 и нижнюю
и нижнюю 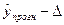 границы прогноза, где
границы прогноза, где
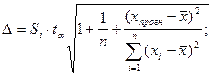
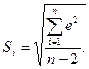
Получаем: 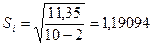 ;
;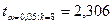 и
и 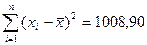 , тогда
, тогда
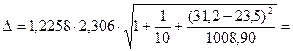 2,94503
2,94503
Нижняя граница: 30,4706 - 2,94503 = 27,6256
Верхняя граница: 30,4706 - 2,94503 = 33,5156
Задание 2.
Задача 2а:
Исходные данные:
|
Номер уравнения
|
Переменные
|
|
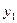
|
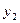
|
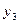
|
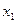
|
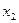
|
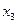
|
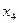
|
|
1
|
-1
|
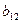
|
0
|
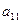
|
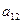
|
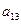
|
0
|
|
2
|
0
|
-1
|
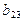
|
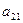
|
0
|
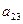
|
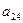
|
|
3
|
0
|
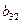
|
- 1
|
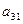
|
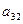
|
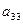
|
0
|
На основе исходных данных запишем систему одновременных
уравнений:
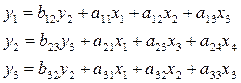 (1)
(1)
Проверим каждое уравнение системы (1) на выполнение
необходимого и достаточного условия идентификации.
В первом уравнении
две эндогенные переменные: 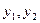 (H=2). В нем отсутствует экзогенная
переменная:
(H=2). В нем отсутствует экзогенная
переменная: 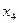 (D=1). Необходимое условие идентификации D+1=H выполнено.
(D=1). Необходимое условие идентификации D+1=H выполнено.
Для проверки на достаточное условие составим матрицу из
коэффициентов при переменной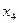 :
:
|
Уравнение
|
Отсутствующие
переменные
|
|
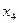
|
|
2
|
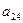
|
|
3
|
0
|
Определитель матрицы равен нулю. Значит, достаточное условие
не выполнено, и первое уравнение нельзя считать идентифицируемым.
Следовательно, исследуемая система неидентифицируема,
так как первое уравнение системы неидентифицируемо.
Задача 2б:
Исходные данные:
|
Номер уравнения
|
Переменные
|
|
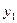
|
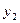
|
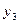
|
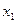
|
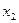
|
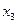
|
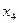
|
|
1
|
-1
|
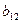
|
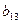
|
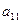
|
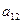
|
0
|
0
|
|
2
|
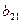
|
-1
|
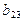
|
0
|
0
|
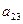
|
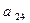
|
|
3
|
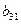
|
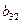
|
-1
|
0
|
0
|
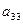
|
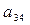
|
На основе исходных данных запишем систему одновременных
уравнений:
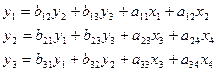 (1)
(1)
Проверим каждое уравнение системы (1) на выполнение
необходимого и достаточного условия идентификации.
В первом уравнении
три эндогенные переменные: 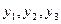 (H=3). В нем отсутствуют экзогенные
переменные:
(H=3). В нем отсутствуют экзогенные
переменные: 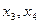 (D=2). Необходимое условие идентификации D+1=H выполнено.
(D=2). Необходимое условие идентификации D+1=H выполнено.
Для проверки на достаточное условие составим матрицу из коэффициентов
при переменных 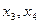 :
:
|
Уравнение
|
Отсутствующие
переменные
|
|
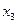
|
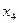
|
|
2
|
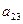
|
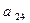
|
|
3
|
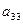
|
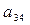
|
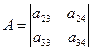 - матрица
коэффициентов
- матрица
коэффициентов
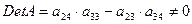
Определитель матрицы не равен нулю, ранг матрицы равен 2;
следовательно, выполняется достаточное условие идентификации, и первое
уравнение точно идентифицируемо.
Во втором уравнении
три эндогенные переменные: 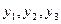 (H=3). В нем отсутствуют экзогенные
переменные:
(H=3). В нем отсутствуют экзогенные
переменные: 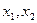 (D=2). Необходимое условие идентификации D+1=H выполнено.
(D=2). Необходимое условие идентификации D+1=H выполнено.
Для проверки на достаточное условие составим матрицу из
коэффициентов при переменных 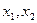 :
:
|
Уравнение
|
Отсутствующие
переменные
|
|
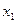
|
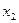
|
|
1
|
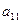
|
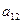
|
|
3
|
0
|
0
|
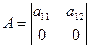 - матрица
коэффициентов
- матрица
коэффициентов
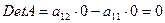
Определитель матрицы равен нулю. Значит, достаточное условие
не выполнено, и второе уравнение нельзя
считать идентифицируемым.
Следовательно, исследуемая система неидентифицируема,
так как второе уравнение системы не идентифицируемо.
Задача 2в:
Используя метод наименьших
квадратов, построить структурную модель вида:
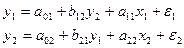
Исходные данные:
|
n
|
|
|
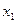
|
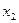
|
|
1
|
25,1
|
21,8
|
8
|
7
|
|
2
|
41,7
|
33,8
|
10
|
14
|
|
3
|
12,5
|
12,5
|
7
|
1
|
|
4
|
25,9
|
23,4
|
7
|
8
|
|
5
|
41,7
|
36,0
|
5
|
17
|
|
6
|
9,4
|
11,4
|
2
|
2
|
|
Сумма
|
156,3
|
138,9
|
39
|
49
|
|
Ср.знач.
|
26,05
|
23,5
|
6,5
|
8,166
|
Структурную модель преобразуем в
приведенную форму модели:
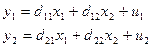
Где 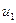 и
и 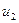 - случайные ошибки.
- случайные ошибки.
Для каждого уравнения приведенной
формы при расчете коэффициентов 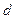 можно применить МНК.
можно применить МНК.
Для упрощения расчетов можно
работать с отклонениями от средних уровней 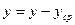 и
и 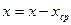 (
(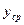 и
и 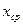 - средние значения). Преобразованные таким образом исходные
данные сведены в таблице:
- средние значения). Преобразованные таким образом исходные
данные сведены в таблице:
|
n
|
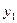
|
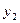
|
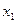
|
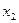
|
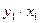
|
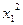
|
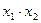
|
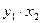
|
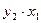
|
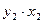
|
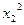
|
|
1
|
25,1
|
21,8
|
8
|
7
|
200,8
|
64
|
56
|
175,7
|
174,4
|
152,6
|
49
|
|
2
|
41,7
|
33,8
|
10
|
14
|
417
|
100
|
140
|
538,8
|
338
|
473,3
|
196
|
|
3
|
12,5
|
12,5
|
7
|
1
|
87,5
|
49
|
7
|
12,5
|
87,5
|
12,5
|
1
|
|
4
|
25,9
|
23,4
|
7
|
8
|
181,3
|
49
|
56
|
207,2
|
163,8
|
187,2
|
64
|
|
5
|
41,7
|
36,0
|
5
|
17
|
208,5
|
25
|
85
|
708,9
|
180
|
612
|
289
|
|
6
|
9,4
|
11,4
|
2
|
2
|
18,8
|
4
|
4
|
18,8
|
22,8
|
22,8
|
4
|
|
Сумма
|
156,3
|
138,9
|
39
|
49
|
1113,9
|
291
|
348
|
1706,9
|
966,5
|
1460,3
|
603
|
|
Ср.знач.
|
26,05
|
23,5
|
6,5
|
8,166
|
185,65
|
48,5
|
58
|
284,483
|
161,038
|
243,383
|
100,5
|
Для нахождения коэффициентов 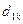 первого приведенного
уравнения можно использовать следующую систему нормальных уравнений:
первого приведенного
уравнения можно использовать следующую систему нормальных уравнений:
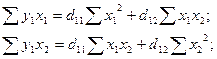
Подставляя рассчитанные в таблице
значения сумм, получим:
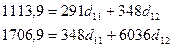
Решение этих уравнений дает
значения 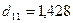 и
и 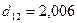
Первое уравнение приведенной
формы имеет вид:
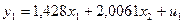
Для нахождения коэффициентов 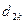 второго приведенного
уравнения можно использовать следующую систему нормальных уравнений:
второго приведенного
уравнения можно использовать следующую систему нормальных уравнений:
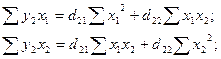
Подставляя рассчитанные в таблице
значения сумм, получим:
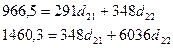
Решение этих уравнений дает
значения 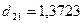 и
и 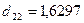
Второе уравнение приведенной
формы модели примет вид:
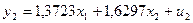
Для перехода от приведенной формы
к структурной форме модели найдем 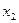 из второго уравнения приведенной формы модели:
из второго уравнения приведенной формы модели:
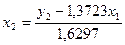
Подставим это выражение в первое
уравнение приведенной модели, найдем структурное уравнение:
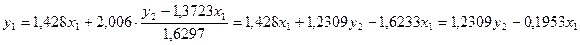
Таким образом, 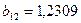 ,
, 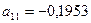
Найдем 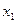 из первого уравнения
приведенной формы модели:
из первого уравнения
приведенной формы модели:
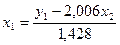
Подставим это выражение во второе
уравнение приведенной модели, найдем структурное уравнение:
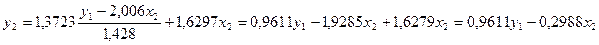
Таким образом,  ,
, 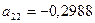
Свободные члены структурной формы
находим из уравнений:
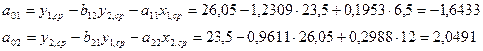
Окончательный вид структурной
модели: