Содержание
Введение. 3
Модели прогнозирования как часть системы поддержки принятия решений 4
Практическая часть. 12
Заключение. 14
Список использованной литературы.. 15
Введение
Моделирование предполагает конструирование модели на основе предварительного изучения объекта или процесса, выделения его существенных характеристик или признаков. Прогнозирование экономических и социальных процессов с использованием моделей включает разработку модели, ее экспериментальный анализ, сопоставление результатов прогнозных расчетов на основе модели с фактическими данными состояния объекта или процесса, корректировку и уточнение модели.
В зависимости от уровня управления экономическими и социальными процессами различают макроэкономические, межотраслевые, межрайонные, отраслевые, региональные модели и модели развития фирмы.
По аспектам развития экономики выделяют модели прогнозирования воспроизводства основных фондов, трудовых ресурсов, цен и др. Существует ряд других признаков классификации моделей: временной, факторный, транспортный, производственный.
Цель работы – рассмотреть модели прогнозирования как часть системы поддержки принятия решений.
Задачи работы – на основе полученных основных сведений в процессе изучения специальной литературы, данных периодических источников и Интернет, рассмотреть модель оптимального планирования, изучить систему экономико-математических моделей.
Модели прогнозирования как часть системы поддержки принятия решений
В современных условиях в стране развитию моделирования и практическому применению моделей стала придаваться особая значимость в связи с усилением роли прогнозирования и переходом к индикативному планированию.[1]
Рассмотрим некоторые из наиболее разработанных экономико-математических моделей, получивших широкое применение в практике прогнозирования экономики за рубежом и используемых в странах СНГ.
К матричным моделям относятся модели межотраслевого баланса (МОБ): статические и динамические. Первые предназначены для проведения прогнозных макроэкономических расчетов на краткосрочный период (год, квартал, месяц), вторые - для расчетов развития экономики страны на перспективу. Они отражают процесс воспроизводства в динамике и обеспечивают увязку прогноза производства продукции (услуг) с инвестициями.
Сформированный на основе моделей межотраслевой баланс может использоваться для решения многих задач: прогнозирования макроэкономических показателей, межотраслевых связей и потоков (поставок), структуры экономики, отраслевых издержек, динамики цен, показателей эффективности производства (материало-, энерго-, металло-, химико- и фондоемкости)[2].
Модели оптимального планирования используются для определения оптимального варианта функционирования экономики в целом и ее отдельных звеньев.
Экономико-математическая модель представляет собой формализованное описание экономического процесса и состоит из целевой функции и системы ограничений. Целевая функция описывает цель оптимизации и представляет собой зависимость показателя, по которому ведется оптимизация, от независимых переменных. Влияние каждой из переменных на величину целевой функции выражается коэффициентом - значением показателя, экстремум которого используется в качестве критерия оптимальности. Система ограничений отражает объективные экономические связи и зависимости и представляет собой систему равенств и неравенств. На макроуровне критерием оптимальности является максимум валового национального продукта. На микроуровне в качестве критерия оптимальности могут быть использованы экстремумы показателей: максимум прибыли, минимум затрат, максимум выпуска продукции или услуг и др.
Следует отметить, что, несмотря на многообразие разработанных моделей и наличие пакетов программ для проведения многовариантных расчетов, оптимизационные задачи в республике носят, как правило, экспериментальный характер. Главными причинами, сдерживающими их внедрение в практику прогнозных и плановых расчетов как на макро-, так и на микроуровне, являются:
а) неадекватность разрабатываемых моделей реальным экономическим процессам;
б) отсутствие специалистов-практиков, хорошо владеющих моделированием экономических и социальных процессов и методами оптимизации;
в) проблема информационного обеспечения.
Экономико-статистические модели используются для установления количественной характеристики связи, зависимости и взаимообусловленности экономических показателей. Система такого рода моделей включает: одно-, многофакторные и эконометрические модели.
Многофакторные модели позволяют одновременно учитывать воздействие нескольких факторов на уровень прогнозируемого показателя. Данные модели используются при прогнозировании макроэкономических показателей, показателей спроса на продукцию, себестоимости, цен, прибыли и др.[3]
Эконометрической моделью называют систему регрессионных уравнений и тождеств, описывающих взаимосвязи и зависимости основных показателей развития экономики. Система экономико-математических моделей эконометрического типа служит для описания сложных социально-экономических процессов. Факторы (переменные) эконометрической модели подразделяются на экзогенные (внешние) и эндогенные (внутренние). Экзогенные переменные выбираются так, чтобы они оказывали влияние на моделируемую систему, а сами ее влиянию не подвергались. Они могут вводиться в модель на основе экспертных оценок. Эндогенные переменные определяются путем решения стохастических и тождественных уравнений. Для каждой эндогенной переменной методом наименьших квадратов оценивается несколько вариантов регрессионных уравнений и выбирается лучший для включения в модель.
Например, инвестиции производственного назначения зависят от суммы прибыли (эндогенный фактор) и индекса цен на инвестиционные товары (экзогенный фактор). Органичной частью эконометрической модели может быть и межотраслевой баланс. Обычно количество уравнений модели равно количеству эндогенных переменных.
Термин "сетевое планирование" приобретает в последнее время большую популярность. Основой сетевого планирования служит изображение комплекса взаимосвязанных работ в виде графа, обычно именуемого сетевым графиком, стрелочной диаграммой, логической сетью или сетевой моделью. В сетевом графике отражается последовательность этапов планирования, необходимых для достижения заранее поставленной цели.
Примером сетевых методов планирования является метод ПЕРТ-время, или ПЕРТ-затраты.
Экономико-математические модели могут быть реализованы с помощью экономико-математических методов (ЭММ). ЭММ представляют собой способы (приемы) расчета экономических показателей с применением методов прикладной математики и математической статистики. С помощью ЭММ появляется возможность всестороннего обоснования изменения экономических показателей. Они позволяют повышать качество прогнозов, осуществлять многовариантные оптимизационные расчеты.
Среди важнейших экономико-математических методов, используемых в прогнозировании и планировании экономических и социальных процессов как в нашей стране, так и за рубежом, следует выделить: метод межотраслевого баланса, методы оптимизации (симплекс-метод и др.), корреляционно-регрессионный метод.
Построение математической модели прогнозирования поведения является трудной задачей в связи с сильным влиянием политических и других проблем (выборы, природные катаклизмы, спекуляции крупных участников рынка…).
В основе модели лежит анализ некоторых критериев с последующим выводом о поведении доходности и ценовых показателей. В набор критериев входят различные макро- и микроэкономические показатели, информация с торговых площадок, экспертные оценки специалистов. Процедура прогнозирования состоит из этапов:
Подготовка и предварительная фильтрация данных;
Аппроксимация искомой зависимости линейной функцией;
Моделирование погрешности с помощью линейной сети.
Но для повышения точности модели практикуется нелинейный анализ с использованием многослойной однородной нейронной сети. Этапы проведения нелинейного анализа в системе совпадают со стандартными шагами при работе с нейросетями.
1-й этап. Подготовка выходных данных.
Выходными данными являются zi = yi-pi, где yi - реальное значение прогнозируемой величины на некоторую дату, pi - рассчитанное на эту дату с помощью линейного анализа.
2-й этап. Нормирование входных сигналов.
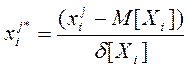 (1)
(1)
где xij - j-я координата некоторого критерия Xi, M[Xi] - выборочная оценка среднего квадратичного отклонения.
3-й этап. Выбор функции активации и архитектуры нейронной сети.
Используются функции активации стандартного вида (сигмоидная, ступенчатая), а также следующего вида:
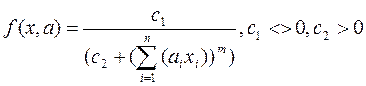 (2)
(2)
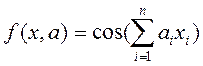 (3)
(3)
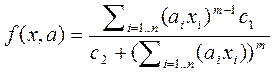 (4)
(4)
 (5)
(5)
Архитектура нейронной сети представлена на рисунке:
|
|
вектор
![]()
![]()
![]() входных
входных
|
![]()
выходн.
![]()
|
|
![]()
![]() входных
входных
сигналов
Введены следующие обозначения: Sj - линейные сумматоры; fj - нелинейные функции; используемые для аппроксимации; S - итоговый сумматор.
4-й этап. Выбор алгоритма обучения нейронной сети, основанного на одном из следующих методов: обратного распространения ошибки, градиентного спуска, метода сопряженных градиентов, методе Ньютона, квазиньютоновском. Методы оцениваются по времени, затрачиваемому на обучение и по величине погрешности.
5-й этап. Итоговые вычисления границ прогнозируемого значения:
P=Pлин+Рнелин±Енелин
где Р — итоговое прогнозируемое значение, Рлин и Рнелин значение линейного и нелинейного анализов. Енелин — погрешность полученная на этапе нелинейного анализа.[4]
Результаты задачи прогнозирования используются в построенной на ее основе задаче оптимального управления инвестиционным портфелем. В основе разработанной задачи управления идея минимизации трансакционных издержек по переводу портфеля в класс оптимальных.
Используемый поход основан на предположениях, что эффективность инвестирования в некий набор активов является реализацией многомерной случайной величины, математическое ожидание которой характеризует доходность (m={mi}i=1..n, где mi=M[Ri], i=1..n), матрица ковариаций — риск (V=(Vij), i,j=1..n, где Vij=M[(Ri-mi)(Rj-mj)],i,j=1..n). Описанные параметры (m,V) представляют собой оценку рынка и являются либо прогнозируемой величиной, либо задаются экспертно. Каждому вектору Х, описывающему относительное распределение средств в портфеле, можно поставить в соответствие пару оценок: mx=(m,x), Vx=(Vx,x). Величина mx представляет собой средневзвешенную доходность портфеля, распределение средств в котором описывается вектором Х величина Vх (вариация портфеля [3,5]) является количественной характеристикой риска портфеля х. Введем в рассмотрение оператор Q, действующий из пространства Rn в пространство R2 (критериальная плоскость [3]), который ставит в соответствие вектору х пару чисел (mx, Vx):
Q: Rn-R2 Û "xÌRn, x®((m,x),(Vx,x)). (7)
В задаче управления допустимыми считаются только стандартные портфели, т.е. так называемые портфели без коротких позиций. Правда это накладывает на вектор х два ограничения: нормирующее условие (е,х)=1, где е – единичный вектор размерности n, и условие неотрицательности доли в портфеле, х>=0. Точки удовлетворяющие этим условиям образуют dв пространствеRn так называемый стандартный (n-1)-мерный симплекс. Обозначим его D.
D={xÌRn½(e,x)=1, x³0}
Образом симплекса в критериальной плоскости будет являться замкнутое ограниченное множество оценок допустимых портфелей. Нижняя граница этого множества представляет собой выпуклую вниз кривую, которая характеризует Парето – эффективный с точки зрения критериев выбор инвестора (эффективная граница [3], [5]). Прообразом эффективной границы в пространстве Rn будет эффективное множество портфелей [5]. Обозначим его как y. Данное множество является выпуклым: линейная комбинация эффективных портфелей также представляет собой эффективный портфель [3].
Пусть в некоторый момент времени у нас имеется портфель, распределение средств в котором описывается вектором х. Тогда задачу управления можно сформулировать в следующем виде: найти такой элемент y, принадлежащий y, что r(y,x). Иными словами, для заданной точки х требуется найти ближайший элемент y, принадлежащий множеству Y. В пространстве Rn справедлива теорема, доказывающая существование и единственность элемента наилучшего приближения х элементами множества Y[6]. Метрика (понятие расстояния) может быть введена следующим образом:
r(x,y)=aSi=1,nsup(yi-xi,0)+bSi=1..nsup(xi-yi,0), (9)
где a>0 — относительная величина издержек при покупке, b>0 — относительная величина издержек при продаже актива.[5]
Практическая часть
Задание:
1. Создать базу данных «Заказы» в соответствии с Приложением 3, установить связи.
2. Создать запросы к базе данных для оперативного получения информации по следующим вопросам:
a. Как связаться с нашими клиентами в Сочи?
b. Кто из новосибирских клиентов размещал у нас заказы в марте 2002 г.?
c. Сколько заявок удовлетворено в феврале 2002 г.?
Решение:
База данных «Заказы» была создана средствами СУБД Microsoft Access.
База данных в соответствии с заданием содержит три таблицы: Города, Заказы, Клиенты.
Схема связей между таблицами представлена на рисунке 1.
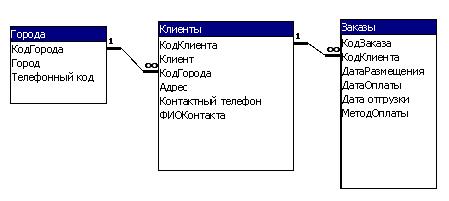
Рисунок 1. Схема базы данных
Связи между таблицами имеют тип «один ко многим». Это означает, что в одном городе может быть много клиентов, а каждый клиент может размещать множество заказов.
Также на рисунке 1 видно, какие поля содержит каждая база данных.
Пример набора данных для таблицы Клиенты приведен ниже.
|
КодКлиента |
Клиент |
КодГорода |
Адрес |
Контактный телефон |
ФИОКонтакта |
|
2 |
ООО универсам "Центральный" |
4 |
ул. Весенняя, 134 |
22-33-78 |
Иванов А.С. |
|
3 |
ЧП "Успех" |
3 |
ул. Октябрьская 286, оф.331 |
25-25-88 |
Сидоров Н.Н. |
|
4 |
ООО магазин "Техника для дома" |
8 |
Курортный проспект, 22 |
33-10-01 |
Соколова А.В. |
|
5 |
АО "Все для кухни" |
1 |
ул. Профсоюзная, 55 |
238-55-98 |
Андреева О.И. |
|
6 |
ЗАО "Фортуна" |
3 |
ул. Московская, 220, оф. 721 |
93-12-00 |
Павлов И.И. |
|
7 |
ЧП Логунова |
3 |
ул. Тимирязева, 2, оф. 102 |
44-33-11 |
Логунов А.И. |
|
8 |
ЧП "Уют" |
8 |
ул. Ленина, 290 |
37-21-02 |
Артемьева Г.И. |
|
9 |
ЗАО маг. "Бытовая техника" |
12 |
пл. Мужества, 21 |
221-18-97 |
Яковлев А.А. |
Код SQL запроса по клиентам в Сочи выглядит следующим образом:
SELECT Города.Город, Клиенты.Клиент, Клиенты.Адрес, Города.[Телефонный код], Клиенты.[Контактный телефон], Клиенты.ФИОКонтакта
FROM Города INNER JOIN Клиенты ON Города.КодГорода = Клиенты.КодГорода
WHERE (((Города.КодГорода)=8));
Код SQL запроса о новосибирских клиентах приведен ниже.
SELECT Клиенты.Клиент, Клиенты.Адрес, Города.[Телефонный код], Клиенты.[Контактный телефон], Клиенты.ФИОКонтакта, Заказы.ДатаРазмещения
FROM (Города INNER JOIN Клиенты ON Города.КодГорода = Клиенты.КодГорода) INNER JOIN Заказы ON Клиенты.КодКлиента = Заказы.КодКлиента
WHERE (((Заказы.ДатаРазмещения)>#3/1/2002#) AND ((Клиенты.КодГорода)=3));
Код SQL запроса о заявках в феврале 2002 г.:
SELECT Клиенты.Клиент, Клиенты.Адрес, Клиенты.[Контактный телефон], Клиенты.ФИОКонтакта, Заказы.ДатаРазмещения, Заказы_1.ДатаОплаты
FROM Клиенты INNER JOIN (Заказы INNER JOIN Заказы AS Заказы_1 ON Заказы.ДатаРазмещения = Заказы_1.ДатаОплаты) ON Клиенты.КодКлиента = Заказы.КодКлиента;
Таким образом, поставленная задача выполнена.
Заключение
Эконометрические модели позволяют прогнозировать широкий круг показателей (ВНП, доходы населения, потребление товаров и услуг и др.). В условиях автоматизации расчетов создается возможность разработки альтернативных вариантов развития экономики с учетом изменений внешних и внутренних условий. Следует отметить, что использование эконометрических моделей требует создания банков данных и подготовки высококвалифицированных специалистов по разработке и реализации этих моделей.
Цель имитационного моделирования состоит в воспроизведении поведения исследуемой системы на основе результатов анализа наиболее существенных взаимосвязей между ее элементами. Имитационные модели позволяют воспроизводить реальные процессы и предвидеть результаты различных действий. Например, имитационную модель оптимизационного процесса можно представить как систематическое изменение значений управляемых переменных с последующим получением результатов прогноза и их анализа.
Модели принятия решений основываются на теории игр и применяются в условиях неопределенности или в ситуациях, когда интересы сторон не совпадают. Каждая из сторон принимает такие решения, т.е. выбирает такую стратегию действий, которая с их точки зрения обеспечивает наибольший выигрыш или наименьший проигрыш. Причем каждой из сторон ясно, что результат зависит не только от собственных действий, но и от действий партнеров. Например, противоборство конкурентов в процессе борьбы за рынок сбыта конкретного вида продукции.
Модели сетевого планирования применяются с целью сокращения сроков выполнения сложных проектов и других работ и оптимального использования предназначенных для этого ресурсов.
Практическая часть работы содержится в прилагаемом mdb файле.
Список использованной литературы
1. Аппак М.А. Автоматизированные рабочие места на основе персональных ЭВМ.- М.: Радио и связь, 1989.-176 с.: ил.
2. Владимирова Л.П. «Прогнозирование и планирование в условиях рынка» Учебное пособие, М., 2003г.
3. Герасенко В.П. «Прогнозирование и планирование экономики», Минск, 2001г.
4. Ивлиев С.В. Всероссийская студенческая конференция «Актуальные проблемы экономики России»: Сб.тез.докл. Воронеж, 2000.
5. http://yandex.ru – Поисковая система
[1] «Прогнозирование и планирование в условиях рынка» Учебное пособие, Л.П. Владимирова, М., 2000г. – стр. 50
[2] Аппак М.А. Автоматизированные рабочие места на основе персональных ЭВМ.- М.: Радио и связь, 1989.-176 с.: ил.
[3] «Прогнозирование и планирование экономики» В.П. Герасенко, Минск, 2001г. – стр. 68
[4] Ивлиев СВ Модель оптимального управления портфелем ценных бумаг. Всероссийская студенческая конференция «Актуальные проблемы экономики России»: Сб.тез.докл. Воронеж, 2000.
[5] Ивлиев СВ Модель прогнозирования рынка ценных бумаг. 6-я Всероссийская студенческая конференция «Актуальные проблемы экономики России»: Сб.тез.докл. Воронеж, 2000.