О Т Ч Е Т

о результатах выполнения

компьютерной лабораторной работы №2

по предмету  «Экономико- математические методы и прикладные модели»

Вариант №1

Выполнил Барзова Т.В.

Специальность Финансы и кредит

Группа Дневная  Курс III

№ зачетной книжки 08ФФД40351

Проверил Филонова Елена Сергеевна

Орел, 2009 г.

ЗАДАНИЕ II

1. Условие задачи

Компания, занимающаяся ремонтом автомобильных дорог, в следующем месяце будет проводить ремонтные работы на пяти участках автодорог. Песок на участки ремонтных работ может доставляться из трех карьеров, месячные объемы  предложений по карьерам известны. Из планов производства ремонтных работ известны месячные объемы потребителей по участкам работ. Имеются экономические оценки транспортных задач (в у.е.) на перевозку 1 тонны песку на ремонтные участки.

Числовые данные для решения :

Матрица планирования

Требуется:

1. Предложить план перевозки песка на участки ремонта автодорог, который обеспечивает минимальные совокупные транспортные издержки.

2. Определить, что произойдет с оптимальным планом, если изменятся условия перевозок: а) появится запрет на перевозки от первого карьера до второго участка работ; б) по этой коммуникации будет ограничен объем перевозок 3 тоннами.

2. Отчет по решению

В данной задаче суммарные потребности равны суммарным запасам:

∑ ³_i=1 a_i= ∑ ⁵_j=1 b_j

25+10+20+30+15=40+20+40

100=100, транспортная задача, в которой суммарные запасы и суммарные потребности совпадают- задача является закрытой.

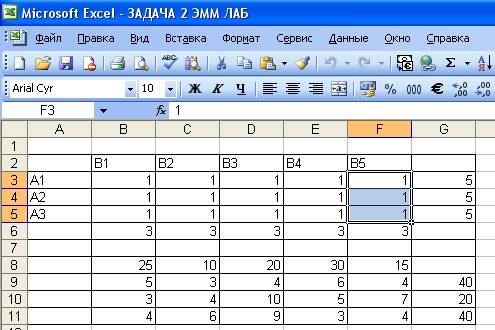
1. Вводим исходные данные.

2. Создаем формы для решения задачи- создаем матрицу перевозок. Для этого обозначаем место, где место где после решения задачи  будет находиться распределение поставок, обеспечивающее минимальные материальные затраты на перевозку груза изменяемые ячейки В3:F5- в них будет записан оптимальный план перевозок х_ij.

3. Вводим условия реализации карьеров

- поместим курсор в ячейку G3 ;

- выбрать знак ∑;

- выделить ячейки B3:F3;

- нажать ENTER для подтверждения ввода формулы для суммирования.

Аналогичные действия выполняем для  ячеек G4, G5.

4. Вводим условия удовлетворения предложения. Для этого необходимо выполняем следующие операции:

- поместим курсор в ячейку В6;

- выбрать знак ∑, при этом автоматически выделяется весь столбец В3:В5;

- нажать ENTER .

Эту же последовательность выполнить для ячеек С6, D6, E6, F6.

5. Назначение целевой ячейки, для этого необходимо произвести следующие действия:

- поместить курсор в ячейку А14;

- запустить «Мастер функции»;

- в окне категория выбрать Математические→СУММПРОИЗВ и нажать кнопку «ОК»;

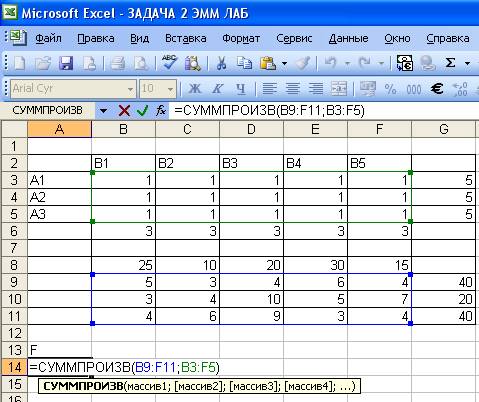
- в окне СУММПРОИЗВ указать адреса массивов, элементы которых обрабатываются этой функций:

- в поле «Массив 1» введем  В9: F11;

- в поле «Массив 2» введем В3: F5;

- нажать кнопку «ОК»

6. ввод зависимостей от математической модели.

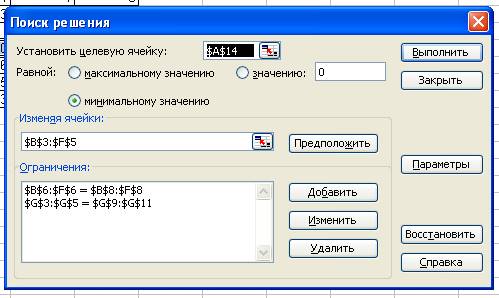
Для этого необходимо выполнить следующие действия:

- выбрать «Сервис»→ «Поиск решения»;

-поместить курсор в поле «Установить целевую (ячейку), ввести адрес $А$14;

- установить направление изменения целевой функции, равное минимальному значению;

- ввести адреса изменяемых ячеек $B$3:$E$6 .

7. Ввод ограничений задачи.

Для этого необходимо:

- выбрать «Добавить ограничения»;

- в поле «Ссылка на ячейку» внести адреса $G$3:$G$5;

- в среднем окне установить знак «=».

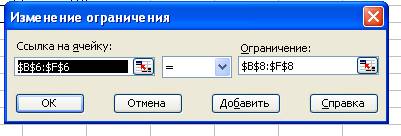
- в поле «Ограничение» установить адреса $G$9:$G$11→кнопка «ОК».

Далее водится ограничения для потребителей:

- выбрать «Добавить ограничение»;

- в поле «Ссылка» на ячейку ввести адреса $B$6:$F$6, в поле знака выбрать знак «=»,→в поле «Ограничений» установить адреса $B$8:$F$8→кнопка «ОК».

-после этого надо вернуться в «Поиск решений»

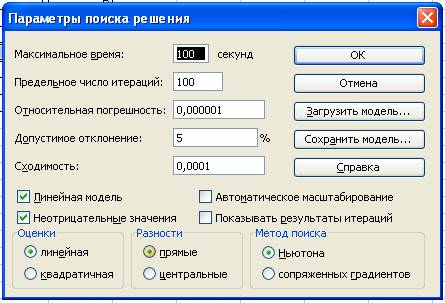
8. Ввод параметров .

- нажимаем окно «Параметры», отмечаем галочками : Линейная модель и неотрицательные значения → нажать кнопку «ОК».

- нажать кнопку «Выполнить»

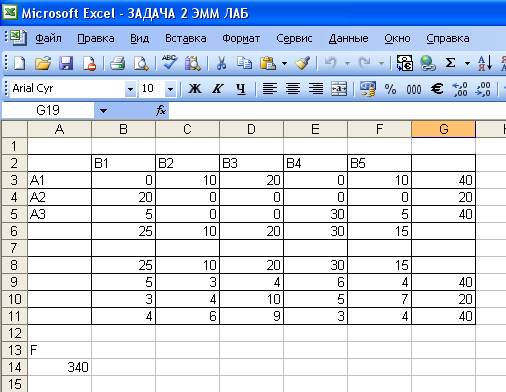
3.Экономические выводы

План перевозки означает, что с первого карьера перевозка песка составит по 10 тонн для 2-го и 5-го участков, а на 3-ий участок выведут 20 тонн; со второго карьера песок вывезут только на 1-ый участок в количестве 20 тонн; с третьего карьера перевозка песка составит по 5 тонн для 1-го и 5-го участков, а на 4-ий участок выведут 30 тонн. Также можно сказать, что на 2-ой и третий участки выгодно перевозить песок только с первого карьера, а на 4-ый участок выгодно перевозить песок только с третьего карьера.  При этом все потребности в песке будут удовлетворены, а общие минимальные транспортные издержки составят 340 у.е

4. Дополнительные условия

А) При изменении условий задачи, в связи с запретом на перевозки от первого карьера к второму участку работ- увеличение перевозки 1 тонны до 1000 у.е., решение измениться в худшую сторону- минимальные совокупные издержки возрастут до 365 у.е, также изменяться условия перевозок на 1-ом и 2-ом участках. На 1-ый участок будет поставляться песок в количестве 5 тонн с первого карьера, и по 10 тонн со второго и третьего карьером.

Б) При ограничении  объемов перевозки 3 тоннами на 2-ой участок с третьего карьера также измениться решение   в худшую сторону - минимальные совокупные издержки возрастут до 365 у.е, также изменяться условия перевозок на 1-ом, 2-ом и 5-ом  участках.