Содержание
Содержание. 2
5. Методика количественных выборочных
исследований. 3
33. Индексный метод и его использование в экономическом анализе. 7
Список литературы.. 14
5. Методика
количественных выборочных исследований
Методика количественных
выборочных исследований отличается от методики качественных исследований
методами оценки рисков, методами планирования выборки, интерпретация
результатов, что обусловлена большей по сравнению с качественными
исследованиями изменчивостью объектов.
Выборочные риски. Часто
при выполнении количественных выборочных исследований статистики и аудиторы
устанавливают только один допустимый уровень значения признака. Аудиторы, в
частности, устанавливают значение существенной ошибки, превышение которой считается
не приемлемым[1].
Приемлемый риск ошибочного
принятия (ARIA – acceptable risk of incorrect acceptantace) - это статистический риск того, что
совокупность, будет принята, хотя она и содержит существенную ошибку.
Приемлемый риск ошибочного
непринятия (ARIR – acceptable risk of incorrect rejection)
- это статистический риск того, что будет сделан вывод о наличии
существенной ошибки в совокупности, хотя на самом деле ошибки нет.
При одной норме величины
ошибки риски зависят только от доверительной вероятности и определяются так:
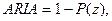
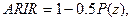
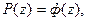
где P(z) – доверительная вероятность;
Ф(z) – функция Лапласа;
Z – коэффициент
доверительного интервала.
Эту зависимость
иллюстрирует следующие данные:
P(z), % = 99 95 90 80 70
60 50
ARIA, % = 0.5
2.5 5 10
30 40 50
ARIR, % = 1
5 10 20
15 20 25
Z = 2.58
1.96 1.64 1.28
1.15 1.04 0.84
Определение объема
выборки. Располагая некоторой информацией о изменчивости изучаемого признака
очень большой совокупности, минимальный размер выборки определяют на основе
классического метода, при котором относительную ошибку оценки признака и риск
принимают равными. Тогда для определения параметра с заданной точность
необходима выборка величиной:
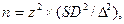
где 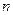 - объем выборки,
необходимый и достаточный для оценки среднего значения признака;
- объем выборки,
необходимый и достаточный для оценки среднего значения признака;
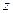 - коэффициент доверительного
интервала;
- коэффициент доверительного
интервала;
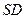 - предварительная
оценка стандартного отклонения признака;
- предварительная
оценка стандартного отклонения признака;
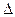 - задаваемая
требованиями исследования ошибка определения признака.
- задаваемая
требованиями исследования ошибка определения признака.
Нередко выполняются
выборочные исследования в которых оценивают многомерные случайные переменные.
Например, бывает необходимо оценивать выбор потребителей одного из нескольких
объектов, или одной из нескольких характеристик объекта. В таких случаях размер
выборки оценивается следующим образом[2]:
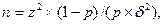
где 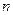 - объем выборки
необходимый и достаточный для оценки вероятности выбора с относительной
погрешностью не выше установленной;
- объем выборки
необходимый и достаточный для оценки вероятности выбора с относительной
погрешностью не выше установленной;
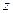 - коэффициент
доверительного интервала, соответствующий заданной погрешности;
- коэффициент
доверительного интервала, соответствующий заданной погрешности;
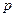 - частость выбора;
- частость выбора;
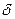 - задаваемая
относительная погрешностью
- задаваемая
относительная погрешностью
Выборки при ограниченных
размерах совокупности и различных уровнях доверия к рискам первого и второго
рода нередко используются в сфере экономического анализа, аудита и маркетинга.
Объем выборки в таком случае определяется следующим образом:
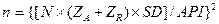 ,
,
где 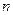 - начальный объем
выборки;
- начальный объем
выборки;
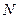 - объем совокупности;
- объем совокупности;
 - доверительный
коэффициент для ARIA;
- доверительный
коэффициент для ARIA;
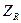 - доверительный
коэффициент для ARIR;
- доверительный
коэффициент для ARIR;
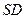 - предварительная
оценка стандартного отклонения;
- предварительная
оценка стандартного отклонения;
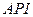 - допустимый интервал
точности;
- допустимый интервал
точности;
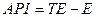 ;
;
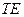 -допустимая ошибка
для совокупности;
-допустимая ошибка
для совокупности;
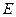 - оцененная точечная
оценка для ошибки совокупности.
- оцененная точечная
оценка для ошибки совокупности.
Пример. Требуется
установить объем выборки первичных документов из совокупности в 4000
документов, в результате учета которых сформирована статья баланса, которая
должна быть принята или отвергнута. Налоговой инспектор счел возможным
установить приемлемый риск ошибочного принятия (ARIA) на уровне доверительной вероятности
80%, а приемлемый риск ошибочного непринятия (ARIR) на уровне доверительной вероятности
75%. Допустимая ошибка для совокупности – статьи баланса – инспектор установил
в общем денежном выражении в размере ±21000 руб. Предварительная точечная
оценка ошибки совокупности – статьи баланса на основе предшествующих проверок
фирмы установлена в размере 1500 руб. Предварительная оценка стандартной ошибки
первичного документа установлена в размере 20 руб.
По вышеприведенным
формулам для ARIA при P(z)=80%  =1.28; для ARIR при P(z)=75%
=1.28; для ARIR при P(z)=75% 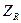 =1,15. Тогда
=1,15. Тогда 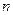 ={[4000*(1.28+1.15)*20]/(21000-1500)}
={[4000*(1.28+1.15)*20]/(21000-1500)}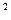 =100.
=100.
Расчетный интервал
точности при требуемом уровне доверия по итогам проведения исследования
определяется следующим образом:
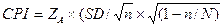 ,
,
где SD определяется по результатам
обработки данных выборки.
Расчетный верхний
доверительный интервальный предел (UCL) и расчетный нижний доверительный
предел (LCL) определяются как
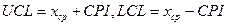 ,
,
где 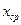 - точечная оценка среднего
значения признака совокупности.
- точечная оценка среднего
значения признака совокупности.
В результате проверки
учета по 100 первичным документам было обнаружено несколько ошибок. По
вышеприведенным формулам определены выборочная средняя ошибка и выборочное
стандартное отклонение: 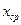 =2,26 руб. и SD=21,2 руб.
=2,26 руб. и SD=21,2 руб.
Поскольку в этом примере
инспектор оценивает величину, равную сумме всех элементов совокупности, то она
больше средней величины объекта в N раз и определяется как:
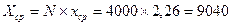 руб.
руб.
Величину расчетного
интервала при требуемом уровне доверия, подсчитываемого по формуле, необходимо
также увеличить в N раз: 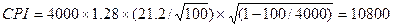 руб. Определяем по
формулам: UCL=9040+10800=19840 руб., LCL=9040-10800=-1760 руб.
руб. Определяем по
формулам: UCL=9040+10800=19840 руб., LCL=9040-10800=-1760 руб.
Полученные на основе
выборочного исследования данные о расчетных доверительных пределах интервала
точности укладываются в пределы, установленные инспектором, следовательно, по
рассматриваемой статье баланс следует принять[3].
33. Индексный
метод и его использование в
экономическом анализе
В статистике, планировании
и анализе хозяйственной деятельности основой для количественной оценки роли
отдельных факторов в динамике изменений обобщающих показателей являются
индексные модели.
Индекс – это
относительная величина, характеризующая соотношение двух значений показателя,
описывающего одно и тоже явление:
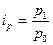 ,
,
где 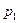 - сравниваемый
уровень;
- сравниваемый
уровень;
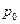 - базисный уровень.
- базисный уровень.
Подразумеваемое в индексе
сравнение обычно выполняется в одном из трех случаев: в динамике, в пространстве
(например, с эталоном, нормативом), с планом.
Индекс называется простым
(синонимы: частный, индивидуальный), если исследуемый признак берется без учета
связи его с другими признаками изучаемых явлений и сводным (синонимы: общий,
аналитический), если исследуемый признак берется не изолированно, а в связи с
другими признаками, например по нескольким логически сопрягаемым элементам.
Необходимость в расчете
сводных индексов обусловлена тем обстоятельством, что большинство экономических
явлений многоаспектны и достаточно сложны. Так, характеризуя экономическую
ситуацию, можно оценивать, например, изменения цены на какой-то отдельный,
наиболее важный товар, а можно анализировать изменение цен в среднем. Последний
случай как раз и иллюстрирует в надобности оценки соотношения некоторых
усредненных характеристик анализируемого явления: изменение цены на конкретный
вид товара описывается индивидуальным индексом цен, на всю номенклатуру товаров
или некоторую потребительскую корзину – сводным индексом цен.
Сводный индекс дает
характеристику изменения оцениваемого показателя в среднем. Поскольку
усреднения можно делать разными способами, существуют различные методы его
расчета. Тем не менее из всех форм представления сводного индекса наибольшее
распространение получило агрегатное его
представление.
Агрегатный индекс всегда
состоит из двух компонентов: индексируемого признака 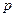 , то есть признака динамика которого исследуется, и весового признака
, то есть признака динамика которого исследуется, и весового признака 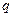 ; пример – индекс цен, при расчете которого помимо
индексируемого признака (цена) используется и весовой признак (объем проданных товаров в натуральных
измерителях). С помощью признаков весов изменяется динамика сложного
экономического явления отдельные элементы которого не соизмеримы. В
экономических исследованиях простые и агрегатные индексы дополняют друг друга.
; пример – индекс цен, при расчете которого помимо
индексируемого признака (цена) используется и весовой признак (объем проданных товаров в натуральных
измерителях). С помощью признаков весов изменяется динамика сложного
экономического явления отдельные элементы которого не соизмеримы. В
экономических исследованиях простые и агрегатные индексы дополняют друг друга.
С помощью индексного
метода в анализе решаются следующие задачи: оценка изменения уровня явления,
выявления роли отдельных факторов в изменение результативного показателя,
оценка влияния изменения структуры совокупности на динамику среднего уровня
анализируемого показателя, пересчет показателей для сравнения и др. Особенно
широкое применение эти задачи находят в факторном анализе. Логика решения
большинства из пе6речисленных задач весьма очевидна. Определенную сложность
представляет лишь задача оценки влияния изменения структуры совокупности на
динамику среднего уровня на анализируемого показателя; поэтому рассмотрим ее
подробнее.
Необходимость решения
этой задачи возникает при анализе объемных показателей (например, товарооборот
магазина зависит от многих факторов; один из них – структура товарооборота,
поскольку даже на интуитивном уровне понятно, что повышение в товарообороте
доли менее издержкоемких или более дорогих товаров безусловно влияет на его
величину) и средних уровней анализируемого показателя (например, повышение доли
рисковых ценных бумаг на рынке с очевидность приведет к повышению уровня риска
на рынке в среднем).
Для оценки степени
влияния сдвигов в структуре изучаемого явления (структура товарооборота,
состава работников, закупаемого сырья, портфеля ценных бумаг и др.). В
статистике введены понятия индексов постоянного и переменного состава.
Рассмотрим их логику на примере с индексом цен, который характеризует изменение
средней цены по выбранной номенклатуре товаров.
Среднюю цену по группе
товаров можно представить следующим образом:
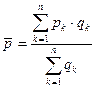 ,
,
где 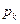 - цена
- цена 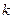 -го товара (товарной группы);
-го товара (товарной группы);
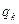 - обем продажи
- обем продажи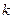 -го товара (товарной группы) в натуральных единицах;
-го товара (товарной группы) в натуральных единицах;
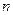 - количество товара
(товарных групп).
- количество товара
(товарных групп).
После преобразования формулы получаем
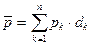 ,
,
где 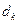 - доля
- доля 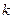 -го товара (товарной группы) в общем товарообороте.
-го товара (товарной группы) в общем товарообороте.
Из этой формулы видно,
что средняя цена зависит от двух факторов (параметров): цены 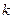 -го товара (товарной группы) и его доли в товарообороте
(последний фактор и называют структурой товарооборота), т.е. может быть
представлена функция двух параметров:
-го товара (товарной группы) и его доли в товарообороте
(последний фактор и называют структурой товарооборота), т.е. может быть
представлена функция двух параметров:
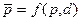 ,
,
где 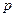 - цена;
- цена;
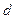 - структура товарооборота.
- структура товарооборота.
С помощью индексного
метода в рамках приведенной модели можно проанализировать, в какой степени
средняя цена за истекший период изменилась под влиянием (а) изменение цен на
отдельные товары и (б) изменение структуры товарооборота (иначе говорят:
структурных сдвигов в товарообороте).
В последующих выкладках,
чтобы не загромождать формульные представления, мы будем опускать индексы
суммирования 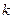 и
и 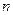 . Итак, анализируется переход в состояние средней цены в
базисном и отчетном периодах; все показатели, относящиеся к базисному
периоду, имеют индекс «0», к отчетному –
«1».
. Итак, анализируется переход в состояние средней цены в
базисном и отчетном периодах; все показатели, относящиеся к базисному
периоду, имеют индекс «0», к отчетному –
«1».
Исходя из определения
индекса цен и выполняя аналогичные выше произведенные элементарные
преобразования получим:
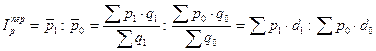 .
.
Этот индекс называется
индексом переменного состава, поскольку при его расчете меняются как цены
отдельных товаров, так и структура товарооборота – это видно из приведенной
формулы, в которой оба параметра имеют разные индексы. Таким образом, общее
изменение средней цены за истекший период включают в себя:
- изменение средней цены
за счет изменения цен отдельных товаров;
- изменение средней цены
за счет изменения структуры товарооборота:
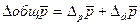 .
.
Путем несложных
преобразований формулы можно вычленить влияние каждого из приведенных факторов:
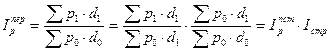 .
.
Итак, индекс переменного
состава равен произведению индекса постоянного состава и индекса структурных
сдвигов, причем первый сомножитель характеризует влияние изменения цен отдельных
товаров на изменение средней цены (влияние других факторов элиминировано), а
второй – влияние структурных сдвигов в товарообороте на изменение средней цены
по всей совокупности товаров. Поскольку в первом сомножителе фактор «структура»
не меняется, этот индекс называется индексом постоянного состава. Во втором
сомножителе обособлено влияние только изменений в структуре, поэтому данный
индекс может использоваться для анализа влияния данного фактора на изменение
результативного показателя.
В условиях модели,
связывающий товарооборот, цену и количество проданных товаров, индекс
постоянного состава в отечественной статистике традиционно носит название
индекса цен[4].
Изучая зависимость объема
выпуска продукции на предприятии от изменений численности работающих и
производительности их труда, можно воспользоваться следующей системой
взаимосвязанных индексов:
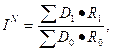 (1)
(1)
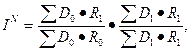 (2)
(2)
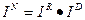 ,
(3)
,
(3)
где 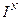 - общий индекс
изменения объема выпуска продукции;
- общий индекс
изменения объема выпуска продукции;
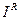 - индивидуальный (факторный) индекс изменения численности работающих;
- индивидуальный (факторный) индекс изменения численности работающих;
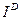 - факторный индекс
изменения производительности труда работающих;
- факторный индекс
изменения производительности труда работающих;
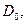
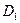 - среднегодовая
выработка товарной (валовой) продукции на одного работающего соответственно в
базисном и отчетном периодах;
- среднегодовая
выработка товарной (валовой) продукции на одного работающего соответственно в
базисном и отчетном периодах;
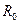 ,
, 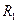 - среднегодовая
численность промышленно-производственного персонала соответственно в базисном и
отчетном периодах.
- среднегодовая
численность промышленно-производственного персонала соответственно в базисном и
отчетном периодах.
Приведенные формулы
показывают, что общее относительное изменение объема выпуска продукции
образуется как произведение относительных изменений двух факторов: численности работающих и
производительности их труда. Формулы отражают принятую в статистике практику
построения факторных индексов, суть которой можно сформулировать следующим
образом.
Если обобщающий
экономический показатель представляет собой произведение количественного
(объемного) и качественного
показателей-факторов, то при определении влияния количественного фактора
качественный показатель фиксируется на базисном уровне, а при влиянии качественного
фактора количественный показатель фиксируется на уровне отчетного периода.
Индексный метод позволяет
провести разложение по факторам не только относительных, но и абсолютных
отклонений обобщающего показателя.
Формула 1 позволяет
вычислить величину абсолютного отклонения (прироста) обобщающего показателя –
объема выпуска товарной продукции предприятия:
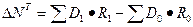 ,
,
где 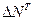 - абсолютный прирост
объема выпуска товарной продукции в анализируемом периоде.
- абсолютный прирост
объема выпуска товарной продукции в анализируемом периоде.
Это отклонение
образовалось под влиянием изменений численности работающих и производительности
их труда. Чтобы определить, какая часть общего изменения объема выпуска
продукции достигнута за счет изменения каждого из факторов в отдельности,
необходимо при расчете влияния одного из них элиминировать влияние другого
фактора.
Формула 2 соответствует
данному условию. В первом сомножителе элиминировано влияние производительности
труда, во втором – численности работающих, следовательно, прирост объема
выпуска продукции за счет изменения численности работающих определяется как
разность между числителем и знаменателем первого сомножителя:
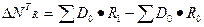 .
.
Прирост объема выпуска
продукции за счет изменения производительности труда работающих определяется
аналогично по второму сомножителю:
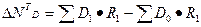 .
.
Изложенный принцип
разложения абсолютного прироста (отклонения) обобщающего показателя по факторам
пригоден для случая, когда число факторов равно двум (один из них
количественный, другой качественный), а анализируемый показатель представлен
как произведение.
Теория индексов не дает
общего метода разложения абсолютных отклонений обобщающего показателя по
факторам при числе факторов более двух[5].
Список
литературы
1. Ковалев А.И. Анализ финансового
состояния предприятия. – М.: Центр экономики и маркетинга, 2000. – с.208
2. Баканов М.И., Шеремет А.Д. Теория
экономического анализа: Учебник. – 4-е изд-е, доп. и перераб. – М. Финансы и
статистика, 1997. – с.416
3. Аренс А., Лоббек Дж. Аудит / Пер.
С англ. М.: Финансы и статистика, 1995, с. 458
4. Басовский Л.Е. Теория
экономического анализа: Учебное пособие. – М.: ИНФРА-М, 2004.-222с.
5. Шелобаев С.И. Математические
методы и модели в экономике, финансах: Учебное пособие для вузов. – М.:
ИНИТИ-ДАНА, 2000.-367с.
[1] Аренс А., Лоббек Дж. Аудит
/ Пер. С англ. М.: Финансы и статистика, 1995, с. 458
[2] Басовский
Л.Е. Теория экономического анализа: Учебное пособие. – М.: ИНФРА-М, 2004.-65с.
[3] Шелобаев С.И.
Математические методы и модели в экономике, финансах: Учебное пособие для
вузов. – М.: ИНИТИ-ДАНА, 2000.-141с.
[4] Ковалев А.И. Анализ
финансового состояния предприятия. – М.: Центр экономики и маркетинга, 2000. –
с.114
[5] Баканов М.И., Шеремет А.Д.
Теория экономического анализа: Учебник. – 4-е изд-е, доп. и перераб. – М.
Финансы и статистика, 1997. - 118