ЗАДАНИЕ 3. Рисование линий по алгоритму Брезенхема.

Основная идея алгоритма состоит в том, что если угловой коэффициент прямой < 1/2, то следующую точку поставить в позицию (1,0), а если угловой коэффициент > 1/2, то - в позицию (1,1). Для того чтобы принять решение, куда заносить очередной пиксел вводится величина отклонения D точной позиции от середины между двумя возможными растровыми точками в направлении наименьшей относительной координаты. Знак D используется как критерий для выбора ближайшей растровой точки. Если D < 0, то точное Y-значение округляется до меньшего последнего целочисленного значения Y, т.е. Y-координата не меняется по сравнению с предыдущей точкой. В противном случае Y увеличивается на 1.

Листинг программы

dx = abs(x2-x1);

dy = abs(y2-y1);

sx = x2 >= x1 ? 1:-1;

sy = y2 >= y1 ? 1:-1;

    if(dy <= dx)                     //проверка угла наклона линии

    {

 d=(dy<<1)-dx;                       //деление на два для определения углового коэффициента

 d1=dy<<1;

 d2=(dy-dx)<<1;

 Canvas->Pixels[x1][y1] = color;                   //вывод первой точки на экране

    for(int x=x1+sx, y=y1, i=1; i<=dx; i++, x+=sx) // цикл вывода линии на экран

    {

      if(d>0)            / * Если d < 0 значение y не меняется по сравнению с предыдущей точкой, иначе y увеличивается * /

      {

        d+=d2;

        y+=sy;

      }

        else d+=d1;

   Canvas->Pixels[x][y]=color;                    //вывод на экран очередной точки линии

    }

    }

    else

    {

        d=(dx<<1)-dy;

        d1=dx<<1;

        d2=(dx-dy)<<1;

        Canvas->Pixels[x1][y1] = color;

        for(int x=x1,y=y1+sy,i=1;i<=dy;i++,y+=sy)

        {

            if(d>0)

            {

                d+=d2;

                x+=sx;

            }

            else d+=d1;

            Canvas->Pixels[x][y] = color;

    }

Задание 4 Рисование блок-схемы

1.     Нарисуйте детальную блок-схему данного алгоритма и реализуйте его на языке программирования. Программа должна выводить исходный многоугольник на экран, а затем, если многоугольник не выпуклый, то при нажатии любой из клавиш он должен разбиваться на n выпуклых многоугольников и результаты разбиения должны выводиться на экран. Координаты исходного многоугольника должны содержаться в файле на диске.

2.     Выясните, будет ли работать ваша программа с многоугольником, изображенном на рисунке 3.

3.     Скорректируйте вашу программу так, чтобы она работала с любыми невыпуклыми многоугольниками.

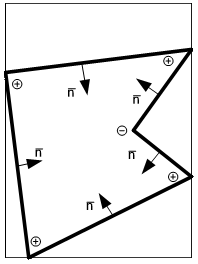
Рис. 1

Алгоритм разбиения невыпуклых многоугольников для отдельных случаев может быть представлен в следующей последовательностью:

1.     найти вогнутую вершину.

2.     соединить вогнутую вершину с предыдущей через одну.

   3.  проанализировать каждый из вновь образованных многоугольников (п.1,2,3)

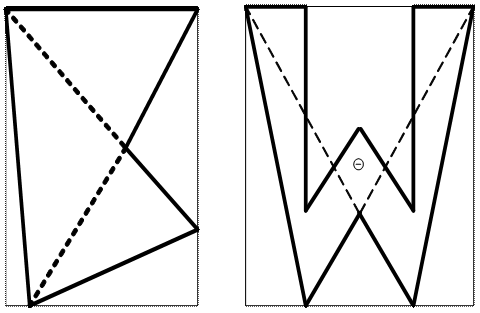
Рис. 2                           Рис. 3

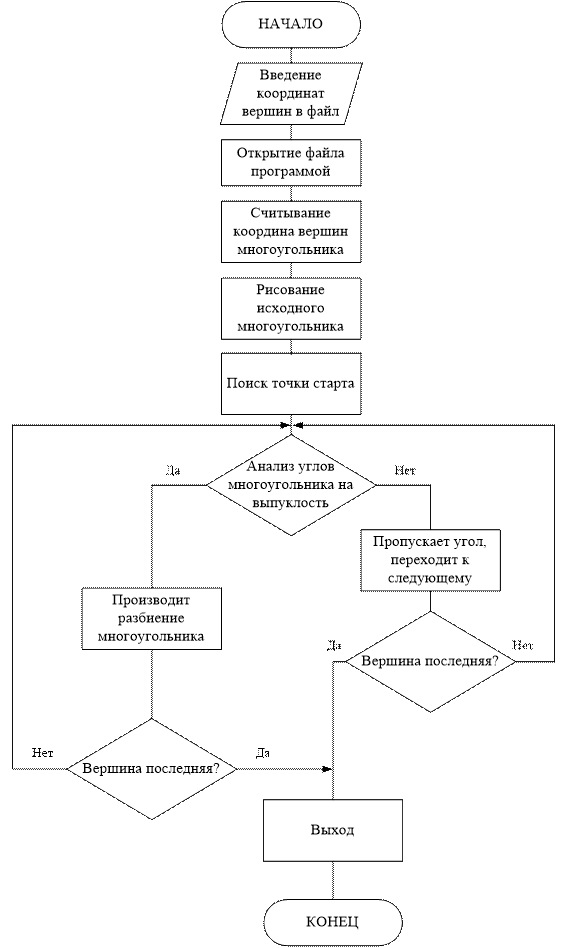
Для уменьшения размеров алгоритма  все последовательные операции были перечислены виде информационных блоков, все выражения и функции подробно указаны в листинге программы.

Данная программа выводит исходный многоугольник, взяв координаты вершин из заранее подготовленного файла, автоматически производит его анализ и построение на экране. Если многоугольник выпуклый, то его разбиения не  происходит. В противном случае, программа находит вогнутую вершину и соединяет её с предыдущей через одну. В программе исходный многоугольник отображён красным цветом, а результат его разбиения синим.

Достоинство данной программы заключается в том, что она (программа) позволяет строить многоугольники с произвольным (любым количеством) вершин.

Программа работает с различными видами многоугольников, независимо от их сложности и количества вершин.

ПОРЯДОК РАБОТЫ С ПРОГРАММОЙ

1. Для ввода исходных данных необходимо открыть текстовый файл “text” ввести построчно координаты Х , Y таким образом, чтобы координаты X ,Y одной вершины были расположены на одной строке и разделены пробелом.

2. Закрыть файл, сохранив изменения.

3. Запустить файл   Project1.ехе

4. Кликнуть два раза по открывшейся форме.

5. Во вновь появившемся меню выбрать файл “text”.

6. Нажать кнопку «ОТКРЫТЬ» и программа автоматически произведёт построение фигуры с заданными вершинами. Исходный многоугольник отображён красным цветом, а результат его разбиения синим

ЛИСТИНГ ПРОГРАММЫ РАЗБИЕНИЯ МНОГОУГОЛЬНИКОВ

unit Unit1;

interface

uses

  Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

  Dialogs, ExtCtrls;

type

  TForm1 = class(TForm)

    Image1: TImage;

    OpenDialog1: TOpenDialog;

    procedure Image1Click(Sender: TObject);

  private

    { Private declarations }

  public

    { Public declarations }

    procedure Razb(X,Y:TStringList);

  end;

  TLine = record  //для хранения уравнения линии

    K,

    B : Real;

  end;

var

  Form1: TForm1;

  X,Y:TStringList;

  function GetUrLine(sx1,sy1, sx2,sy2:String):TLine;

  function Sravnit(zUrLine:TLine; X,Y:String):Boolean;

implementation

uses StrUtils;

{$R *.dfm}

//------------------------------------------------------------------------------

//Проверяет лежит ли точка выше прямой, задоваемой уравнением

function Sravnit(zUrLine:TLine; X,Y:String):Boolean;

begin

  Result:=(zUrLine.K*StrToInt(X)+zUrLine.B)>StrToInt(Y);

end;

//------------------------------------------------------------------------------

//Возвращает уравнение прямой

function GetUrLine(sx1,sy1, sx2,sy2:String):TLine;

var x1,y1, x2,y2:Integer;

begin

  x1:=StrToInt(sx1);

  y1:=StrToInt(sy1);

  x2:=StrToInt(sx2);

  y2:=StrToInt(sy2);

  if x1=x2 then Result.K:=100000

           else Result.K:=(y2-y1)/(x2-x1);

  Result.B:=y1-Result.K*x1;

end;

//------------------------------------------------------------------------------

//Процедура разбиения многогранника на выпуклые...

procedure TForm1.Razb(X,Y:TStringList);

var i, j, k, ks, f:Integer;

    Pr, PrLine:Boolean;

    UrLine:TLine;

    X1,Y1 : TStringList;

begin

  //поиск точки старта поиска

  f:=0;

  pr:=True;

  while Pr do

  begin

    if f+1>X.Count-1 then k:=f+1-X.Count else k:=f+1;

    UrLine:=GetUrLine(X[f],Y[f], X[k],Y[k]);

    if f+2>X.Count-1 then k:=f+2-X.Count else k:=f+2;

    PrLine:=Sravnit(UrLine, X[k],Y[k]);

    ks:=0;

    for j:=2 to X.Count-1 do

    begin

      if f+j>X.Count-1 then k:=f+j-X.Count else k:=f+j;

      if PrLine=Sravnit(UrLine, X[k],Y[k]) then Inc(ks);

    end;

    pr:=not(ks=X.Count-2);

    f:=f+1;

  end;

  f:=f-1;

  //Проверяем выпуклый ли многоугольник....

  Pr:=True;

  i:=0;

  while Pr and (i<X.Count) do

  begin

    if i+1+f>X.Count-1 then k:=i+1+f-X.Count else k:=i+f+1;

    UrLine:=GetUrLine(X[i+f],Y[i+f], X[k],Y[k]);

    if i+2+f>X.Count-1 then k:=i+f+2-X.Count else k:=i+f+2;

    PrLine:=Sravnit(UrLine, X[k],Y[k]);

    ks:=0;

    for j:=2 to X.Count-1 do

    begin

      if i+f+j>X.Count-1 then k:=i+f+j-X.Count else k:=i+f+j;

      if PrLine=Sravnit(UrLine, X[k],Y[k]) then Inc(ks);

    end;

    pr:=(ks=X.Count-2);

    i:=i+1;

  end;

  if not(Pr) then  //многоугольник не выпуклый

  begin

    //Рисуем доп. линию (треугольник)

    with Image1.Canvas do

    begin

      Pen.Color:=clBlue;   //синим цветом

      Pen.Width:=3;        //толщиной 3 пикселя

      if i+f>x.Count-1 then k:=i-X.Count+f else k:=i+f;

      MoveTo(StrToInt(X[k]), StrToInt(Y[k]));

      if i-2+f<0 then k:=X.Count-2+f else k:=i-2+f;

      LineTo(StrToInt(X[k]), StrToInt(Y[k]));

    end;

    X1:=TStringList.Create;

    Y1:=TStringList.Create;

    if X.Count>4 then

    begin

      for j:=0 to X.Count-2 do

      begin

        if i+j+f>X.Count-1 then k:=i+j+f-X.Count else k:=i+f+j;

        X1.Add(X[k]);

        Y1.Add(Y[k]);

      end;

      Razb(X1,Y1);

    end;

  end;

end;

//------------------------------------------------------------------------------

//Открытие файла

procedure TForm1.Image1Click(Sender: TObject);

var zList:TStringList;

    i,j:Integer;

begin

  if OpenDialog1.Execute then

  begin

    X:=TStringList.Create;

    Y:=TStringList.Create;

    zList:=TStringList.Create;

    zList.LoadFromFile(OpenDialog1.FileName);

    for i:=0 to zList.Count-1 do

    begin

      j:=PosEx(' ',zList[i]);

      X.Add(copy(zList[i],1,j-1));

      Y.Add(copy(zList[i],j+1,length(zList[i])-j))

    end;

    //Нарисовать исходный многогранник

    with Image1.Canvas do

    begin

      Pen.Color:=clRed;    //красным цветом

      Pen.Width:=4;        //ширина линии - 4

      MoveTo(StrToInt(X[0]), StrToInt(Y[0]));

      for i:=1 to X.Count-1 do

        LineTo(StrToInt(X[i]), StrToInt(Y[i]));

      LineTo(StrToInt(X[0]), StrToInt(Y[0]));

    end;

    Razb(X,Y);           //процедура разбиения

  end;

end;

end.