Машинная графика в настоящее время уже вполне сформировалась как наука. Существует аппаратное и программное обеспечение для получения разнообразных изображений - от простых чертежей до реалистичных образов естественных объектов. Машинная графика используется почти во всех научных и инженерных дисциплинах для наглядности восприятия и передачи информации. Знание её основ в наше время необходимо любому ученому или инженеру. Машинная графика властно вторгается в бизнес, медицину, рекламу, индустрию развлечений. Примене­ние во время деловых совещаний демонстрационных слайдов, под­готовленных методами машинной графики и другими средствам автоматизации конторского труда, считается нормой. В медицине становится обычным получение трехмерных изображений внутренних ­органов по данным компьютерных томографов. В наши дни телевидение и другие рекламные предприятия часто прибегают к услугам машинной графики и компьютерной мультипликации. Использование машинной графики в индустрии развлечений охватыва­ет такие несхожие области как видеоигры и полнометражные художественные фильмы[1].

В рамках данной работы будут рассмотрены принципы создания и применения компьютерных трёхмерных изображений. Для этого приходится применять математический аппарат и техники программирования.

Задание 1. Деловая графика

Постановка задачи

Требуется составить в MS Excel электронную таблицу любых статистических данных и построить диаграмму. Тип диаграммы для 2 варианта – поверхность.

Описание метода решения

Табличный процессор MS Excel – мощное средство для работы с электронными таблицами, пригодное для применения в профессиональных и бытовых целях. В этой программе имеется большое количество средств визуализации табличной информации. Мы рассмотрим один из способов – построение поверхности. В этом случае в трёх координатах строится поверхность, которая отображает числовые данные A(i,j) в конкретной строке i и столбце j таблицы как зависимость координаты z от заданных двух (x,y), то есть

z(x,y) = F(x,y) = A(i,j)

Кроме этого, используется отображение различных диапазонов значений различными цветами. Дла расшифровки диапазонов для каждого цвета справа от изображения поверхности расположена легенда

В качестве отображаемой поверхности использована функция

F(x,y) = cos(0.2x*0.1y),

которая реализована в соттветствующей таблице, с использованием ссылок Excel на ячейки.

Excel позволяет масштабировать, поворачивать, использовать перспективу для полученных изображений. Эти параметры изменяются с помощью мышки или в диалоговоых окнах. Используя эти настройки, полученная поверхность была приведена к наиболее удобному для восприятия информации виду[2].

Вывод

Используя стандартные возможности программы Excel, можно визуализировать табличные данные, и получить красивые и наглядные графики и диаграммы. Один из видов трехмерной диаграммы – поверхность, и была построена в рамках этой работы.

Задание 2. Трёхмерные преобразования

Постановка задачи

Требуется составить программу, реализующую трёхмерные преобразования с фигурой. Для варианта 2 это перенос параллелограмма по осям X,Y,Z. Фигура должна отображаться в контурном виде без удаления невидимых линий и уметь вращаться вокруг произвольной оси. Управление должно осуществляться с помощью клавиш 1-9 на цифровой клавиатуре

Описание метода решения

В памяти компьютера хранится модель фигуры – параллелограмма, в виде 12 рёбер. Каждое ребро задано в виде 6 чисел – координат x,y,z начала и конца ребра. Координаты заданы относительно геометрического центра фигуры.

Фигура находится в глобальной трёхмерной системе координат. Оси глобальной системы координат X,Y,Z направлены соответственно вправо, вверх и вперёд относительно человека, сидящёго за монитором. Центр экрана имеет координаты (0,0,0). Также хранится значение угла альфа – угла поворота фигуры относительно вертикальной оси (Y). При угле альфа равном 2πn, где n – целое число, направлнение осей глобальной системы координат, и системы в которой задана фигура, совпадают. Таким образом, зная положение вершин фигуры в её собственной системе координат, и угол альфа, можно получить их положение в глобальной системе координат[3]:

x_г = x_ф*cos(γ) + z_ф*sin(γ) + x₀

z_г = z_ф*cos(γ) - x_ф*sin(γ) + z₀                                                                                     (1)

y_г = y_ф + y₀

где

x_г, y_г, z_г – положение точки в глобальной системе координат,

x_ф, y_ф, z_ф - положение точки в системе координат фигуры,

x₀, y₀, z₀ – положение начала координат фигуры в глобальной системе координат,

 γ – угол поворота фигуры, то есть угол между осями X глобальной системы координат и системы координат фигуры

А с помощью преобразований подобия, из глобальных координат x_г,y_г,z_г можно получить экранные координаты x_э,y_э:

x_э = k_x*x_г*(z_б/(z_г+z_б)) + 320

y_э = - k_z*y_г*(z_б/(z_г+z_б)) + 240                                                   (2)

где

x_э, y_э – положение точки на экране (экранные координаты),

k_x, k_z – коэффициенты, связывающие экранные координаты с глобальными, то есть количество экранных пикселей в одной единице в глобальных координатах,

320, 240 – экранные координаты центра экрана

z_б – база изображения, расстояние (в глобальных координатах) между глазом наблюдателя и монитором.

Знак минус перед коэффициентом k_z связан с тем, что в глобальной системе координат вертикальная ось (Y_г) направлена вверх, а в экранной – вертикальная ось (Y_э) направлена вниз

Таким образом, с помощью двух  преобразований можно отображать фигуру на экране компьютера.

Размеры фигуры выбраны такими, чтобы коэффициенты k_x и k_z были равны 1. Базовое расстояние выбрано z_б 400 точек, и сразу внесено в z₀. С учётом этого, формулы (2) несколько упрощаются:

x_э = x_г*1000/z_г + 320

y_э = - y_г*1000/z_г + 240                                                            (2’)

Задание – перенос по осям и поворот относительно оси Y таким образом реализуется изменением смещения фигуры в глобальной системе координат x₀, y₀, z₀ и угла γ. При этом на смещение фигуры наложены ограничения x_min, x_max, y_min, y_max, z_min, z_max

Алгоритм программы содержит процедуру инициализации, в которой устанавливаются значения нужных переменных, и главный цикл, в котором считываются нажатия клавиш, затем в зависимости от нажатой клавиши производится поворот или вращение фигуры (или ничего, если была нажата неверная клавиша), и отрисовка фигуры, согласно формулам (1) и (2’). Выход из бесконечного цикла происходит по нажатию главиши Esc. Перед входом в этот цикл программа переводит экран в графический режим, после выхода – возвращает обратно в текстовый.

Движение по осям X,Y,Z производится соответственно клавишами 4 и 6, 2 и 8, 1 и 9 на цифровой клавиатуре, поворот – клавишами 3 и 7.

Фигура в программе хранится в виде массива из 12 строк по 6 чисел, каждая строка хранит координаты начала и конца одного ребра в системе координат фигуры.

Листинг кода

Программа написана на языке Турбо Паскаль 7.0. Программа состоит из одного файла, кроме того, для работы требуется наличие файла egavga.bgi в каталоге, где расположен exe-файл, при запуске оного, или в каталоге d:\bp\bgi (или любом другом, указанном в тексте) при запуске программы из компилятора.

Здесь приведена главная функция, которая отрисовывает фигуру, снабженная подробными комментариями. Полный листинг доступен в приложении.

procedure DrawFigure;   {отрисовка фигуры}

var

  i: integer;                      {счётчик цикла}

  x1,y1,z1,x2,y2,z2: real;         {глобальные координаты}

  x1s,y1s,x2s,y2s: integer;        {экранные координаты}

begin

  ClearDevice;                     {очистка экрана}

  for i := 1 to figure_size do

  begin

    {преобразование координат фигуры в глобальные}

    x1 := figure[i,1]*cos(gamma) + figure[i,3]*sin(gamma) + x0;

    y1 := figure[i,2] + y0;

    z1 := figure[i,3]*cos(gamma) - figure[i,1]*sin(gamma) + z0;

    x2 := figure[i,4]*cos(gamma) + figure[i,6]*sin(gamma) + x0;

    y2 := figure[i,5] + y0;

    z2 := figure[i,6]*cos(gamma) - figure[i,4]*sin(gamma) + z0;

    {преобрзование глобальных координат в экранные}

    x1s := Round(x1*1000/z1) + 320;

    y1s := -Round(y1*1000/z1) + 240;

    x2s := Round(x2*1000/z2) + 320;

    y2s := -Round(y2*1000/z2) + 240;

    line(x1s, y1s, x2s, y2s);

  end;

end;

Вывод

Используя упрощенный вывод (только контуры, один цвет, без удаления невидимых рёбер), можно достигнуть достаточной наглядности, как это показала работа – без труда определяется движение и вращение трёхмерной фигуры.

Задание 3. Проекции

Постановка задачи

Требуется написать программу, для изображения многогранника, вращающегося вокруг оси OY. Ось вращения не должна совпадать с собственной вертикальной осью фигуры. Для варианта 2 это тетраэдр, проекция – диметрическая. Требуется реализовать алгоритм удаления невидимых линий. Все грани рисовать разными цветами.

Описание метода решения

Аналогично предыдущему заданию, в памяти компьютера хранится модель фигуры – тетраэдра, в виде набора координат. Координаты заданы относительно геометрического центра фигуры. Однако здесь, так как требуется реализовать алгоритм удаления невидимых линий, требуется хранить не отдельные рёбра фигуры, а грани целиком. Каждая грань – треугольник, хранится в виде структуры из 12 чисел с плавающей точкой – по три координаты x,y,z для вершин треугольника и три координаты вектора – нормали (то есть вектора перпендикулярного поверхности треугольника). Этот вектор используется для отбрасывания невидимых линий – если он направлен к зрителю, то грань видна, иначе – не видна.

В отличие от предыдущего задания, где трёхмерные координаты преобразуются в двухмерные с перспективой, здесь указан тип проекции – диметрия. Такая проекция имеет два масштаба: оси X и Y с из глобальной системы координат переходят в экранную с масштабом 1:1, а ось Z переходит в наклонную прямую, располагающуюся под углом 45 с масштабом 0,5:1. Название «диметрия» как раз и обозначает «два масштаба». Заметим сразу, что положительное направление глобальной координаты Z_г отображается на экранные координаты X _э и Y _э (рис. 1) с масштабом 0,5*cos 45˚ = 0,5*0,707[4].

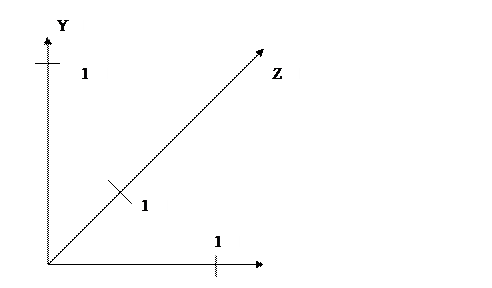
Рис. 1. Диметрическая проекция.

Формулы преобразования координат из системы координат фигуры в глобальную систему координат совпадают с приведёнными в задании 2:

x_г = x_ф*cos(γ) + z_ф*sin(γ) + x₀

z_г = z_ф*cos(γ) - x_ф*sin(γ) + z₀                                                                                     (1)

y_г = y_ф + y₀

А формулы преобразования глобальных координат в экранные отличаются:

x_э = x_г + z_г * 0,707/2 + 320

y_э = - y_г + z_г * 0,707/2 + 240                                                   (2’’)

Для определения координат нормального к поверхности вектора используем векторное произведение[5]:

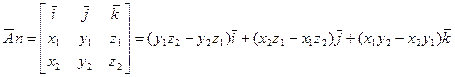     (3)

А для определения угла между двумя векторами используется скалярное произведение:

A = x_nx_v+y_ny_v+z_nz_v                                                                   (4)

где

x_n,y_n,z_n – координаты нормального вектора, а

x_n,y_n,z_n – координаты направления взгляда при диметрической поверхности, они равны (-1, -1, 2)

При этом, если угол между векторами меньше 90˚, то скалярное произведение больше нуля, а если угол больше, то скалярное произведение отрицательно. Таким образом, используя формулу (3), программа для каждой грани может посчитать нормальный вектор, а используя формулу (4), узнать, видима ли эта грань в данный момент

Листинг кода

Здесь также приведена функция отрисовки фигуры, в которой используются формулы (2’’) и (4)

procedure DrawFigure;  {отрисовка фигуры}

var

  i: integer;                                {счётчик цикла}

  x1,y1,z1,x2,y2,z2,x3,y3,z3,xn,yn,zn: real; {координаты вершин грани и нормали}

  x1s,y1s,x2s,y2s,x3s,y3s,xcs,ycs: integer;  {координаты на экране}

begin

  ClearDevice;        {очистка экрана}

  SetColor(15);       {белый цвет}

  line(100,380,540,380);      {рисуем оси координат}

  line(100,380,100,100);

  line(100,380,380,100);

  for i := 1 to figure_size do   {для каждой грани}

  begin

    {находим глобальные координаты нормали}

    xn := figure[i].xn*cos(alpha) + figure[i].zn*sin(alpha);

    yn := figure[i].yn;

    zn := figure[i].zn*cos(alpha) - figure[i].xn*sin(alpha);

    if xv*xn+yv*yn+zv*zn > 0 then    {с помощью скалярного произведения}

    begin                            {проверяем видимость грани}

      {находим глобальные координаты вершин треугольника грани}

      x1 := figure[i].x1*cos(alpha) + figure[i].z1*sin(alpha) + x0;

      y1 := figure[i].y1 + y0;

      z1 := figure[i].z1*cos(alpha) - figure[i].x1*sin(alpha) + z0;

      x2 := figure[i].x2*cos(alpha) + figure[i].z2*sin(alpha) + x0;

      y2 := figure[i].y2 + y0;

      z2 := figure[i].z2*cos(alpha) - figure[i].x2*sin(alpha) + z0;

      x3 := figure[i].x3*cos(alpha) + figure[i].z3*sin(alpha) + x0;

      y3 := figure[i].y3 + y0;

      z3 := figure[i].z3*cos(alpha) - figure[i].x3*sin(alpha) + z0;

      {пересчитываем глобальные координаты вершин треугольника в экранные}

      x1s := Round(x1+z1*0.707/2) + 320;

      x2s := Round(x2+z2*0.707/2) + 320;

      x3s := Round(x3+z3*0.707/2) + 320;

      y1s := -Round(y1+z1*0.707/2) + 240;

      y2s := -Round(y2+z2*0.707/2) + 240;

      y3s := -Round(y3+z3*0.707/2) + 240;

      {находим экранные координаты центра треугольника (для заливки)}

      xcs := Round((x1s+x2s+x3s)/3);

      ycs := Round((y1s+y2s+y3s)/3);

      {установка цвета треугольника}

      SetColor(figure[i].color);

      {отрисовка сторон треугольника}

      line(x1s, y1s, x2s, y2s);

      line(x2s, y2s, x3s, y3s);

      line(x3s, y3s, x1s, y1s);

      {установка цвета заливки}

      SetFillStyle(1,figure[i].color);

      {заливка треугольника}

      FloodFill(xcs,ycs,figure[i].color);

    end;

  end;

end;

Вывод

Используя общедоступные формулы из высшей математики и основные навыки программирования, можно составить программу, реализующую основы трёхмерной графики – определённые проекции, поворот фигуры, отсечение невидимых граней. Используя более сложны модели, можно получить изображения, близкие по качеству к профессиональным.

Заключение

Использование компьютерной графики даёт возможность облегчить труд инженера, дизайнера, проектировщика. Если раньше для подобной работы нужно было располагать мощными и сверхмощными вычислительными машинами, то сейчас такая работа по силам обычной офисной или домашней ЭВМ. Выполняя эту работу, мы на практике использовали принципы построения трехмерных изображений

Список использованной литературы

1.     Вайсберг А. В., Гриценко М. Е. Формирование структуры станка на ранних стадиях проектирования. – Точность автоматизированных производств (ТАП – 97). Сборник статей международной научно-технической конференции. Пенза, 1997.

2.     Матюшок В.М. Excel 7.0: Общие и экономические расчёты. 1997.

3.     Роджерс Д. «Алгоритмические основы машинной графики» Москва «Мир» 1989.

4.     Рябушко С.А. Сборник задач по высшей математике. М, «Высшая школа», 1998.

5.     Шикин Е. В., Боресков А. В., Зайцев А. А. «Начала компьютерной графики» Москва «Диалог - МИФИ» 1993.

[1] Д. Роджерс «Алгоритмические основы машинной графики» Москва «Мир» 1989, с. 11

[2] Excel 7.0: Общие и экономические расчёты. Матюшок В.М. 1997 с. 54, 72-77

[3] Е. В. Шикин, А. В. Боресков, А. А. Зайцев «Начала компьютерной графики» Москва «Диалог - МИФИ» 1993, с. 51

[4] Инженерная и компьютерная графика Миронов Б.Г., Миронова Р.С., Пяткина Д.А. и др. 2004. с. 35,38

[5] Рябушко С.А. Сборник задач по высшей математике. М, «Высшая школа», 1998. с. 122