ВСЕРОССИЙСКИЙ
ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА
СТАТИСТИКИ
О
Т Ч Е Т
о результатах выполнения
компьютерной лабораторной работы №1
«Автоматизированный априорный анализ
статистической совокупности
в среде MS Excel»
Вариант №18
Выполнил: ст. III
курса гр.357
Гришина
Наталья Николаевна
Проверил: профессор
Каманина Анна Михайловна
Москва,
2006 г.
Постановка задачи
При
проведении статистического наблюдения за деятельностью предприятий корпорации
получены выборочные данные по 32-м предприятиям, выпускающим однородную
продукцию (выборка 10%-ная,
механическая), о среднегодовой стоимости основных производственных фондов
и о выпуске продукции за год.
В
проводимом статистическом исследовании обследованные предприятия выступают как
единицы выборочной совокупности, а показатели Среднегодовая стоимость основных производственных фондов и Выпуск продукции – как изучаемые
признаки единиц.
|
|
|
Таблица
1
|
|
|
Исходные
данные
|
|
|
Номер
предприятия
|
Среднегодовая
стоимость основных производственных фондов, млн.руб.
|
Выпуск
продукции, млн. руб.
|
|
1
|
1070,00
|
1030,00
|
|
2
|
1260,00
|
1130,00
|
|
3
|
1300,00
|
1260,00
|
|
4
|
1370,00
|
1400,00
|
|
5
|
890,00
|
700,00
|
|
6
|
1440,00
|
1200,00
|
|
7
|
1480,00
|
1620,00
|
|
8
|
1110,00
|
1100,00
|
|
9
|
1360,00
|
1290,00
|
|
10
|
1570,00
|
1610,00
|
|
12
|
1720,00
|
1700,00
|
|
13
|
1310,00
|
1340,00
|
|
14
|
1440,00
|
1460,00
|
|
15
|
1650,00
|
1770,00
|
|
16
|
1890,00
|
1900,00
|
|
17
|
1410,00
|
1280,00
|
|
18
|
1560,00
|
1520,00
|
|
19
|
1240,00
|
950,00
|
|
20
|
1580,00
|
1300,00
|
|
21
|
1760,00
|
1750,00
|
|
22
|
1210,00
|
990,00
|
|
23
|
960,00
|
930,00
|
|
24
|
1610,00
|
1490,00
|
|
25
|
1440,00
|
1300,00
|
|
26
|
1340,00
|
1230,00
|
|
27
|
1040,00
|
800,00
|
|
28
|
1400,00
|
1250,00
|
|
29
|
1620,00
|
1370,00
|
|
31
|
1540,00
|
1300,00
|
|
32
|
1130,00
|
1160,00
|
В
процессе исследования совокупности необходимо решить ряд статистических задач
для выборочной
и генеральной совокупностей.
Статистический анализ выборочной совокупности
1. Выявить наличие среди
исходных данных резко выделяющихся значений признаков («выбросов» данных) с
целью исключения из выборки аномальных единиц наблюдения.
2. Рассчитать обобщающие
статистические показатели совокупности по изучаемым признакам: среднюю
арифметическую (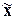 ), моду (Мо), медиану
(Ме), размах вариации (R), дисперсию(
), моду (Мо), медиану
(Ме), размах вариации (R), дисперсию( ), средние отклонения – линейное (
), средние отклонения – линейное (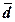 ) и квадратическое (σn),
коэффициент вариации (Vσ),
структурный коэффициент асимметрии
К.Пирсона (Asп).
) и квадратическое (σn),
коэффициент вариации (Vσ),
структурный коэффициент асимметрии
К.Пирсона (Asп).
3. На основе рассчитанных
показателей в предположении, что распределения единиц по обоим признакам близки
к нормальному, оценить:
а) степень
колеблемости значений признаков в совокупности;
б) степень
однородности совокупности по изучаемым признакам;
в)
устойчивость индивидуальных значений признаков;
г) количество
попаданий индивидуальных значений признаков в диапазоны (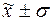 ), (
), (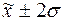 ), (
), (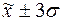 ).
).
4. Дать сравнительную
характеристику распределений единиц совокупности по двум изучаемым признакам на
основе анализа:
а) вариации
признаков;
б)
количественной однородности единиц;
в) надежности
(типичности) средних значений признаков;
г) симметричности
распределений в центральной части ряда.
5. Построить интервальный
вариационный ряд и гистограмму распределения единиц совокупности по признаку Среднегодовая стоимость основных
производственных фондов и установить характер (тип) этого распределения.
Рассчитать моду Мо полученного
интервального ряда и сравнить ее с показателем Мо несгруппированного ряда данных.
Статистический анализ генеральной
совокупности
1.
Рассчитать генеральную дисперсию 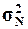 , генеральное среднее
квадратическое отклонение
, генеральное среднее
квадратическое отклонение 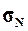 и ожидаемый размах вариации признаков RN. Сопоставить значения этих
показателей для генеральной и выборочной дисперсий.
и ожидаемый размах вариации признаков RN. Сопоставить значения этих
показателей для генеральной и выборочной дисперсий.
2.
Для изучаемых признаков рассчитать:
а) среднюю
ошибку выборки;
б) предельные ошибки выборки
для уровней надежности P=0,683, P=0,954, P=0,997 и границы, в которых будут
находиться средние значения признака генеральной совокупности при заданных
уровнях надежности.
3.
Рассчитать коэффициенты асимметрии As
и эксцесса Ek. На основе полученных
оценок сделать вывод о степени близости
распределения единиц генеральной совокупности к нормальному распределению.
Рабочий файл
|
|
|
Таблица
2
|
|
|
Аномальные
единицы наблюдения
|
|
|
Номер
предприятия
|
Среднегодовая
стоимость основных производственных фондов, млн.руб.
|
Выпуск
продукции, млн. руб.
|
|
|
11
|
590,00
|
1500,00
|
|
|
30
|
1890,00
|
500,00
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица
3
|
|
Описательные
статистики
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
|
Среднее
|
1390
|
Среднее
|
1304,333333
|
|
Стандартная
ошибка
|
44,16010578
|
Стандартная
ошибка
|
52,67921428
|
|
Медиана
|
1405
|
Медиана
|
1295
|
|
Мода
|
1440
|
Мода
|
1300
|
|
Стандартное
отклонение
|
241,8748608
|
Стандартное
отклонение
|
288,5359397
|
|
Дисперсия
выборки
|
58503,44828
|
Дисперсия
выборки
|
83252,98851
|
|
Эксцесс
|
-0,344943844
|
Эксцесс
|
-0,205332365
|
|
Асимметричность
|
-0,152503649
|
Асимметричность
|
0,042954448
|
|
Интервал
|
1000
|
Интервал
|
1200
|
|
Минимум
|
890
|
Минимум
|
700
|
|
Максимум
|
1890
|
Максимум
|
1900
|
|
Сумма
|
41700
|
Сумма
|
39130
|
|
Счет
|
30
|
Счет
|
30
|
|
Уровень
надежности(95,4%)
|
92,06551702
|
Уровень
надежности(95,4%)
|
109,8262564
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4а
|
|
Предельные
ошибки выборки
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
|
Уровень
надежности(68,3%)
|
44,96406111
|
Уровень
надежности(68,3%)
|
53,63826395
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4б
|
|
Предельные
ошибки выборки
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
|
Уровень
надежности(99,7%)
|
143,0523283
|
Уровень
надежности(99,7%)
|
170,6491441
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 5
|
|
|
Выборочные показатели вариации и асимметрии
|
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Стандартное
отклонение
|
241,8748608
|
Стандартное
отклонение
|
288,5359397
|
|
Дисперсия
|
56553,33333
|
Дисперсия
|
80477,88889
|
|
Среднее
линейное отклонение
|
191,3333333
|
Среднее
линейное отклонение
|
218,5333333
|
|
Коэффициент
вариации, %
|
17,40106912
|
Коэффициент
вариации, %
|
22,1213345
|
|
Коэффициент
асимметрии Asп
|
-0,206718465
|
Коэффициент
асимметрии Asп
|
0,015018349
|
|
|
|
|
|
|
|
Таблица
6
|
|
|
|
Карман
|
Частота
|
|
|
|
|
1
|
|
|
|
1090
|
3
|
|
|
|
1290
|
5
|
|
|
|
1490
|
11
|
|
|
|
1690
|
7
|
|
|
|
1890
|
3
|
Таблица
7
|
|
|
Интервальный
ряд распределения предприятий
по стоимости основных производственных
фондов
|
|
|
Группы
предприятий по стоимости основных фондов
|
Число
предприятий в греппе
|
Накопленная
часть группы
|
|
|
890-1090
|
4
|
13,33%
|
|
|
1090-1290
|
5
|
30,00%
|
|
|
1290-1490
|
11
|
66,67%
|
|
|
1490-1690
|
7
|
90,00%
|
|
|
1690-1890
|
3
|
100,00%
|
|
|
|
|
|
|
|
Итого
|
30
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Статистический анализ выборочной совокупности
1.Количество аномальный единиц
наблюдения – 2, согласно таблице №2: предприятие №11 со среднегодовой стоимостью
основных производственных фондов – 590 млн.руб и выпуском продукции – 1500
млн.руб., и предприятие №30 со среднегодовой стоимостью основных фондов - 1890
млн.руб. и выпуском продукции – 500 млн.руб.
2.Рассчитанные выборочные показатели
представлены в таблицах №3 и №5. Сформируем на основе этих, данных сформируем таблицу значений выборочных
показателей:
|
|
|
|
Таблица
8
|
|
Описательные
статистики выборочной совокупности
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
|
Средне
арифметическая
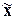
|
1040
|
Средне
арифметическая
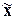
|
978,25
|
|
Медиану Ме
|
1051,25
|
Медиану Ме
|
971,25
|
|
Мода
Мо
|
1077,5
|
Мода
Мо
|
975
|
|
Размах
вариации R
|
750
|
Размах
вариации R
|
900
|
|
Средне
квадратическое отклонение σn
|
178,3570856
|
Средне
квадратическое отклонение σn
|
212,7646881
|
|
Дисперсия

|
31811,25
|
Дисперсия

|
45268,8125
|
|
Средне
линейное отклонение 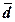
|
143,5
|
Средне
линейное отклонение 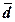
|
163,9
|
|
Коэффициент
вариации Vσ в %
|
17,14971977
|
Коэффициент
вариации Vσ в %
|
21,74952089
|
|
Коэффициент
асимметрии Asп
|
-0,21025237
|
Коэффициент
асимметрии Asп
|
0,015275091
|
3. На основе рассчитанных показателей
в предположении, что распределения единиц по обоим признакам близки к
нормальному, оценить:
а) степень колеблемости значений
признаков в совокупности. В изучаемой совокупности коэффициент вариации для
признака «Среднегодовая
стоимость основных производственных фондов» Vσ-
17,14971977%, а для признака «Выпуск продукции» Vσ- 21,74952089%. Так как
для обоих признаков коэффициент вариации меньше 40%, то степень
колеблемости значений признаков в
изучаемой совокупности незначительная;
б) степень однородности
совокупности по изучаемым признакам. Для нормальных и близких к нормальному
распределений показателей Vσ служит
индикатором однородности совокупности.
Изучаемая совокупность является количественно однородной по обоим признакам,
так как для них выполняется условие Vσ 33% (для признака «Среднегодовая стоимость основных фондов» Vσ- 17,14971977%, а для признака Vσ-21,74952089%).
в) устойчивость
индивидуальных значений признаков. Мы сопоставляем средние отклонения –
линейное 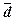 квадратическое σn . Для признака «Среднегодовая
стоимость основных фондов» отношение
квадратическое σn . Для признака «Среднегодовая
стоимость основных фондов» отношение 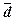 / σ равно 0,804565737,
по этому, так как не выполняется условие
устойчивости данных
/ σ равно 0,804565737,
по этому, так как не выполняется условие
устойчивости данных 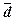 / σ£0,8, то делаем вывод, что значение данного признака не устойчивы в них имеются
«аномальные» выбросы. Поэтому, не смотря на визуальное обнаружение и исключение
нетипичных единиц наблюдения, некоторые аномалии в первичных данных продолжают
сохраняться. Выявим их путем поиска значений, выходящих из границы (
/ σ£0,8, то делаем вывод, что значение данного признака не устойчивы в них имеются
«аномальные» выбросы. Поэтому, не смотря на визуальное обнаружение и исключение
нетипичных единиц наблюдения, некоторые аномалии в первичных данных продолжают
сохраняться. Выявим их путем поиска значений, выходящих из границы (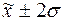 ) в качестве возможных «кандидатов» на исключение из выборки
следует рассматривать предприятие №8 (среднегодовая стоимость основных
производственных фондов равна 830 млн.руб.) и предприятие №18 (среднегодовая
стоимость основных производственных фондов равна 1167,5 млн.руд.)
) в качестве возможных «кандидатов» на исключение из выборки
следует рассматривать предприятие №8 (среднегодовая стоимость основных
производственных фондов равна 830 млн.руб.) и предприятие №18 (среднегодовая
стоимость основных производственных фондов равна 1167,5 млн.руд.)
Для признака «Выпуск продукции» отношение 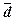 / σ равно 0,770334596, следовательно, так
как выполняется условие устойчивости данных делаем вывод об устойчивости
индивидуальных значениях признака «Выпуск продукции», т.е. об отсутствии среди
них «аномальных» вариантов значений.
/ σ равно 0,770334596, следовательно, так
как выполняется условие устойчивости данных делаем вывод об устойчивости
индивидуальных значениях признака «Выпуск продукции», т.е. об отсутствии среди
них «аномальных» вариантов значений.
г) количество попаданий индивидуальных значений
признаков в диапазоны (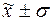 ), (
), (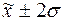 ), (
), (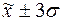 ). Сформируем следующую таблицу:
). Сформируем следующую таблицу:
Распределение значений признака по диапазонам
рассеяния признака относительно 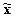
|
|
Границы диапазонов
|
Количество значений хi,, находящихся
в диапазоне
|
|
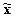 -σn£хi£ -σn£хi£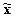 + σn + σn
|
841,6429144£хi £1218,357086
|
21
|
|
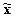 -2σn£хi£ -2σn£хi£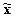 + 2σn + 2σn
|
683,2858288£хi £1396,714171
|
28
|
|
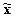 -3σn£хi£ -3σn£хi£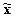 + 3σn + 3σn
|
504,9287432£хi £1575,071257
|
30
|
В нормально распределенных и
близких к нам рядах вероятностные оценки диапазонов рассеяния значений признака
таковы:
68,3% войти в диапазон (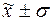 )
)
95,4% попадет в диапазон (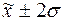 )
)
99,7% появится в диапазоне (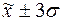 )
)
В изучаемой совокупности для признака
«Среднегодовая стоимость основных производственных фондов» процентное
соотношение рассеяния значений признака по трем диапазонам таково:
70% войти в диапазон (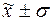 )
)
93,3% попадет в диапазон (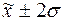 )
)
100% появится в диапазоне (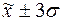 )
)
Вывод: распределение данных по
диапазонам близко к нормальному.
4. Дадим сравнительную характеристику распределений единиц
совокупности по двум изучаемым признакам на основе анализа:
а) вариации признаков. Сравним
коэффициенты вариации для изучаемых признаков: так как коэффициент вариации
доля признака «среднегодовая стоимость основных производственных фондов»,
равный 17,14971977%, меньше чем коэффициент вариации для
признака «Выпуск продукции», равный 21,74952089% то колеблемость значений
единиц совокупности для первого признака приблизительно на 1/4
меньше, чем для второго;
б) количественной однородности
единиц. По признаку «Среднегодовая стоимость основных производственных фондов
совокупность является несколько более количественно однородной, чем по признаку
«Выпуск продукции» (Vσ1< Vσ2£33%); однако, для обо из признаков достаточно
длины «хвосты», поскольку более 5% вариантов лежат за пределами интервала 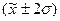 : в изучаемой совокупности -6,7% вариантов.
: в изучаемой совокупности -6,7% вариантов.
в) надежность (типичность) средних
значений признаков. Для оценки надежности (типичности) средней величины 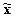 можно воспользоваться
значением показателя вариации Vσ. Так как
для признака «Среднегодовая стоимость основных производственных фондов»
коэффициент вариации Vσ = 17,14971977%
меньше, чем коэффициент вариации для
признака «Выпуск продукции» Vσ = 21,74952089%,
то средняя арифметическая величина для первого признака являемся более надежной
характеристикой, чем средняя арифметическая величина для второго признака.
можно воспользоваться
значением показателя вариации Vσ. Так как
для признака «Среднегодовая стоимость основных производственных фондов»
коэффициент вариации Vσ = 17,14971977%
меньше, чем коэффициент вариации для
признака «Выпуск продукции» Vσ = 21,74952089%,
то средняя арифметическая величина для первого признака являемся более надежной
характеристикой, чем средняя арифметическая величина для второго признака.
г) симметричности распределений в
центральной части ряда. Для оценки ассиметричности распределения в центральном
диапазоне 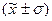 служит коэффициент К. Пирсона. В
изучаемой совокупности: для признака «Среднегодовая стоимость основны
производственных фондов» Asп=0,21025237, следовательно, имеет место левосторонняя
ассиметрия, так как Asп<0; для признака
«Выпуск продукции» Asп=0,015275091, то есть имеет место правосторонняя
ассиметрия, так как Asп<0. В обоих случаях
ассиметрия является незначительной (|Asп |£0,25), однако для признака «Выпуск продукции»
вариационный ряд более симметричен, чем для признака «Среднегодовая стоимость
основных производственных фондов».
служит коэффициент К. Пирсона. В
изучаемой совокупности: для признака «Среднегодовая стоимость основны
производственных фондов» Asп=0,21025237, следовательно, имеет место левосторонняя
ассиметрия, так как Asп<0; для признака
«Выпуск продукции» Asп=0,015275091, то есть имеет место правосторонняя
ассиметрия, так как Asп<0. В обоих случаях
ассиметрия является незначительной (|Asп |£0,25), однако для признака «Выпуск продукции»
вариационный ряд более симметричен, чем для признака «Среднегодовая стоимость
основных производственных фондов».
5.
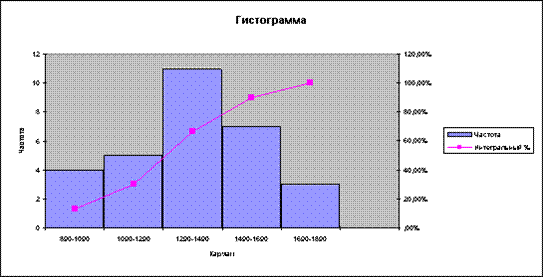
Интервальный вариационный ряд представлен в таблице 7, гистограмма
распределения единиц совокупности по признаку «Среднегодовая стоимость основных
производственных фондов»- на рисунке 1.
В исследуемой
совокупности гистограмма распределения предприятий по стоимости основных
производственных фондов имеет одновершинную форму (рс.1), поэтому есть
основания предполагать, что выборка является однородной по данному признаку.
Однако имеет место незначительная левосторонняя ассиметрия (Asп=0,21025237) и
появление 6,7% значений за пределами диапазона (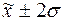 ).
).
На основе
анализа можно предположить, что распределение единиц выборочной совокупности
близко к нормальному.
Для полученного интервального ряда
значение моды Мо равно:
Мо = хмо+h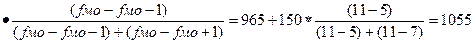
а не
сгруппированного ряда данных (по данным таблицы 3) Мо=1077,5. Данное
расхождение объясняется тем, что значение моды в таблице 3 рассчитывалось по
фактическим значениям, а для интервального ряда – по серединным.
Статистический анализ генеральной
совокупности
1. На основании таб.3 сформирует табл.10 для генеральных показателей
совокупности:
Таблица 10
Описательные
статистики генеральной совокупности
|
По столбцу «Среднегодовая стоимость основных
производственных фондов, млн.руб.»
|
По столбцу
«Выпуск продукции, млн.руб.»
|
|
Средне
квадратическое отклонение σn
|
181,4061456
|
Средне
квадратическое отклонение σn
|
216,4019548
|
|
Дисперсия

|
32908,18966
|
Дисперсия

|
46829,80603
|
|
Коэффициент
вариации Vσ в
%
|
-0,344943844
|
Коэффициент
вариации Vσ в
%
|
-0,205332365
|
|
Коэффициент
асимметрии Asп
|
0,21025237
|
Коэффициент
асимметрии Asп
|
0,015275091
|
Степень расхождения между 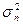 и
и 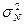 можно установить
по формуле:
можно установить
по формуле:
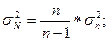
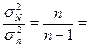 1,034482
1,034482
Прогнозные оценки размаха вариации 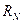 рассчитаем по формуле:
рассчитаем по формуле:
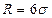
Для признака «Среднегодовая стоимость
производственных фондов» 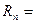 1070, в то время
как
1070, в то время
как 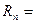 750 , т.е.
прогнозная оценка размаха вариации больше полученного размаха вариации в выборки на 320.
750 , т.е.
прогнозная оценка размаха вариации больше полученного размаха вариации в выборки на 320.
Для признака «Выпуск
продукции» 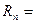 1276 , тогда как
1276 , тогда как 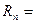 900, то есть прогнозная оценка размаха вариации больше
полученного размаха вариации в выборке 376.
900, то есть прогнозная оценка размаха вариации больше
полученного размаха вариации в выборке 376.
2. Для изучаемых признаков:
а) средняя ошибка выборки для признака
«Среднегодовая стоимость производственных фондов» равна 33,12007934, а для
признака «Выпуск продукции» - 39,50941071
б) На основании таблиц 3,4а,4б сформируем
таблицу 11.
Таблица
11
Предельные ошибки выборки и ожидаемые
границы для генеральных средних
|
Доверительная
вероятность Р
|
Коэф-фици-ент
дове-рия
t
|
Предельные
ошибки выборки
|
Ожидаемые
границы для средних 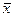
|
|
для
первого признака
|
для
второго
признака
|
для
первого признака
|
для
второго
признака
|
|
0,683
|
1
|
33,72304583
|
40,22869797
|
1006,27695£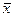 £1073,7230 £1073,7230
|
938,021302£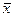 £1018,47869 £1018,47869
|
|
0,954
|
2
|
69,04913776
|
82,3696922
|
970,95086£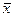 £1109,0491 £1109,0491
|
895,8803078£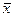 £1060,61969 £1060,61969
|
|
0,997
|
3
|
107,2892462
|
127,9868581
|
932,71075£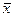 £1147,289 £1147,289
|
850,2631419£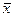 £1106,23685 £1106,23685
|
3. В изучаемой совокупности
распределения единиц выборочной совокупности по исследуемым признакам близко к
нормальному; выборка считается репрезентативной (значения показателей 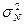 и
и
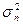 расходятся не значительно); при этом
коэффициенты Asп для обоих признаков указывают на незначительную величину ассиметрии
(для признака «Среднегодовая стоимость основных фондов»
расходятся не значительно); при этом
коэффициенты Asп для обоих признаков указывают на незначительную величину ассиметрии
(для признака «Среднегодовая стоимость основных фондов» 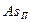 =0,21025237; для
признака «Выпуск продукции»
=0,21025237; для
признака «Выпуск продукции» 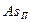 =0,01527509);
коэффициенты эксцесса для обоих признаков
=0,01527509);
коэффициенты эксцесса для обоих признаков 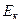 <0, т.е.
вершины кривых расположений лежат ниже вершин нормальной кривой, для признака
«Среднегодовая стоимость основных фондов»
<0, т.е.
вершины кривых расположений лежат ниже вершин нормальной кривой, для признака
«Среднегодовая стоимость основных фондов» 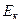 = -0,344943844, а
для признака
= -0,344943844, а
для признака
«Выпуск продукции» 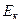 =-0,205332365,
а также небольшие абсолютные величины [
=-0,205332365,
а также небольшие абсолютные величины [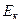 ] указывают
на незначительные отклонение эмпирического распределения от нормального. На
основе этого есть основание полагать, что распределение единиц генеральной
совокупности по изучаемым признакам будет близко к нормальному.
] указывают
на незначительные отклонение эмпирического распределения от нормального. На
основе этого есть основание полагать, что распределение единиц генеральной
совокупности по изучаемым признакам будет близко к нормальному.
Экономическая интерпретация результатов статистического
исследования предприятий
1.
Типичны ли образующие выборку предприятия по значениям изучаемых экономических
показателей?
В
результате визуального анализа диаграммы рассеяния значений показателей, были
выбраны 2 предприятий с резко выделяющимися характеристиками (см. табл.2: №11
(440;1125) и №30 (1415;375)). Они были исключены из проводимого статистического
исследования вследствие нетипичности (аномальности) этих предприятий для
изучаемой совокупности. Остальные, образующие выборку предприятий, типичны по
значениям изучаемых экономических показателей.
2.
каковы наиболее характерные для предприятий значения показателей среднегодовой
стоимости основных фондов и выпуска продукции?
Типичный уровень для предприятий
среднегодовой стоимости основных фондов – 1040 млн.руб., а типичный уровень
выпуска продукции -978,25 млн.руб.
Для признака «Среднегодовая стоимость основных
фондов» диапазон 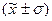 , включающие предприятия с наиболее характерными
значениями показателей следующий: (841,6429144; 1218,357086), 20 предприятий
вошедшие в этот диапазон: №2 – 942,5 млн.руб., №3 – 972,5 млн.руб., №4 – 1025 млн.руб., №6 – 1077,5 млн.руб., №7
– 1107,5 млн.руб., №9 – 1017,5 млн.руб., №10 – 1175 млн.руб., №13 – 980
млн.руб., №14 – 1077,5 млн.руб., №17 – 1055 млн.руб., №18 – 1167,5 млн.руб.,
№19 – 927,5 млн.руб., № 20 – 1182,5 млн.руб., №22- 717,5 млн.руб., №24 -1205 млн.руб.,
№25 – 1077,5 млн.руб., №26 – 1002,5 млн.руб.,
№28 – 1047,5 млн.руб., №29 – 1212,5 млн.руб., №31 – 1152,5 млн.руб., №32
– 845 млн.руб.
, включающие предприятия с наиболее характерными
значениями показателей следующий: (841,6429144; 1218,357086), 20 предприятий
вошедшие в этот диапазон: №2 – 942,5 млн.руб., №3 – 972,5 млн.руб., №4 – 1025 млн.руб., №6 – 1077,5 млн.руб., №7
– 1107,5 млн.руб., №9 – 1017,5 млн.руб., №10 – 1175 млн.руб., №13 – 980
млн.руб., №14 – 1077,5 млн.руб., №17 – 1055 млн.руб., №18 – 1167,5 млн.руб.,
№19 – 927,5 млн.руб., № 20 – 1182,5 млн.руб., №22- 717,5 млн.руб., №24 -1205 млн.руб.,
№25 – 1077,5 млн.руб., №26 – 1002,5 млн.руб.,
№28 – 1047,5 млн.руб., №29 – 1212,5 млн.руб., №31 – 1152,5 млн.руб., №32
– 845 млн.руб.
Для признака «Выпуск продукции» диапазона 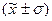 , включающий предприятия
с наиболее характерными значениями показателей следующий: (765,4853119;
1191,014688) 19 предприятие, вошедшие в этот диапазон, следующие: №1 – 772,5
млн.руб., №2 – 847,5 млн.руб., №3 – 945 млн.руб., №4 – 1050 млн.руб., №6 – 900
млн.руб., №8 – 825 млн.руб., №9 – 967,5 млн.руб., №13 – 1005 млн.руб., №14 –
1095 млн.руб., №17 – 960 млн.руб., №18 – 1140 млн.руб., №20 – 975
млн.руб., №24 – 1117,5 млн.руб., №25 –
975 млн.руб., №26 – 922,5 млн.руб., №28 – 937,5 млн.руб., №29 – 1027,5
млн.руб., №31 – 975 млн.руб., №32 – 870 млн.руб.
, включающий предприятия
с наиболее характерными значениями показателей следующий: (765,4853119;
1191,014688) 19 предприятие, вошедшие в этот диапазон, следующие: №1 – 772,5
млн.руб., №2 – 847,5 млн.руб., №3 – 945 млн.руб., №4 – 1050 млн.руб., №6 – 900
млн.руб., №8 – 825 млн.руб., №9 – 967,5 млн.руб., №13 – 1005 млн.руб., №14 –
1095 млн.руб., №17 – 960 млн.руб., №18 – 1140 млн.руб., №20 – 975
млн.руб., №24 – 1117,5 млн.руб., №25 –
975 млн.руб., №26 – 922,5 млн.руб., №28 – 937,5 млн.руб., №29 – 1027,5
млн.руб., №31 – 975 млн.руб., №32 – 870 млн.руб.
3.
Насколько сильны различия в экономических характеристиках предприятий
выборочной совокупности? Можно ли утверждать, что выборка сформирована из
предприятий с достаточно близкими значениями по каждому из показателей?
По
среднегодовой стоимости основных производственных фондов различия в
экономических характеристиках предприятий составляют 17,14971977%; выборка
количественно однородна по данному признаку, то есть, она сформирована из
предприятий с достаточно близкими значениями6 максимальное расхождение в
значениях составляет 750 млн.руб.
По выпуску продукции различия в
экономических характеристиках предприятий составляют 21,74952089 %; выборка
количественно однородна по данному признаку, то есть, она сформирована из
предприятий с достаточно близкими значениями: максимальное расхождение в
значениях составляет 900 млн.руб.
4.Какова структура предприятий выборочной
совокупности по среднегодовой стоимости основных фондов? Каков удельный вес
предприятий с наибольшими, наименьшими и типичными значениями данного
показателя? какие именно это предприятия?
Структура предприятий выборочной
совокупности по среднегодовой стоимости основных производственных фондов
представлена в таблице 7. Наиболее типичные значения данного показателя – от
965 до 1115 млн.руб. Удельный вес предприятий с указанными значениями
составляет 66,67%. Это следующие 11 предприятий: №3 – 972,5 млн.руб., №4 – 1025
млн.руб., №6 – 1077,5 млн.руб., №7 – 1107,5 млн.руб., №9 – 1017,5 млн.руб., №13
– 980 млн.руб., №14 – 1077,5 млн.руб., №17 – 1055 млн.руб., №25 – 1077,5
млн.руб., №26 – 1002,5 млн.руб., №28 – 1047,5 млн.руб.
Интервал с наибольшими значениями данного
показателя – от 1265 до 1415 млн.руб. Удельный вес предприятий с указанными значениями составляет 100%. Это
следующие 3 предприятия: №12 – 1287,5 млн.руб., №16 – 1415 млн.руб., №21 –
1317,5 млн.руб.
Интервал с наименьшими значениями данного
показателя – от 665 до 815 млн.руб. Удельный вес предприятий с указанными значениями составляет 13,33%.
Это следующие 4 предприятия: №1 – 800 млн.руб., №5 – 665 млн.руб., №23 – 717,5
млн.руб., №27- 777,5 млн.руб.
На основе анализа можно сделать вывод о
том, что большинство предприятий сосредоточенны в модальном интервала, то есть
в интервале с наиболее типичными значениями изучаемого показателя.
5. Носит ли распределение предприятий по группам закономерный
характер и какие предприятия (с более высокой или более низкой стоимостью
основных фондов) преобладают в совокупности?
Гистограмма
распределения предприятий по стоимости основных производственных фондов
представлена на рисунке1. По данной гистограмме визуально устанавливаем, что в
распределении единиц совокупности прослеживается такая закономерность, на
основании которой можно сделать вывод о близости эмпирического распределения к
нормальному.
Согласно таблице 8, показатель ассиметрии
по данному показателю равен -0,21025237. Следовательно, имеет место
незначительная левосторонняя ассиметрия, то есть в совокупности преобладают
предприятия с более низкой среднегодовой стоимостью основных производственных
фондов.
6.
каковы ожидаемые средние величины среднегодовой стоимости основных фондов и
выпуска продукции на предприятиях корпорации в целом? Какое максимальное
расхождение в значениях показателя можно ожидать?
Ожидаемая средняя величина среднегодовой
стоимости основных производственных фондов будет находиться в интервале
(1006,27695; 1073,7230) с вероятностью
0,683, в интервале (970,95086; 1109,0491)
с вероятностью 0,954, в интервале (932,71075; 1147,289) с вероятностью 0,997. Ожидаемый размах вариации по данному
показателю, то есть прогнозное максимальное расхождение в значениях данного
показателя составляет 1070 млн.руб.
Ожидаемая средняя величина выпуска продукции будет находиться в
интервале (938,021302; 1018,47869)
с вероятностью 0,683, в интервале (895,8803078; 1060,61969) с вероятностью 0,954, в интервале (850,2631419; 1106,23685) с вероятностью 0,997. Ожидаемый
размах вариации по данному показателю, то есть прогнозное максимальное
расхождение в значениях данного показателя составляет 1276 млн.руб.