4. Замкнутый резервуар разделен на две
части плоской перегородкой, имеющей квадратное отверстие со стороной а=400 мм,
закрытое крышкой. Давление над жидкостью Ж (керосин) в левой части резервуара
определяется показателем манометра Рм = 0,07 МПа (абс); давление
воздуха в правой части – показателем мановаккуумметра Рв = 0,02 МПа (абс).
Определить величину и точку приложения результирующей силы давления на крышку.
Расстояние от поверхности жидкости до крышки h=1300 мм.
Указание: Эксцентриситет центра давления для результирующей силы:
.
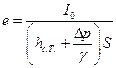Решение: Сила давления на плоскую вертикальную стенку равна произведению давления
в геометрическом центре на площадь поверхности. Геометрический центр крышки
находится от поверхности жидкости на расстоянии h + a/2. Давление керосина на этой глубине
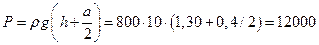Па.
Тогда величина
результирующей силы давления:
.
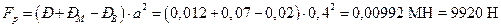Эксцентриситет центра
давления для результирующей силы:
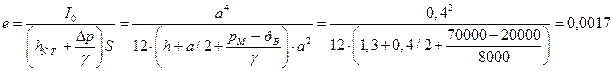м.
Тогда точка приложения результирующей
силы к крышке находится на высоте h+a/2+е=1,3+0,2+0,0017=1,5017 м.
Ответ: 9920Н;
1,5017 м.
13.
На поршень диаметром D = 250 мм действует сила F = 7∙104 H. Определить скорость движения
поршня, если в цилиндре находится вода, диаметр отверстия в поршне d = 12 мм, толщина поршня а =
55 мм. Силой трения поршня о стенки цилиндра пренебречь, давление жидкости на
верхнюю плоскость поршня не учитывать.
Решение: Давление, которое поршень производит в сосуде, найдем как произведение
силы на площадь цилиндра, т.е.
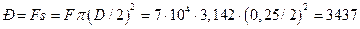Па.
Пусть коэффициент
гидравлического трения воды о стенки «трубы» – отверстия в поршне – равен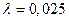 
. Тогда коэффициент сопротивления по длине этой «трубы» равен
.
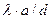Если бы отверстие было бы
не в цилиндре, а в боковой стенке сосуда, то такое давление достигалось бы в
центре этого отверстия на глубине:
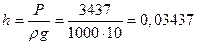м.
Причем расход воды тот
же, независимо от того, в цилиндре отверстие, или в боковой стенке сосуда, т.е.
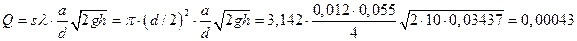м3/с.
Тогда скорость течения
воды через отверстие в поршне найдется так:
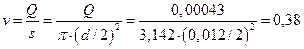м/с.
Скорость движения поршня
в D/d раз меньше скорости движения воды
через отверстие. Тогда искомая скорость движения поршня:
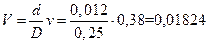м/с.
Ответ: 0,01824 м/с.
14.
Определить длину трубы l, при которой расход жидкости из бака будет ровно в
два раза меньше, чем через отверстие того же бака диаметра d = 70 мм. Напор над отверстием
равен Н = 4 м. Коэффициент
гидравлического трения .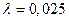
Решение: По формуле Торричелли, расход жидкости через отверстие площадью s равен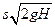 
. Если делать поправку на сопротивление по длине, то формула
Торричелли изменится: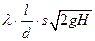 
.
Так как, по условию
задачи, расход жидкости из бака будет ровно в два раза меньше, чем через
отверстие того же бака, то выразим искомую длину трубы из уравнения:
=
.
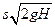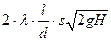Откуда искомая длина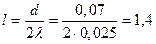 
м.
Ответ: 1,4 м.
25.
Определить производительность и напор насоса (рабочую точку) при подаче воды в
открытый резервуар из колодца на геодезическую высоту Нг = 6 м по
трубопроводу диаметром d = 250 мм, длиной l = 40 м, с коэффициентом
гидравлического трения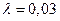 
и эквивалентной
длинной местных сопротивлений le = 8 м. Как изменится подача и напор
насоса, если частота вращения рабочего колеса уменьшится на 10%?
Решение: Предположим, что насос развивает максимальную производительность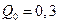 
м3/с. При этом насос подает воду в открытый
резервуар из колодца на геодезическую высоту Нg = 6 м по трубопроводу диаметром d = 250 мм, длиной l = 40 м, с коэффициентом гидравлического
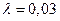трения и эквивалентной
длинной местных сопротивлений le = 8 м.
Максимальный напор насоса
найдется из соотношения:
.
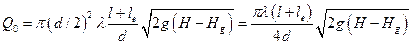Выразим из этого
соотношения максимальный напор и подставим численные значения:
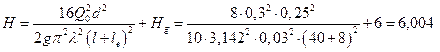м.
При расчете подачи и
напора насоса при изменении частоты вращения рабочего колеса на 10% следует
иметь в виду, что в таблице с исходными данными показана производительность
насоса с шагом 20%. Для ответа на поставленный вопрос составим таблицу с шагом
10%, исходя их предположения о линейной связи
Q – H на каждом 20%-ом отрезке; тогда
соответствующие коэффициенты в точках 0,1, 0,3, 0,5, 0,7, 0,9 найдутся как
средние арифметические соседних коэффициентов при Н:
|
|
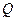
0
|
0.1
|
0.2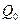
|
0.3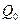
|
0,4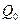
|
0,5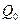
|
0,6
|
0,7
|
0,8
|
0,9
|
|
|
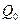
H
|
|
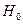
1,025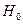
|
1,05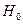
|
1,025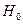
|
|
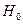
1,44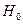
|
1,88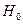
|
1,265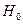
|
0,65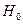
|
0,5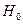
|
0,35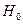
|
Так, при снижении
производительности с максимальной до 90% напор увеличится и составит:
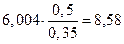м.
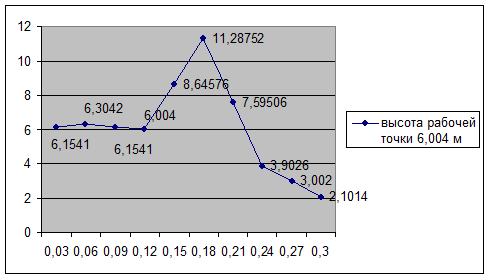
Подставим значения Q – H в таблицу, начертим график и покажем
на нем рабочую точку насоса.
|
Q
|
0,03
|
0,06
|
0,09
|
0,12
|
0,15
|
0,18
|
0,21
|
0,24
|
0,27
|
0,3
|
|
H
|
6,1541
|
6,3042
|
6,1541
|
6,004
|
8,64576
|
11,28752
|
7,59506
|
3,9026
|
3,002
|
2,1014
|
28. Определить средний объемный коэффициент полезного действия, максимальную
теоретическую подачу и степень неравномерности подачи поршневого насоса
двойного действия и диаметром цилиндра D = 100 мм, ходом поршня S = 60 мм, диаметром штока d = 25 мм, при n = 60 (об/мин) двойных ходах в минуту, заполняющего мерный бак
W = 0.077 м3 за t = 100 с.
Решение:
Действительная производительность
насоса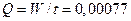 
м3/сек. Максимальная теоретическая
производительность насоса двойного действия будет
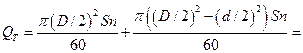
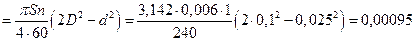м3/сек.
Отношение
действительной подачи Q к теоретической QT называется
объемным КПД поршневого насоса:
.
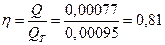Степень неравномерности
подачи насоса можно принять для одноцилиндрового – 3,14, а для двухцилиндрового
– 1,57.
Ответ: средний объемный коэффициент полезного действия 0,81; максимальная теоретическая производительность насоса 0,95; степень
неравномерности подачи насоса – 1,57.
34.
Определить полезную мощность насоса объемного действия гидропривода, если
внешняя нагрузка на поршень силового гидроцилиндра F = 70000 H, скорость рабочего хода v = 12,5 см/с, диаметр поршня D1 = 130 мм, диаметр штока D2 = 44 мм. Механический коэффициент
полезного действия гидроцилиндра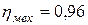 
, объемный коэффициент полезного действия гидроцилиндра 
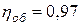. Общая длина трубопровода системы l = 12 м, диаметр трубопроводов d = 25 мм. Рабочая жидкость в системе
– спиртоглицериновая смесь (Y = 12100 Н/м3, v = 1,2 см2/с).
Указание: Напор насоса затрачивается на перемещение поршня, нагруженного силой F, и на преодоление гидравлических потерь в трубопроводах системы.
Решение: Полезную мощность насоса можно найти по двум эквивалентным формулам
,
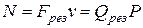где результирующая сила Fрез посчитана с учетом механических и
гидравлических потерь в трубопроводах
системы; также эти потери учитываются при расчете Qрез.
Поршень диаметром D1 = 130 мм, нагруженный силой 70000 H с учетом механических потерь,
создает давление
Р = 0,13 × 70000 × 0,96 = 8736 Па.
Значит, это давление
двигает жидкость по трубопроводу системы, развивая мощность
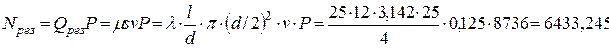Вт.
Наконец, учитывая
объемный коэффициент полезного действия, окончательно получим:
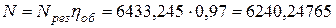Вт.
Ответ: мощность 6,14 кВт.