Содержание
Задача 6. 3
Задача 18. 4
Задача 21. 4
Задача 25. 5
Задача 30. 7
Задача 41. 7
Задача 6
Определить силу давления
на коническую крышку горизонтального цилиндрического сосуда диаметром D1=1500 мм, заполненного керосином. Показания манометра
в точке его присоединения – рм=0,4 МПА (абс).
Показать на чертеже вертикальную и горизонтальную составляющие, а также полную
силу давления. а=900 мм.
Решение:
Пусть мы имеем резервуар с наклонной правой стенкой, заполненный жидкостью с
удельным весом γ. Ширина стенки в направлении,
перпендикулярном плоскости чертежа (от читателя), равна b
(рис.2.3). Стенка условно показана развернутой относительно оси АВ и
заштрихована на рисунке. Построим график изменения избыточного
гидростатического давления на стенку АВ.
Так как избыточное гидростатическое давление изменяется по линейному закон
P=γgh, то для построения графика, называемого
эпюрой давления, достаточно найти давление в двух точках, например А и B.
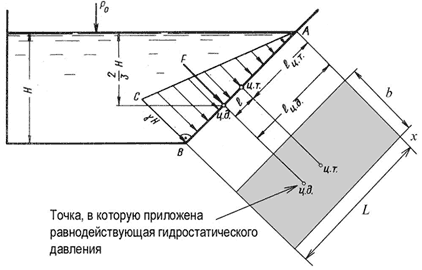
Рис. 2.3. Схема к определению равнодействующей
гидростатического давления на плоскую поверхность
Избыточное гидростатическое давление в точке А будет равно
PA = γh = γ·0 = 0
Соответственно давление в точке В:
PB = γh = γH
где H - глубина жидкости в резервуаре.
Согласно первому свойству гидростатического давления, оно
всегда направлено по нормали к ограждающей поверхности. Следовательно,
гидростатическое давление в точке В, величина которого равна γH, надо направлять перпендикулярно к стенке АВ.
Соединив точку А с концом отрезка γH,
получим треугольную эпюру распределения давления АВС с прямым углом в
точке В. Среднее значение давления будет равно
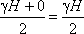
Если площадь наклонной стенки S=bL,
то равнодействующая гидростатического давления равна
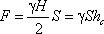
где hc = Н/2 -
глубина погружения центра тяжести плоской поверхности под уровень жидкости.
Однако точка приложения равнодействующей гидростатического
давления ц.д. не всегда будет совпадать с центром
тяжести плоской поверхности. Эта точка находится на расстоянии l от центра тяжести и равна отношению момента
инерции площадки относительно центральной оси к статическому моменту этой же
площадки.
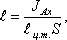
где JАx -
момент инерции площади S относительно центральной оси, параллельной Аx.
В частном случае, когда стенка имеет форму прямоугольника
размерами bL и одна из его сторон лежит на
свободной поверхности с атмосферным давлением, центр давления ц.д. находится на расстоянии b/3
от нижней стороны.
Задача 18
При внезапном расширении
трубопровода скорость жидкости в трубе большего диаметра равна v=2,5 м/с. Отношение диаметров труб D:d=2. Определить h
– разность показаний
пьезометров.
Решение:
Задача 21
Определить время закрытия
задвижки, установленной на свободном конце стального водопровода диаметром d=150 мм, длиной l=1700 м, с толщиной стенки d=8 мм.,
при условии, чтобы максимальное повышение давления в водопроводе было в три
раза меньше, чем при мгновенном закрытии задвижки. Через сколько времени после
мгновенного закрытия задвижки повышение давления распространится до сечения,
находящегося на расстоянии 0,7l от задвижки?
Решение:
Скачок давления
распространяется по трубе в виде упругой волны со скоростью u , определяемой коэффициентом
сжимаемости и плотностью жидкости, модулем упругости материала трубы, ее
диаметром и толщиной стенок. Для потоков воды в стальных и чугунных трубах u ” 1000 – 1350 м/с.
Если жидкость плотности
? течет со
скоростью v
в трубопроводе с площадью сечения
S , а задвижка в конце трубопровода закрывается
за время (?t)з , то возникает увеличение давления ?p . В прилегающем к задвижке слое жидкости
длиной ?l=
u(?t)з и массой m=?S?l, теряется импульс ?(mv)=?S?lv. По второму закону Ньютона изменение импульса
определяется величиной действующей силы: ?(mv)/
(?t)з = F. Учитывая, что
F =?pS , получаем выражение для
величины скачка давления:
?p
= ?vu (1)
Образующееся при гидравлическом ударе повышение давления
распространяется против течения жидкости и
через время L/u
( L -длина трубопровода)
достигает резервуара. Здесь давление падает, и это падение давления передается
обратно к задвижке с той же скоростью в виде отраженной волны (волна понижения).
Циклы повышений и понижений давления чередуются через промежутки времени 2L/u , пока этот колебательный процесс не затухнет из-за
потерь энергии на трение и деформацию стенок.
Формула
(1) действительна лишь в случае,
когда время закрытия запорного устройства сравнительно мало, т.е. при условии (?t)з
<< 2L/u. При (?t)з
> 2L/u отраженная волна придет к
запорному устройству раньше, чем задвижка закроется, и повышение давления в
трубопроводе уменьшится. В этом случае величина скачка давления:
Задача 25
Определить
производительность и напор насоса (рабочую точку) при подаче воды в открытый
резервуар из колодца на геодезическую высоту Нг
= 6 м по трубопроводу диаметром d = 250 мм, длиной l = 40 м, с коэффициентом
гидравлического трения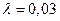 
и эквивалентной
длинной местных сопротивлений lэкв = 8 м. Как изменится подача и напор
насоса, если частота вращения рабочего колеса уменьшится на 10%?
Решение:
Предположим, что насос
развивает максимальную производительность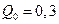 
м3/с. При этом насос подает воду в открытый
резервуар из колодца на геодезическую высоту Нг
= 6 м по трубопроводу диаметром d = 250 мм, длиной l = 40 м, с коэффициентом гидравлического
трения 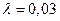и эквивалентной
длинной местных сопротивлений lэкв = 8 м.
Максимальный напор насоса
найдется из соотношения:
.
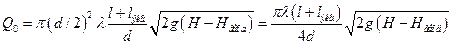Выразим из этого
соотношения максимальный напор и подставим численные значения:
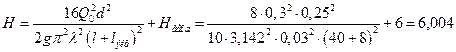Н.
При расчете подачи и
напора насоса при изменении частоты вращения рабочего колеса на 10% следует
иметь в виду, что в таблице с исходными данными показана производительность
насоса с шагом 20%. Для ответа на поставленный вопрос составим таблицу с шагом
10%, исходя их предположения о линейной связи
Q – H на каждом 20%-ом отрезке; тогда
соответствующие коэффициенты в точках 0,1, 0,3, 0,5, 0,7, 0,9 найдутся как
средние арифметические соседних коэффициентов при Н:
|
|
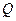
0
|
0.1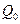
|
0.2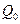
|
0.3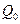
|
0,4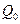
|
0,5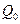
|
0,6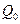
|
0,7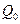
|
0,8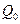
|
0,9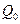
|
|
|
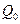
H
|
|
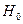
1,025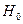
|
1,05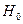
|
1,025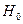
|
|
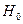
1,44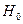
|
1,88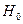
|
1,265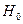
|
0,65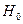
|
0,5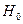
|
0,35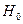
|
Так, при снижении
производительности с максимальной до 90% напор увеличится и составит:
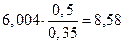м.
Задача 30
Поршневой насос простого
действия с диаметром цилиндра D=90 мм, ходом поршня S=260 мм, числом двойных ходов в
минуту п=75 ход/мин и объемным КПД hоб=0,9 подает рабочую жидкость в
систему гидропровода. При какой частоте вращения
должен работать включенный параллельно шестеренный насос с начальным диаметром
шестерен d=72 мм, шириной шестерен b=65 мм, числом зубьев z=30 и объемным КПД hоб=0,86, чтобы количество подаваемой
жидкости удвоилось?
Решение:
Давление на выходе: номинальное r1н=16МПа;
максимальное r1мак=20МПа
минимальная частота вращения вала nмин=16с-1
|
Показатели
|
НШ10-3
|
НШ32А-3
|
НШ50А-3
|
НШ71А-3
|
НШ100А-3
|
НШ250-3
|
|
Рабочий
объем, см3
|
10
|
31,5
|
48,8
|
69,7
|
98,8
|
250
|
|
Частота
вращения вала, с-1
номинальная
максимальная
|
40
50
|
32
40
|
32
40
|
25
32
|
25
32
|
25
32
|
|
Номинальная
объемная подача, дм3/мин
|
22,1
|
55,6
|
86,2
|
98,3
|
139,3
|
352,3
|
|
Номинальная
потребляемая мощность, кВт
|
6,9
|
17,6
|
26,2
|
30,5
|
43,2
|
106,2
|
|
КПД:
полный
объемный
|
0,85
0,92
|
0,83…0,87
0,92…0,97
|
0,82…0,9
0,92…0,97
|
0,85…0,88
0,94…0,98
|
0,85…0,88
0,94…0,98
|
0,85…0,88
0,94…0,98
|
|
Масса,
кГ
|
2,5
|
6,8
|
7,5
|
16,8
|
16,8
|
45,6
|
Примечание. Значения показателей
определены при работе насосов в номинальном режиме на минеральном масле
вязкостью 60…70 мм2/с.
Задача 41
Пользуясь
характеристикой, приведенной в задаче 40, определить активный диаметр и
построить внешнюю (моментальную) характеристику гидромуфты, предназначенной для
работы с асинхронным электродвигателем, развивающим максимальный крутящий
момент М=350 Н×м
при частоте вращения п=1100 об/мин.
Рабочая жидкость – минеральное масло.
Указание: Активный диаметр может быть определен по уравнению моментов совмещением
режимов гидромуфты при l=0 и электродвигателя при максимальном
моменте М.
Решение: