Лабораторная работа №2
Цель работы: изучение особенностей использования СИ с различными способами нормирования пределов допускаемой основной погрешности.
Особенности СИ определяют способ нормирования пределов допускаемой основной погрешности:
Диапазон измерений — область значений величины, в пределах которых нормированы допускаемые пределы погрешности. Значения величины, ограничивающие диапазон измерений снизу или сверху (слева и справа), называют соответственно нижним или верхним пределом измерений.
Порог чувствительности — наименьшее изменение измеряемой величины, которое вызывает заметное изменение выходного сигнала. Например, если порог чувствительности весов равен 10 мг, то это означает, что заметное перемещение стрелки весов достигается при таком малом изменении массы, как 10 мг.
Класс точности СИ — обобщенная характеристика, выражаемая пределами допускаемых (основной и дополнительной) погрешностей, а также другими характеристиками, влияющими на точность. Классы точности конкретного типа СИ устанавливают в НД. При этом для каждого класса точности устанавливают конкретные требования к метрологическим характеристикам, в совокупности отражающим уровень точности СИ данного класса. Например, для вольтметров нормируют предел допускаемой основной погрешности и соответствующие нормальные условия; пределы допускаемых дополнительных погрешностей; пределы допускаемой вариации показаний; невозвращение указателя к нулевой отметке. У плоскопараллельных концевых мер длины такими характеристиками являются пределы допускаемых отклонений от номинальной длины и плоскопараллельности; пределы допускаемого изменения длины в течение года. У мер электродвижущей силы (нормальных элементов) нормируют пределы допускаемой нестабильности ЭДС в течение года.
Обозначение классов точности осуществляется следующим образом.
Если пределы допускаемой основной погрешности выражены в форме абсолютной погрешности СИ, то класс точности обозначается прописными буквами римского алфавита. Классам точности, которым соответствуют меньшие пределы допускаемых погрешностей, присваиваются буквы, находящиеся ближе к началу алфавита.
Для СИ, пределы допускаемой основной погрешности которых принято выражать в форме относительной погрешности, обозначаются числами, которые равны этим пределам, выраженным в процентах. Так, класс точности 0,001 нормальных элементов свидетельствует о том, что их нестабильность за год не превышает 0,001%. Обозначения класса точности наносят на циферблаты, щитки и корпуса СИ, приводят в НД. СИ с несколькими диапазонами измерений одной и той же физической величины или предназначенным для измерений разных физических величин могут быть присвоены различные классы точности для каждого диапазона или каждой измеряемой величины. Так, электроизмерительному прибору, предназначенному для измерений напряжения и сопротивления, могут быть присвоены два класса точности: один как вольтметру, другой как омметру.
Задание:
Собираем следующую схему:
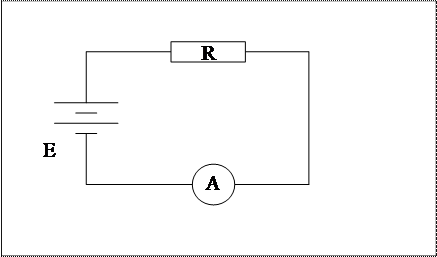
где Rx – сопротивление, Е – источник тока, А – амперметр класса точности 1 с пределом измерения = 5 мА, с ценой деления = 0,01мА.
Строим таблицу показаний реального амперметра класса точности 1.0 для суммарного сопротивления цепи R в диапазоне от 10 кОм до 1 кОм:
|
Суммарное сопротивление R (Ом) |
Ток I (мА) |
|
10 |
0,99 |
|
8 |
1,24 |
|
6 |
1,65 |
|
4 |
2,24 |
|
2 |
4,99 |
Абсолютная погрешность рассчитывается по формуле:
Δ = (Xo – Xиз)*100%/Xo,
где Хо – идеальное значение,
Хиз – реальное значение.
Относительная погрешность рассчитывается по формуле:
δ = Δ/Хо,
Точность измерения определяется по формуле:
Т = 1/ δ.
Результаты вычислений заносим в таблицу:
|
Δ (%) |
δ (%) |
Т |
|
1 |
1 |
1 |
|
1 |
0.8 |
1.25 |
|
1 |
0.6 |
1.6 |
|
1 |
0.44 |
2.27 |
|
1 |
0.2 |
5 |
График зависимости абсолютной погрешности от показаний амперметра:
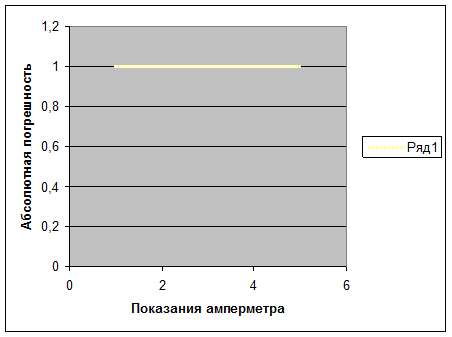
График зависимости относительной погрешности от показаний амперметра:
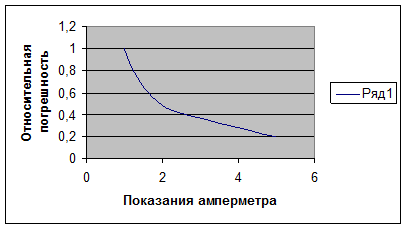
График зависимости точности измерения от показаний амперметра:
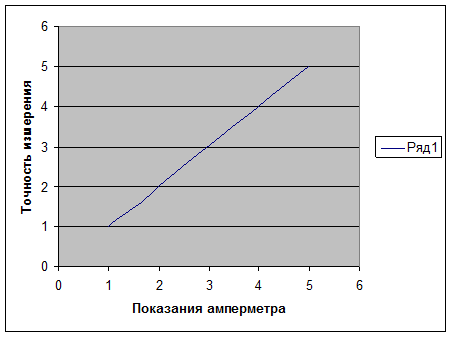
Из полученных графиков можно сделать вывод: точность измерения СИ в данном случае наиболее высока при измерении больших значений величин, а относительная погрешность высока при измерении малых величин.
Класс точности 1,0/0,2 – подразумевает под собой наличие омметра и амперметра в одном устройстве, где класс точности амперметра = 1,0, а омметра = 0,2.
Для амперметра этого класса точности можно использовать данные, полученные выше. Для омметра, с классом точности 0,2, пределом измерения 10 кОм, с ценой деления 1 Ом собираем следующую схему и снимаем только одно значение (т.к. принципиальная схема работы омметра не отличается от принципиальной схемы работы амперметра).
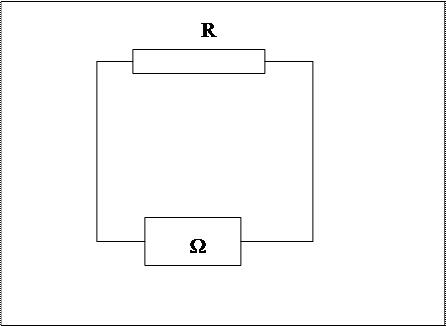
При установке сопротивления R = 5 кОм, омметр показывает 5010 Ом.
Следовательно, абсолютная погрешность равна 0,2%. Относительная погрешность в начальной точке шкалы (1 кОм) равна 0,2%, а в конечной (10 кОм) – 0,02%. Точность измерения в начальной точке = 5, в конечной = 50.
Отсюда делаем вывод:
Точность СИ увеличивается при измерении величин, приближающихся к пределу измерения прибора.
Предел измерения прибора выбирается в зависимости от измеряемой величины, т.е. максимальное значение измеряемой величины должно стремиться к пределу измерения прибора.
Задание:
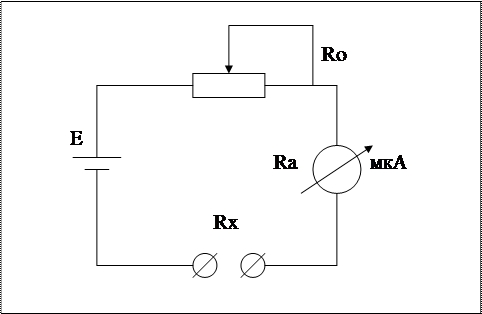
Е = 3В, Re = 0, Ro = 29кОм, Ra = 1кОм, Rx = 0.
Основное звено схемы – микроамперметр, работающий в режиме омметра. При Rx = 0 – омметр показывает ноль (микроамперметр показывает 100 мкА). При увеличении Rx – стрелка прибора отклоняется влево (в сторону 0 по шкале микроамперметра).
Формула для делений омметра следующая (исходя из закона Ома):
100-n = E*106/(Ro+Ra+Rx),
где 100-n – градуировка омметра «с конца» на 100 делений, 106 – коэффициент перехода от «микро» к нормальным измерениям.
Отклонение на 1 деление соответствует включению в цепь сопротивления, равного:
100-1 = 3*1000000/(1000+29000+х)
х = 3000000/99 – 30000 = 303 Ом
Отклонение на 99 делений соответствует включению в цепь сопротивления, равного:
100-99 = 3*1000000/(1000+29000+х)
х = 3000000/1 – 30000 = 2,97 МОм
Градуировочная таблица:
|
n, дел |
0 |
50 |
67 |
75 |
80 |
|
Rx, Ом |
0 |
30000 |
60000 |
90000 |
120000 |
Изображение шкалы:
|

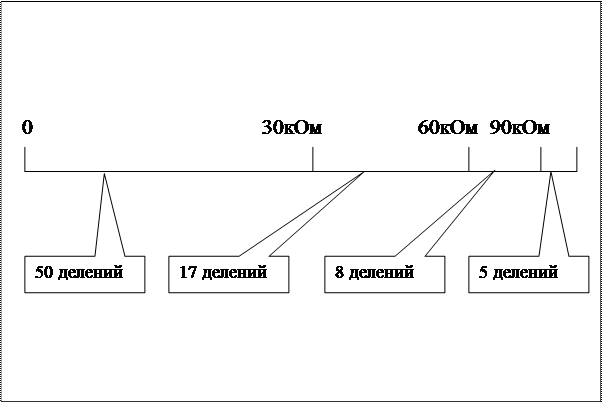
Для расчета абсолютной погрешности будем использовать следующие точки шкалы:
10000Ом = 25 дел.
20000Ом = 40 дел.
30000Ом = 50 дел.
40000Ом = 57 дел.
50000Ом = 63 дел.
60000Ом = 67 дел.
70000Ом = 70 дел.
80000Ом = 73 дел.
90000Ом = 75 дел.
100000Ом = 77 дел.
Для этой шкалы погрешность рассчитывается по принципу ±1 деление. То есть ∆R=|Ri-Ri±1|. Для дальнейших расчетов берется значение большее по модулю.
Так как шкала неравномерна только в одну сторону, большее значение будет в сторону возрастания значений шкалы.
|
∆, % |
δ, % |
T |
|
|
26 дел. = 10540 Ом |
5,4 |
0,054 |
18,5 |
|
41 дел. = 20847 Ом |
4,2 |
0,021 |
47,6 |
|
51 дел. = 31224 Ом |
4,1 |
0,014 |
72,4 |
|
58 дел. = 41428 Ом |
3,6 |
0,009 |
111,1 |
|
64 дел. = 53333 Ом |
6,7 |
0,013 |
77 |
|
68 дел. = 63750 Ом |
6,2 |
0,01 |
100 |
|
71 дел. = 73448 Ом |
4,9 |
0,007 |
142,9 |
|
74 дел. = 85384 Ом |
6,7 |
0,008 |
125 |
|
76 дел. = 95000 Ом |
5,6 |
0,006 |
166,7 |
|
78 дел. = 106363 Ом |
6,4 |
0,006 |
166,7 |
График абсолютной погрешности по шкале омметра:
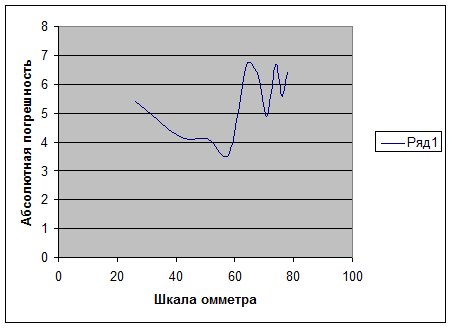
График относительной погрешности по шкале омметра:
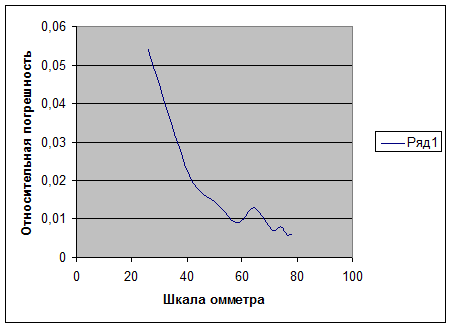
График точности измерений по шкале омметра:
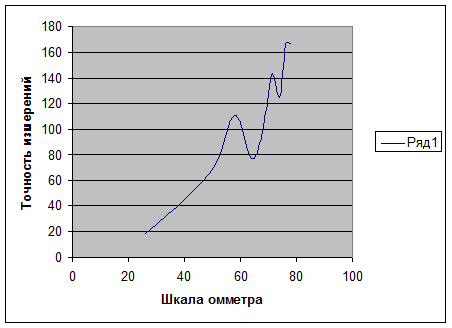
Выводы: анализируя графики полученные для СИ с линейной шкалой и графиков для СИ с резко нелинейной шкалой можно сказать, что характер погрешностей и точности измерения принципиально не меняется.
Точно так же не изменится характер погрешностей и точности измерения для параллельной схемы омметра. В этой схеме изменится предел измерения, т.е. резко уменьшится. Соответственно несколько увеличится точность измерений.
Параллельную схему целесообразно применять для измерения небольших значений сопротивления, последовательную же для больших значений.
Порядок действий при определении абсолютной погрешности результата измерения в единицах измеряемой величины (в Омах) любым из двух омметров при реальном использовании прибора, когда уравнение шкалы неизвестно, а имеется только шкала реального омметра и известны: отсчет по шкале для измеряемого сопротивления; класс точности омметра и длина его шкалы:
1. Определяем общее количество делений шкалы.
2. Вычисляем по формуле погрешность шкалы:
∆l = кл.точ.*lшк./100%
3. Вычисляем по шкале сопротивление, соответствующее погрешности, вычисленной в предыдущем пункте.
4. Абсолютная погрешность результата измерения в единицах измеряемой величины вычисляется по формуле:
∆R=Rпогр.-Rизм.