КАФЕДРА СТАТИСТИКИ

О Т Ч Е Т

о результатах выполнения

компьютерной лабораторной работы №2

«Автоматизированный априорный анализ статистической совокупности

 в среде MS Excel»

Вариант № 14

Выполнил: ст. III курса гр.________________

Проверил:______________________________

Уфа 2007 г.

1. Постановка задачи

Корреляционно-регрессионный анализ (КР-анализ) взаи­мосвязи признаков является составной частью проводимого ста­тистического исследования двух экономических показателей ста­тистической совокупности 32 предприятий и частично использует результаты Лабораторной работы № 1.

В Лабораторной работе № 2 изучается взаимосвязь меж­ду факторным признаком Среднегодовая стоимость основных производственных фондов (признак X) и результативным призна­ком Выпуск продукции (признак У), значениями которых являются исходные данные Лабораторной работы № 1 после исключения из них аномальных значений (табл.1).

Таблица 1

Исходные данные

В процессе статистического исследования необходимо ре­шить ряд задач.

1.Установить наличие статистической связи между фактор­ным признаком Х и результативным признаком Y:

а)графическим методом;

б)методом сопоставления параллельных рядов.

2.Установить наличие корреляционной связи между призна­ками Х и Y методом аналитической группировки.

3.Оценить тесноту связи признаков Х и Y на основе:

а)эмпирического корреляционного отношения ŋ;

б)линейного коэффициента корреляции r.

4.Построить однофакторную линейную регрессионную мо­дель связи признаков X и Y, используя инструмент Регрессия над­стройки Пакет анализа.

5. Найти наиболее адекватное нелинейное уравнение регрес­сии с помощью средств инструмента Мастер диаграмм. Построить для этого уравнения теоретическую кривую регрессии.

2. Рабочий файл с результативными таблицами и графиками

3. Выводы по результатам выполнения лабораторной работы.

1. Установление наличия стохастической связи между факторным признаком Х и результативным признаком Y:

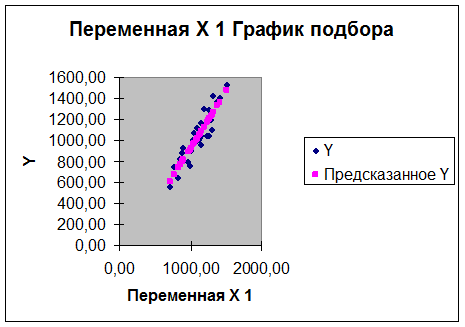
     а) графическим методом.

     На основе анализа диаграммы рассеяния из Лабораторной  работы № 1, полученной после удаления аномальных значений, можно сделать вывод, что имеет (не имеет) место стохастическая связь. Предположительный вид связи: линейная (нелинейная) прямая (обратная).

     б) методом сопоставления параллельных рядов.

     Табл.2.1, полученная путем ранжирования предприятий по возрастанию значения факторного признака Х, показывает, что с увеличением значений факторного признака увеличиваются (уменьшаются) значения результативного признака, за исключением некоторых отклонений от общей тенденции, что позволяет сделать вывод о наличии стохастической связи.

2. Установление наличия корреляционной связи между признаками Х и Y методом аналитической группировки.

     Результаты выполнения аналитической группировки предприятий по факторному признаку Среднегодовая стоимость основных производственных фондов даны в табл. 2.2 Рабочего файла, которая показывает, что существует корреляционная связь между Среднегодовой стоимостью основных производственных фондов и Выпуском продукции.

3. Оценка тесноты связи признаков Х и Y:

     а) на основе эмпирического корреляционного отношения.

     Для анализа тесноты связи между факторным и результативным признаками, рассчитывается показатель η - эмпирическое корреляционное отношение, задаваемое формулой :    .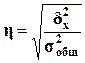

     Для вычисления η необходимо знать общую диспе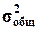рсию  и межгрупповую дисперсию 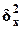 результативного признака Y - Выпуск продукции.

Результаты выполненных расчетов представляются табл. 2.4 Рабочего файла.Величина η=0,90 является близкой к единице, что свидетельствует о тесной связи между факторным и результативным признаками.

     б) на основе линейного коэффициента корреляции признаков.

В предположении, что связь между факторным и результативным признаками прямолинейная, для определения тесноты связи на основе линейного коэффициента корреляции r был использован инструмент Корреляция надстройки Пакет анализа.

Результатом работы инструмента Корреляции является табл. 2.5 Рабочего файла. Значение коэффициента корреляции r=0,91 лежит в интервале 0,9-0,99, что в соответствии со шкалой Чэддока, говорит о весьма тесной связи между факторным и результативным признаками.

    Так как значение коэффициента корреляции r положительное, то связь между признаками прямая.

    Посредством показателя η измеряется теснота связи любой формы, а с помощью коэффициента корреляции r – только прямолинейная, следовательно, значения η и r совпадают только при наличии прямолинейной связи. В теории статистики установлено, что если 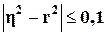, то гипотезу о прямолинейной связи можно считать подтвержденной.

Теснота связи между факторным и результативным признаками весьма значительна.

4. Построение однофакторной линейной регрессионной модели связи изучаемых признаков с помощью инструмента Регрессия надстройки Пакет анализа.

Построение регрессионной модели заключается в определении аналитического выражения связи между факторным признаком X и результативным признаком Y.

5. Регрессионные модели связи

     Инструмент Регрессия производит расчет параметров а₀ и а₁ уравнения однофакторной линейной регрессии 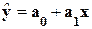 и проверку его адекватности исследуемым фактическим данным.

     В результате работы инструмента Регрессия были получены результативные таблицы 2.6 – 2.9 Рабочего файла.

     Однофакторная линейная регрессионная модель связи факторного и результативного признаков имеет вид прямой.

6. Нахождение наиболее адекватного уравнения регрессии с помощью средств инструмента Мастер диаграмм. Построение для этого уравнения теоретической линии регрессии.

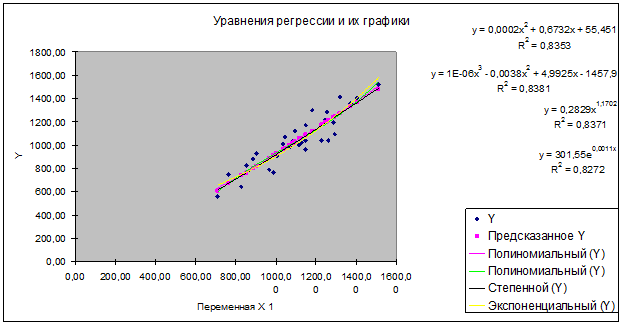
    Уравнения регрессии и их графики построены для 4-х видов нелинейной зависимости между признаками и представлены на диаграмме 2.1 Рабочего файла.

   Уравнения регрессии и соответствующие им коэффициенты детерминации R² приведены в следующей таблице:

     Выбор наиболее адекватного уравнения регрессии определяется максимальным значением коэффициента детерминации R²: чем ближе значение R² к единице, тем более точно регрессионная модель соответствует фактическим данным.

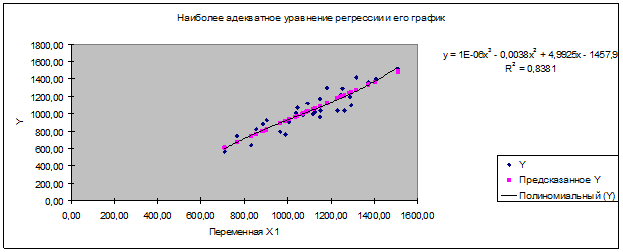
Вывод: Максимальное значение коэффициента детерминации R² =0,8381

Вид искомого уравнения регрессии – полином третьего порядка.

Это уравнение регрессии и его график приведены на отдельной диаграмме рассеяния 2.2 Рабочего файла.