Лабораторная работа №1
Изучение методических погрешностей при прямых и косвенных измерениях.
Часть 1 – изучение методических
погрешностей при прямых измерениях.
Цель работы: изучение
методических погрешностей при прямых измерениях.
Приборы и материалы:
ПК с установленной программой Electronic WorkBench, калькулятор.
1)
Собираем следующую схему в программе Electronic WorkBench:
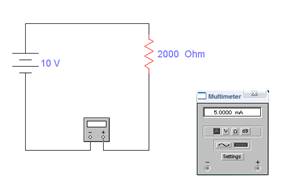
Параметры
источника тока:
Е = 10 В, r1 = 10 Ом.
Параметры резистора:
Rh = 2000 Ом.
Показания мультиметра I
= 5 мА.
Идеальная схема.
2)
Подключаем к этой дополнительное сопротивление Rа = 200 Ом последовательно с
мультиметром, работающем в режиме амперметра, для
имитации реальных условий эксперимента:
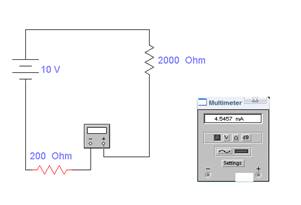
В этом случае
мультиметр показывает I
= 4,54 мА.
Абсолютная
погрешность = ΔI =
|Iидеал. – Iизмер.|/
Iидеал.*100%,
где Iидеал – теоретические
(идеальные) данные,
Iизмер
– экспериментальные данные.
ΔI = 1.2%
Относительная
погрешность = δI = ΔI/N, где
N – величина измеряемого
параметра.
δI
= 0,2%
Эта погрешность
обусловлена тем, что в схему в реальных условиях включается дополнительное
сопротивление в виде амперметра.
При Ra = 400 Ом, I = 4,16 мА, ΔI = 17%, δI = 4%
При Ra = 1000 Ом, I = 3.33мА, ΔI = 33%, δI = 10%
При Ra = 1500 Ом, I = 2.85 мА, ΔI = 43%, δI = 15%
При Ra = 2000 Ом, I = 2.5 мА, ΔI = 50%,
δI
= 20%
В результате
получаем следующую диаграмму:
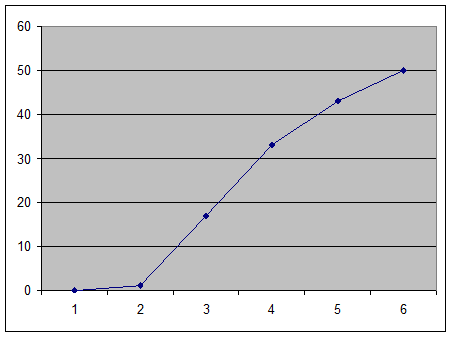
По осу Y – отложены проценты
относительной погрешности, по оси Х – отношение Ra/Rh (х0,1). График показывает, что
наиболее оптимальный выбор амперметра следует делать из расчета того, что его
внутреннее сопротивление не должно превышать измеряемое сопротивление более чем
в 0,1 раза.
3)
Собираем следующую схему:
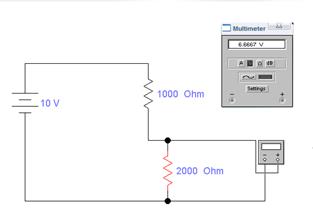
Мультиметр
работает в режиме вольметра, его внутреннее
сопротивление Rv = ∞, напряжение источника тока Е = 10 В,
сопротивление резисторов 1 и 2 кОма соответственно схеме.
Это схема идеального эксперимента. Напряжение в точках контакта вольтметра U = 6.667 В.
Для имитации
реального эксперимента добавляем параллельно вольтметру сопротивление Rv
= 20 кОм.
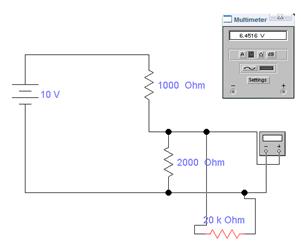
Напряжение при
этом меняется до 6,45 В.
ΔU при этом равно |Uидеал. – Uизмер.|/ Iидеал.*100% = 3%
δU
= 0.4%
При Rv
= 2 кОма, U = 5,98 В, ΔU
= 33%, δU = 10%
При Rv
= 20 кОм, U = 6,03 В,
ΔU = 4,8%, δU
= 1%
При Rv
= 200 кОм, U = 6,63 В,
ΔU = 0,4%, δU
= 0,08%
Получаем
следующий график:
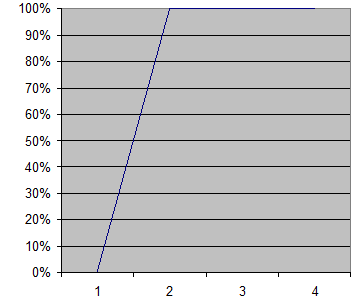
По оси Y –
относительная погрешность в процентах, по оси Х – отношение сопротивления
участка цепи, на котором ведутся измерения и сопротивления вольтметра (х0,1).
Исходя из
графика делаем вывод, что вольтметр выбирается по принципу – сопротивление
вольтметра должно быть минимум в 10 раз больше измеряемого сопротивления
участка цепи.
Часть 2 – изучение методических
погрешностей при косвенных измерениях.
Цель работы: изучение
методических погрешностей при косвенных измерениях.
1)
Собираем следующую схему:
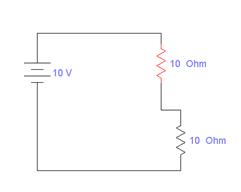
В этой схеме параллельно с одним из сопротивлений подключаем
мультиметр в режиме вольтметра, и последовательно мультиметр в режиме
амперметра. Основные характеристики схемы:
Е = 10 В, R1
= R2 = 10 Ом
(неизвестная величина из условия), сопротивление вольтметра = ∞,
сопротивление амперметра = 0.
Снимаем показания:
U =
5 В,
I =
500 мА,
Расчетное сопротивление R = 10 Ом (как и в условии, что подтверждает идеальный
эксперимент).
При той же схеме проверяем данные при R = 1000 Ом.
U =
9.901В, I = 9,901 мА,
соответственно R = 1000
Ом
Проведем
реальный эксперимент. Для этого подключим параллельно с вольтметром
сопротивление Rv = 5000 Ом, а последовательно с амперметром
сопротивление Ra = 1
Ом. Проведем эксперимент в два этапа:
а) при
сопротивлении R = 10 Ом:
I = 476,6 мА,
U = 4,75 В,
соответственно R = 9.98 Ом.
Отсюда
ΔR = 0.2%
δR =
0.02%
б) при
сопротивлении R = 1000 Ом:
I = 11,84 мА,
U = 9,8697 В,
соответственно R = 834 Ом.
Отсюда
ΔR = 16.6%
δR
= 19%
Вывод:
сопротивление амперметра не играет такой роли в этой схеме как сопротивление
вольтметра. Подключение измерительных приборов в этой схеме не принципиально,
главное чтобы были соблюдены правила их подключения.
При условии
постоянного подключения приборов можно вывести следующую формулу для расчета
относительной погрешности:
δR
= ΔR/R = |Rидеальн. – Rреальн.||Rидеальн/|Rреальн.
=
= (Rидеальн.
– Rреальн)*
Rреальн./
Rидеальн
= Rреальн.
– R2реальн/Rидеальн
Т.е. δR
= Rреальн.
– R2реальн/Rидеальн