ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ                  ИНСТИТУТ

ЭКСПРЕСС – ОТЧЕТ

о результатах выполнения лабораторной работы

по дисциплине

«Экономико-математические методы и прикладные модели»

                                         Выполнил: ст. III курса

                                      Специальность БУ, А и А

                                                          

Пенза, 2008

Задача 18

Птицефабрика реализует свою продукцию в собственной сети магазинов. В реализацию поступают как курицы различных категорий и индейки целиком, так и разделанные по частям. Вес отдельных частей и стоимость всего ассортимента продукции представлены в следующей таблице.

Изделия:

Нормы затрат

Стоимость 1 кг, руб.

Цыплята, в них, кг:

Курицы 1 категории, в них:

Курицы 2 категории, в них:

Индейки, в них, кг:

Окорочка

0,200

0,300

0,400

0,900

50

Филе

0,300

0,350

0,450

0,800

120

Крылышки

0,100

0,200

0,300

0,600

60

Субпродукты

0,050

0,100

0,200

0,300

70

Вес целиком, кг

0,650

0,950

1,350

2,600

Стоимость одного изделия целиком, руб.

38

59

89

180

Известно, что в течение дня объемы спроса ограничены следующими значениями:

Возможная реализация, кг

Ассортимент

Окорочка

Филе

Крылышки

Субпродукты

Цыплята

Курицы 1 категории

Курицы 2 категории

Индейки

Не более

150

150

150

100

100

100

200

100

Составить оптимальный ассортимент продукции, при котором объем реализации ограничен возможным спросом, а стоимость всей продукции максимальна.

Решение

1. Экономико-математическая модель задачи.

Запишем выражение целевой функции:

F(x) = (0,2х11 + 0,3х12 + 0,4х13+ 0,9х14)*50 + (0,3х21 + 0,35х22 + 0,45х23 + 0,8х24)*120 + (0,1х31 + 0,2х32 + 0,3х33 + 0,6х34)*60 + (0,05х41 + 0,1х42 + 0,2х43 + 0,3х44)*70 + 38х1 + 59х2 + 89х3 + 180х4 → max.

Ограничения:

0,2х11 + 0,3х12 + 0,4х13 + 0,9х14 ≤ 150

0,3х21 + 0,35х22 + 0,45х23 + 0,8х24 ≤ 150

0,1х31 + 0,2х32 + 0,3х33 + 0,6х34 ≤ 150

0,05х41 + 0,1х42 + 0,2х43 + 0,3х44 ≤ 100

38х1 ≤ 100

59х2 ≤ 100

89х3 ≤ 200

180х4 ≤ 100

В данной задаче оптимизационные значения вектора Х будут помещены в ячейках В5:Е9, оптимальное значение целевой функции будет находиться в ячейке А2. Расположение исходных данных представлено на рис. 1.

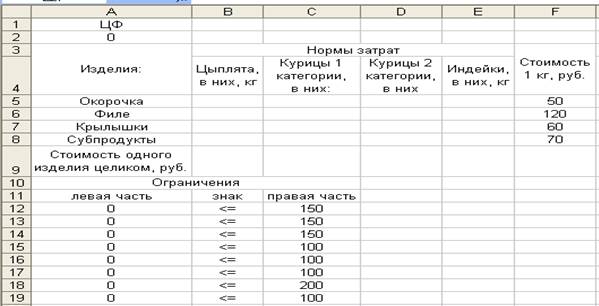
Рис. 1. Расположение исходных данных на листе MS Excel

На рис. 2 изображен лист с формулами для расчетов.

Так как формула целевой функции большая, приведем ее отдельно =(0,2*B5+0,3*C5+0,4*D5+0,9*E5)*50+(0,3*B6+0,35*C6+0,45*D6+0,8*E6)*120+ (0,1*B7+0,2*C7+0,3*D7+0,6*E7)*60+(0,05*B8+0,1*C8+0,2*D8+0,3*E8)*70+38*B9+59*C9+89*D9+180*E9.

Для получения формул в меню Сервис выбираем Параметры, ставим флажок Формулы.

                                                                                                                    

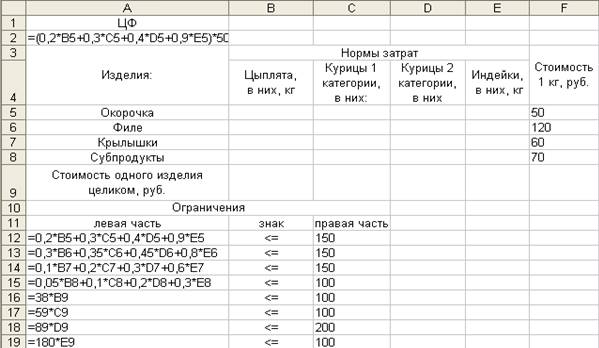
Рис. 2. Лист MS Excel в режиме отображения формул

2.Запускаем команду Поиск решения.

– Устанавливаем целевую ячейку ($А$2).

– Вводим тип целевой функции. В задаче она равна максимальному значению.

– Помещаем курсор в строку Изменяя ячейки. Вводим адреса искомых переменных $В$5:$Е$9.

– Вводим ограничения:

– в строке Ссылка на ячейку вводим адрес $A$12:$A$19, в поле Знак вводим <=, в строке Ограничение введем адрес $C$12:$C$19;

– нажмем кнопку Добавить. В появившемся окне Добавление ограничения введем остальные ограничения;

– Нажимаем ОК. На экране появляется диалоговое окно Поиск решения с введенными условиями (рис. 3).

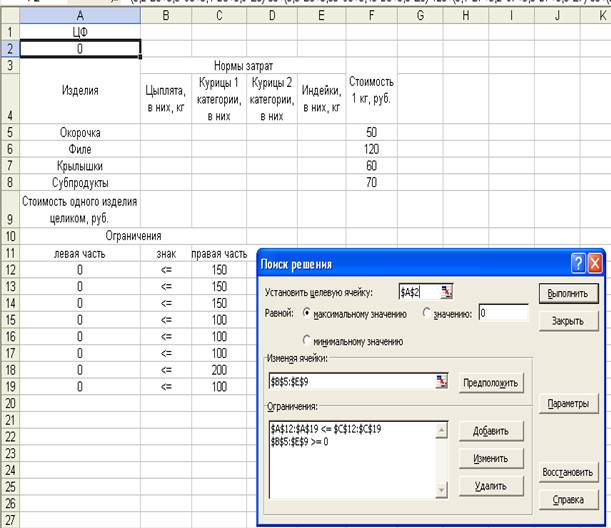
Рис. 3. Введены все условия задачи

Введем параметры в диалоговом окне Параметры поиска решения:

– Установим флажки в окнах Линейная модель и Неотрицательные значения;

– Нажимаем ОК, появляется окно Поиск решения;

– Нажимаем кнопку Выполнить.

На экране появляется диалоговое окно Результаты поиска решения, где указываем типы отчетов: по результатам, устойчивости, пределам и появляется  исходная таблица с заполненными ячейками В5:Е9 для значений Х, и ячейка А2 с максимальным значением целевой функции (рис. 4).

Получим оптимальный план: окорочка из индейки – 166,7 кг, филе из индейки – 187,5 кг, крылышки из индейки – 250 кг, субпродукты из индейки – 333,3, цыплята - 2,6 кг, курицы 1 категории – 1,7 кг, курицы 2 категории – 2,2 кг, индейки – 0,6 кг. Целевая функция (максимальная стоимость всей продукции) равна 42000 рублей.

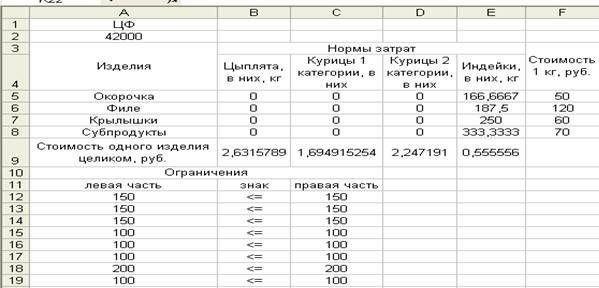
Рис. 4. Получен оптимальный план

Так как объемы спроса ограничены, то оптимальный план несколько подкорректируем и составим оптимальный ассортимент продукции (рис. 5).

Ассортимент, кг

Окорочка из индейки

Филе из индейки

Крылышки из индейки

Субпродукты из индейки

Цыплята

Курицы 1 категории

Курицы 2 категории

Индейки

150

150

150

100

100

100

200

100

Рис. 5. Оптимальный ассортимент

Отчет по результатам

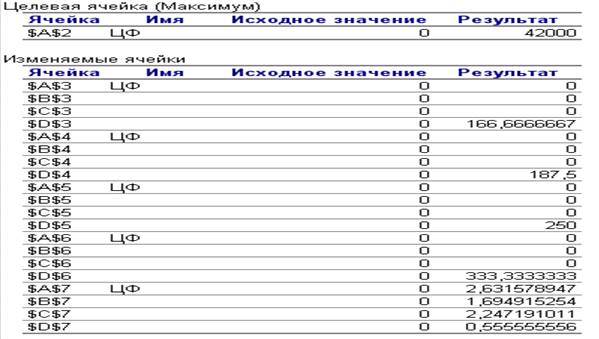
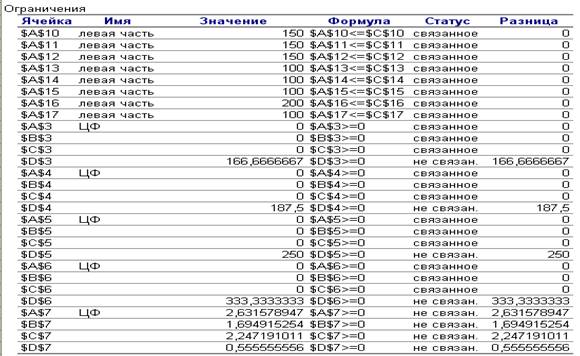
Рис. 6. Отчет по результатам

В отчете по результатам содержатся оптимальные значения переменных Х; значения целевой функции и левые части ограничений.

Отчет по устойчивости приводится на рис. 7.

Первая часть таблицы содержит информацию, относящуюся к переменным:

– Результаты решения задачи.

– Нормированная стоимость, которая показывает, насколько изменится значение ЦФ в случае принудительного включения единицы этой продукции в оптимальное решение. В данной задаче нормированная стоимость равна нулю.

– Коэффициенты целевой функции.

– Предельные значения целевых коэффициентов, при которых сохраняется первоначальное оптимальное решение. Например, допустимое увеличение цены на окорочка из индейки практически не ограничено, а допустимое уменьшение равно нулю. Это означает, что если цена уменьшится, то оптимальное решение изменится.

Во второй части содержится информация, относящаяся к ограничениям:

– Величина использованных ресурсов в колонке Результ. Значение.

– Предельные значения приращения ресурсов. В графе Допустимое уменьшение показано, насколько можно уменьшить (устранить излишек) или увеличить ресурс, сохранив при этом оптимальное решение. Например, для окорочков допустимое увеличение не ограничено, а допустимое уменьшение имеет смысл не более, чем на 150 кг.

– Теневая цена показывает, насколько изменится ЦФ при изменении запаса ресурсов на одну единицу. Ценность дополнительной единицы продукции («теневая цена») рассчитывается только для дефицитных ресурсов. В данной задаче дефицитными, то есть сдерживающими рост ЦФ, являются  все ресурсы. Они полностью используются в оптимальном плане.

Отчет по устойчивости

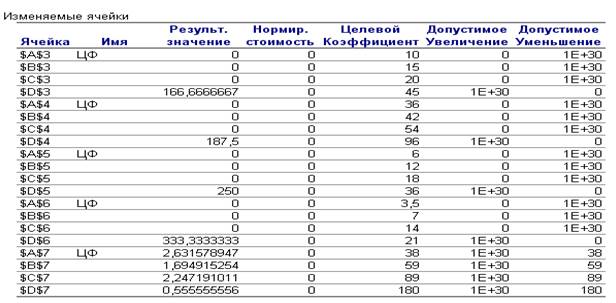
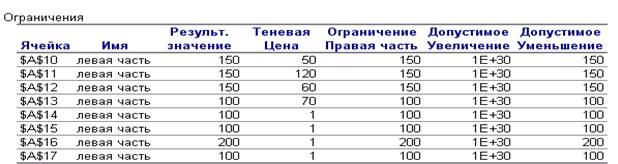
Рис. 7. Отчет по устойчивости

В отчете по пределам (рис.8) указаны значения ЦФ на верхних и нижних  пределах значений переменных Х.

Отчет по пределам

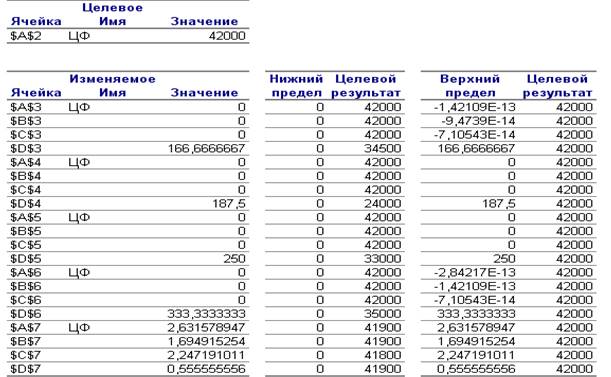
Рис. 8. Отчет по пределам

Задача 2.3.

Компания, занимающаяся ремонтом автомобильных дорог, в следующем месяце будет проводить ремонтные работы на пяти участках автодорог. Песок на участки ремонтных работ может доставляться из трех карьеров, месячные объемы предложений по карьерам известны. Из планов производства ремонтных работ известны месячные объемы потребностей по участкам работ. Имеются экономические оценки транспортных затрат (в у.е.) на перевозку 1 тонны песку с карьеров на ремонтные участки.

Числовые данные для решения содержатся ниже в матрице планирования.

Требуется:

1. Предложить план перевозок песка на участки ремонта автодорог, который обеспечивает минимальные совокупные транспортные издержки.

2. Определить, что произойдет с оптимальным планом, если изменятся условия перевозок: а) появится запрет на перевозки от первого карьера до второго участка работ; б) по этой коммуникации будет ограничен объем перевозок 3 тоннами.

Матрица планирования

Участок

работ

Карьер               

В1

В2

В3

В4

В5

Предложение

А1

4

2

3

4

1

60

А2

2

4

3

5

6

90

А3

6

5

4

6

2

140

Потребности

40

30

90

80

50

Решение

I.                         Так как целевая функция и неравенства-ограничения линейны, эта задача является задачей линейного программирования. Для ее решения применимы специальные методы, используемые для решения транспортных задач. Данная задача является транспортной задачей закрытого типа, так как суммарные запасы равны суммарным потребностям, то есть 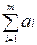  = 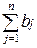 = 290.

Экономико-математическая модель задачи

Переменные: хij (i=1,2,3; j=1,2,3,4,5) – количество песка, поставляемое i-м карьером в j-й участок дорог.

Целевая функция – совокупные транспортные издержки, которые необходимо минимизировать: f(x) = 4x11 + 2x12 + 3x13 + 4х14 + х15 + 2х21 + 4х22 + 3х23 + 5х24+ +6х25+ 6х31 +5х32+4х33+6х34+2х35 → min.

Функциональные ограничения:

· по поставщикам

 х11 + х12+ х13  +х14 + х15 = 60,

х21 + х22 + х23 + х24 + х25 = 90,

х31 + х32 + х33 + х34 + х35 = 140;

· по потребителям

x11 + x21 + x314 = 40,

x12 + x22 + x32 = 30,

x13 + x23 + x33 = 90,

x14 + x24  +x34 = 80,

x15 + x25 + x35 = 50.

Прямые ограничения: xij ≥ 0.

1. Создание матрицы перевозок.

 Для этого выполним резервирование изменяемых ячеек, поэтому в блок ячеек В7:F9 введем «0» - так резервируется место, где после решения задачи будет находиться распределение поставок, обеспечивающее минимальные затраты на перевозку песка.

2. Ввод исходных данных.

В данном примере осуществим ввод мощностей трех поставщиков (карьеров) (ячейки G2:G4), потребности участков в их продукции (B5:F5), а также удельные затраты по доставке песка от конкретного поставщика к потребителю (блок B2:F4) (рис. 1).

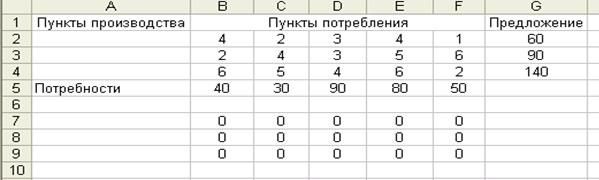
Рис. 1. Создание формы для ввода условий задачи. Ввод исходных данных и граничных условий. Изменяемые ячейки – B7:F9. В эти ячейки будет записан оптимальный план перевозок – хij.

3. Ввод граничных условий

3.1. Вводим условия реализации мощностей поставщиков

ai = ,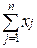

где аi – мощность поставщика i;

     xij­ – объем поставки песка от поставщика i к потребителю j;

     n - количество потребителей.

Для этого необходимо выполнить следующие операции:

·              поместить курсор в ячейку G7;

·              выбрать знак ∑;

·              выделить необходимые для суммирования ячейки B7:F7;

·              нажать ENTER для подтверждения ввода формулы для суммирования.

·              поместить курсор в ячейку G7 и скопировать в буфер введенную в нее формулу;

·              выделить ячейки G8:G9;

·              выбрать команду Вставить, тем самым из буфера будет вставлена формула для суммирования в G8:G9.

3.2. Вводим условия удовлетворения запросов потребителей, т.е. bj = ,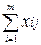

 где   bi – мощность потребителя j;

 m – количество поставщиков.

Для этого необходимо выполнить следующие операции:

·              поместить курсор в ячейку В10;

·              выбрать знак ∑, при этом автоматически выделяется столбец В7:В9;

·              нажать ENTER для подтверждения суммирования показателей выделенного столбца.

Аналогичные действия выполним для ячеек С10:F10.

Таким образом, введены ограничения для всех поставщиков и всех потребителей.

4. Назначение целевой функции.

Для вычисления значения целевой функции, соответствующей минимальным суммарным затратам на доставку песка, необходимо зарезервировать ячейку и ввести формулу для ее вычисления

F =,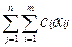

где cij – стоимость доставки единицы песка от поставщика i к потребителю j;

       xij­ – объем поставки песка от поставщика i к потребителю j.

Для этого необходимо произвести следующие действия:

·              поместить курсор в ячейку G10 (после решения задачи в данной ячейке будет находиться значение целевой функции);

·              запустить Мастер функций (значок fx);

·              в окне Категория выбрать Математические;

·              в окне Функция выбрать СУММПРОИЗВ;

·              нажать кнопку ОК;

·              в окне СУММПРОИЗВ указать адреса массивов, элементы которых обрабатываются этой функцией.

В задаче целевая функция представляет собой произведение удельных затрат на доставку груза (расположенных в блоке ячеек B2:F4) и объемов поставок для каждого потребителя (содержимое ячеек B7:F9). Для этого надо:

·              в поле Массив 1 указать адреса B2:F4; в поле Массив 2 указать адреса B7:F9;

·              нажать кнопку ОК. На рис. 2 представлено решение задачи в формульном виде.

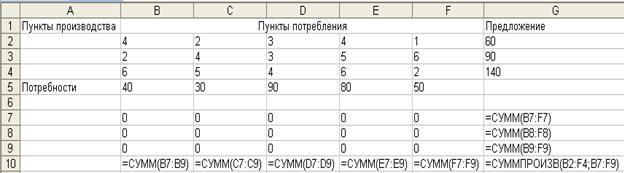
Рис. 2. Формульный вид задачи

 5. Ввод зависимостей из математической модели.

Для этого необходимо выполнить следующие действия:

·              выбрать Сервис → Поиск решения;

·              поместить курсор в поле Установить целевую ячейку;

·              ввести адрес ячейки $G$10;

·              ввести тип целевой функции, равный минимальному значению;

·              ввести адреса изменяемых ячеек B7:F9. Для этого необходимо:

·              выбрать Изменяя ячейки;

·              ввести адреса $В$7:$F$9.

6. Ввод ограничений задачи.

В матрицу перевозок, содержащую исходные данные по задаче, необходимо ввести условие реализации мощностей всех поставщиков. Для этого необходимо:

·               выбрать Добавить ограничения;

·               в поле Ссылка на ячейку ввести адреса $G$7:$G$9;

·               в поле Знак установить знак «=».

·               в поле Ограничение установить адреса $G$2:$G$4;

Ввести ограничение, реализующее условие удовлетворения мощностей всех потребителей: выбрать Добавить ограничения;

·               в поле Ссылка на ячейку ввести адреса $В$10:$F$10;

·               в поле Знак выбрать знак «=»;

·               в поле Ограничение установить адреса $B$5:$F$5;

·               нажать кнопку ОК. На экране появится окно Поиск решения с введенными ограничениями (рис. 3).

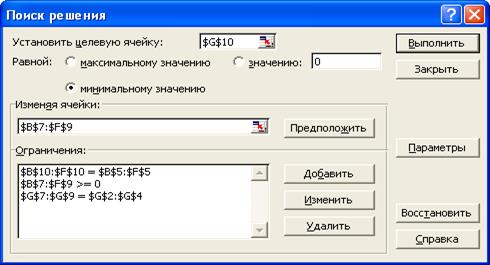
            Рис. 3. Ввод зависимостей из математической модели

7. Ввод параметров (рис. 4).

С помощью окна Параметры можно вводить условия для решения оптимизационных задач. В данной задаче установим флажок Неотрицательные значения.

·              нажмем кнопку ОК. Опять появится диалоговое окно Поиск решения.

·              Нажмем кнопку Выполнить. В результате на экране появится диалоговое окно Результаты поиска решения (рис. 5).

                     

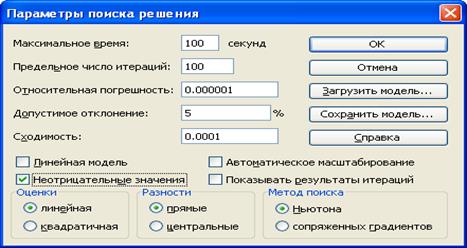
Pис. 4. Параметры Поиска решения

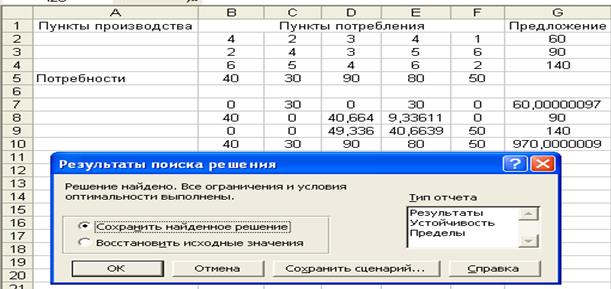
Рис. 5. Результаты поиска решения

Получен оптимальный план перевозок:

х12 = 30 ед. груза следует перевезти из карьера 1 на участок 2;

х14 = 30 ед. груза следует перевезти из карьера 1 на участок 4;

х21 = 40 ед. груза следует перевезти из карьера 2 на участок 1;

х23 = 40,7 ед. груза следует перевезти из карьера 2 на участок 3;

х24 = 9,3 ед. груза следует перевезти из карьера 2 на участок 4;

х33 = 49,3 груза следует перевезти из карьера 3 на участок 3;

х34 = 40,7 груза следует перевезти из карьера 3 на участок 4;

х35 = 50 груза следует перевезти из карьера 3 на участок 5.

Общая стоимость транспортных затрат равна 970 у.е.

Отчет по результатам приведен на рис. 6.

Отчет по результатам

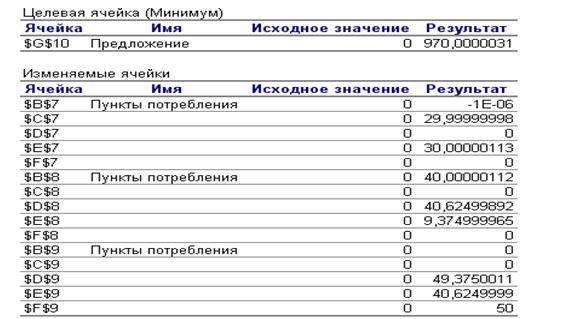
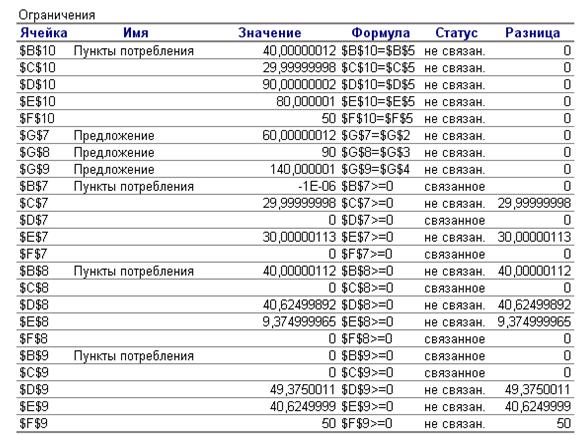
Рис. 6. Отчет по результатам

Рекомендации лицу, ответственному за принятие решений: работая по такому оптимальному плану все ресурсы поставщиков, будут израсходованы и доставлены потребителям.

II. а) Если появится запрет на перевозки от первого карьера до второго участка работ, то вместо значения х12 = 2(ячейка С2) введем значение х12 = 1000. Получим новую матрицу с введенными условиями (рис. 7).

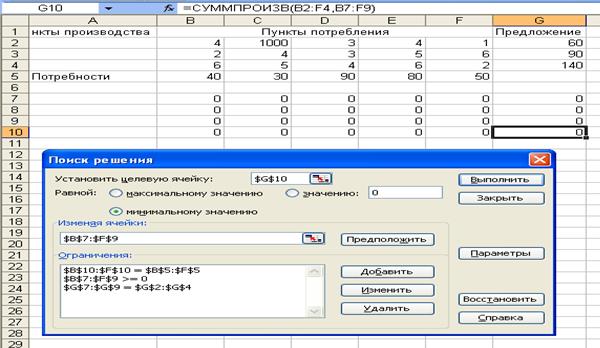
Рис. 7. Матрица с запретом на значение х12

 

Полученный новый оптимальный план представлен на рис. 8

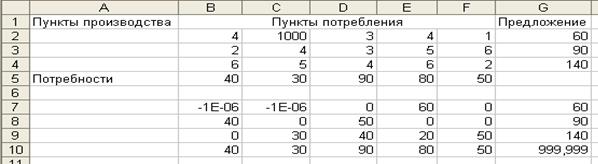
Рис. 8. а) Новый оптимальный план

При этом целевая функция (транспортные затраты) увеличилась с 970 до 999,999 у.е. и оптимальный план изменился таким образом:

        х11 = 0 ед. груза следует перевезти из карьера 1 на участок 1;

        х12 = 0 ед. груза следует перевезти из карьера 1 на участок 2;

х14 = 60 ед. груза следует перевезти из карьера 1 на участок 4;

х21 = 40 ед. груза следует перевезти из карьера 2 на участок 1;

х23 = 50 ед. груза следует перевезти из карьера 2 на участок 3;

х32 = 30 ед. груза следует перевезти из карьера 3 на участок 2;

х33 = 40 ед. груза следует перевезти из карьера 3 на участок 3;

х34 = 20 ед. груза следует перевезти из карьера 3 на участок 4;

х35 = 50 ед. груза следует перевезти из карьера 3 на участок 5.

б) Если объем перевозок от первого карьера до второго участка работ будет ограничен 3 тоннами, то есть к исходным условиям добавим еще дополнительное ограничение: $C$7 ≤ 3 (рис. 9).

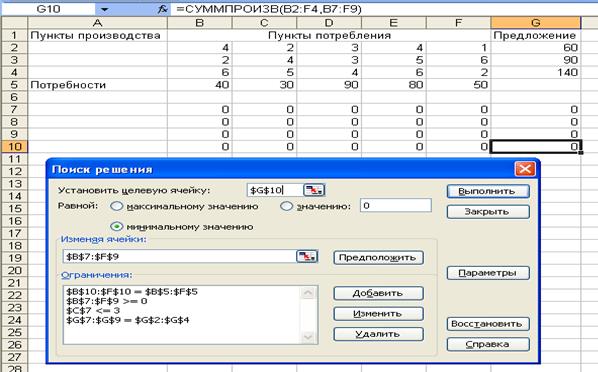
Рис. 9. Условия задачи с дополнительным ограничением $C$7 <= 3

Полученный оптимальный план представлен на рис. 10.

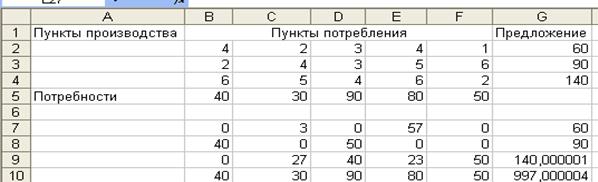
Рис. 10. б) Новый оптимальный план

Целевая функция (стоимость перевозок) увеличилась с 970 до 997 у.е.

Оптимальный план изменился так:

х12 = 3 ед. груза следует перевезти из карьера 1 на участок 2;

х14 = 57 ед. груза следует перевезти из карьера 1 на участок 4;

х21 = 40 ед. груза следует перевезти из карьера 2 на участок 1;

х23 = 50 ед. груза следует перевезти из карьера 2 на участок 3;

х32 = 27 ед. груза следует перевезти из карьера 3 на участок 2;

х33 = 40 ед. груза следует перевезти из карьера 3 на участок 3;

х34 = 23 ед. груза следует перевезти из карьера 3 на участок 4;

х35 = 50 ед. груза следует перевезти из карьера 3 на участок 5.