1. Сущность средних величин и правила их применения

Средняя величина - это обобщающая количественная характеристика совокупности однотипных явлений по одному варьирующему признаку. В экономической практике используется широкий круг показателей, вычисленных в виде средних величин.

  Например, обобщающим показателем доходов рабочих акционерного общества (АО) служит средний доход одного рабочего, определяемый отношением фонда заработной платы и выплат социального характера за рассматриваемый период (год, квартал, месяц) к численности рабочих АО. Для лиц с достаточно однородным уровнем доходов, например, работников бюджетной сферы и пенсионеров по старости (исключая имеющих льготы и дополнительные доходы) можно определить типичные доли расходов на покупку предметов питания. Так можно говорить о средней продолжительности рабочего дня, среднем тарифном разряде рабочих, среднем уровне производительности труда и т.д.

Важнейшее свойство средней величины заключается в том, что она представляет значение определенного признака во всей совокупности одним числом, несмотря на количественные различия его у отдельных единиц совокупности, и выражает то общее, что присуще всем единицам изучаемой совокупности. Таким образом, через характеристику единицы совокупности она характеризует всю совокупность в целом.

Средние величины связаны с законом больших чисел. Суть этой связи заключается в том, что при осреднении случайные отклонения индивидуальных величин в силу действия закона больших чисел взаимопогашаются и в средней выявляется основная  тенденция развития, необходимость, закономерность, однако, для этого среднюю необходимо вычислять на основе обобщения массы фактов.

Средние величины позволяют сравнивать показатели, относящиеся к совокупностям с различной численностью единиц. Важнейшим условием научного использования средних величин в статистическом анализе общественных явлений является однородность совокупности, для которой исчисляется средняя. Одинаковая по форме и технике вычисления  средняя в одних условиях  (для неоднородной совокупности) фиктивная, а в других (для однородной совокупности) соответствует действительности. 

Качественная однородность совокупности определяется на основе всестороннего теоретического анализа сущности явления. Так, например, при исчислении средней урожайности требуется, чтобы исходные данные относились к одной и той же культуре (средняя урожайность пшеницы) или группе культур (средняя урожайность зерновых). Нельзя вычислять среднюю для разнородных культур. Средние, полученные для неоднородных совокупностей, будут искажать характер изучаемого общественного явления, фальсифицировать его, или будут бессмысленными. Так, если рассчитать средний уровень доходов служащих какого-либо района, то получится фиктивный средний показатель, поскольку для его исчисления использована неоднородная совокупность, включающая в себя служащих предприятий различных типов (государственных, совместных, арендных, акционерных), а также органов государственного управления, сферы науки, культуры, образования и т.п. В таких случаях метод средних используется в сочетании с методом группировок, позволяющим выделить однородные группы, по которым и исчисляются типические групповые средние. Средине величины очень тесно связаны с методом группировок, т.к. для характеристики явлений необходимо исчислять не только общие (для всего явления) средние, но и групповые (для типических групп этого явления по изучаемому признаку).

Групповые средние позволяют избежать "огульных" средних, обеспечивают сравнение уровней отдельных групп с общим уровнем по совокупности, выявление имеющихся различий и т.д.

Однако нельзя сводить роль средних только к характеристике типических значений признаков в однородных по данному признаку совокупностях. На практике современная статистика использует так называемые системные средние, обобщающие неоднородные явления (характеристики государства, единой народнохозяйственной системы: например, средний национальный доход на душу населения, средняя урожайность зерновых по всей стране, средний реальный доход на душу населения, среднее потребление продуктов питания на душу населения, производительность общественного труда).[1]

В современных условиях развития рыночных отношений в экономике средние служат инструментом изучения объективных закономерностей социально-экономических явлений. Однако в экономическом анализе нельзя ограничиваться лишь средними показателями, так как за общими благоприятными средними могут скрываться и крупные серьезные недостатки в деятельности отдельных хозяйствующих субъектов, и ростки нового, прогрессивного. Так, например, распределение населения по доходу позволяет выявлять формирование новых социальных групп. Поэтому наряду со средними статистическими данными необходимо учитывать особенности отдельных единиц совокупности.

Средняя величина может принимать такие значения, которые не присущи непосредственно ни одному из элементов изучаемой совокупности, кроме того, на практике часто средняя величина для дискретного признака выражается как для непрерывного. Например, среднее число родившихся на каждую тысячу населения в регионе: в регионе имеются несколько населенных пунктов, в каждом из которых складывается собственный уровень рождаемости. Чтобы рассчитать среднюю рождаемость по региону необходимо численность всех родившихся младенцев соотнести с численностью населения и умножить на 1000:

Результат расчета средней величины по данному показателю может выражаться в дробных числах, несмотря на то, что показатель «число родившихся» является целым числом.

Средняя величина являются равнодействующей всех факторов, оказывающих влияние на изучаемое явление. То есть, при расчете средних величин взаимопогашаются влияние случайных (пертурбационных, индивидуальных) факторов и, таким образом, возможно определение закономерности, присущей исследуемому явлению.

Математические приемы, используемые в различных разделах статистики, непосредственно связаны с вычислением средних величин.

Средние в общественных явлениях обладают относительным постоянством, т.е. в течение какого-то определенного промежутка времени однотипные явления характеризуются примерно одинаковыми средними.[2]

Условия применения средних величин в анализе

Как уже говорилось выше обязательным условием расчета средних величин для исследуемой совокупности является ее однородность. Действительно, допустим, что отдельные элементы совокупности, вследствие подверженности влиянию некоторого случайного фактора, имеют слишком большие (или слишком малые) величины изучаемого признака, существенно отличающиеся от остальных. Такие элементы повлияют на размер средней для данной совокупности, поэтому средняя не будет выражать наиболее характерную для совокупности величину признака.

Если исследуемое явление не является однородным, то его разбивают на группы, содержащие только однородные элементы. Для такого явления рассчитываются сначала средние по группам, которые называются групповые средние, – они будут выражать наиболее типичную величину явления в каждой группе. Затем рассчитывается для всех элементов общая средняя величина, характеризующая явление в целом, – она рассчитывается как средняя из групповых средних, взвешенных по числу элементов совокупности, включенных в каждую группу. На практике, однако, безусловное выполнение данного условия повлекло бы за собой ограничение возможностей статистического анализа общественных процессов. Поэтому, часто средние величины рассчитываются по неоднородным явлениям. Например, при расчете величины средней заработной платы по Тюменской области, когда совместно анализируется заработная плата труда в автономных округах и в южных районах Тюменской области, а затем полученный средний уровень заработной платы труда сопоставляется с соседними сибирскими регионами.

Еще одним важным условием применения средних величин в анализе является достаточное количество единиц в совокупности, по которой рассчитывается среднее значение признака. Достаточность анализируемых единиц обеспечивается корректным определением границ исследуемой совокупности, т.е. закладывается еще на начальном этапе статистического исследования. Данное условие становится решающим при применении выборочного наблюдения, когда необходимо обеспечить репрезентативность выборки.

Определение максимального и минимального значения признака в изучаемой совокупности также является условием применения средней величины в анализе. В случае больших отклонений между крайними значениями и средней, необходимо проверить принадлежность экстремумов к исследуемой совокупности. Если сильная изменчивость признака вызвана случайными, кратковременными факторами, то, возможно, крайние значения не характерны для совокупности. Следовательно, их следует исключить из анализа, т.к. они оказывают влияние на размер средней величины.

В статистике выделяют несколько видов средних величин:

1. По наличию признака-веса:

-                       невзвешенная средняя величина;

-                       взвешенная средняя величина.

2. По форме расчета:

-                       средняя арифметическая величина;

-                       средняя гармоническая величина;

-                       средняя геометрическая величина;

-                       средняя квадратическая, кубическая и т.д. величины.

3. По охвату совокупности:

-                       групповая средняя величина;

-                       общая средняя величина.

Средние величины различаются в зависимости от учета признаков, влияющих на осредняемую величину:

Если средняя величина рассчитывается для признака, без учета влияния на него каких-либо других признаков, то такая средняя величина называется средней невзвешенной или простой средней.

Если имеются сведения о влиянии на осредняемый признак некоторого признака или нескольких признаков, которые необходимо учесть при расчете для корректного расчета средней величины, то рассчитывается средняя взвешенная.[3]

2. Множественная корреляция

Множественная корреляция - корреляция между одной зависимой переменной и комбинацией двух или более независимых переменных, которая дает оценку смешанного влияния на зависимую переменную.

Корреляционная связь - это связь, при которой определенному значению факторного признака соответствует лишь среднее значение результативного признака.

Существуют также связи непосредственные и косвенные. Фактор X может непосредственно оказывать влияние на Y или косвенно, через другой фактор W.

Связь между двумя признаками (результативным и факторным или двумя факторными) называется парной корреляцией.

Зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков - это частная корреляция.

Зависимость же результативного и двух или более факторных признаков, включенных в исследование, называется множественной корреляцией.

Корреляционный анализ имеет своей задачей количественное определение тесноты связи между признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи). Теснота связи количественно выражается величиной коэффициентов корреляции.

Регрессивный анализ заключается в определении аналитического выражения связи, в котором изменение результативного признака обуславливается влиянием одного или нескольких факторных признаков, а множество всех прочих факторов применяется за постоянные (или усредненные) величины.

Корреляционно-регрессивный анализ включает в себя измерение тесноты и направления связи, а также установление аналитического выражения (формы) связи.

Если число переменных, от которых зависит выходная величина, больше чем одна, речь идет о множественных регрессии и корреляции. В общем случае число переменных n  и мы имеем дело с n – мерным распределением переменных

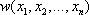
Запишем центральные моменты второго порядка для этого распределения

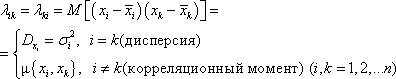
 Эти моменты определяют матрицу моментов 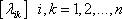. Определитель этой матрицы 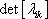   называется обобщенной дисперсией n – мерного распределения. Коэффициентами корреляции распределения называются величины

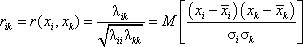
Эти коэффициенты определяют корреляционную матрицу 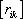, если все 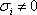. Регрессия величины  на остальные 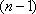  переменные часто аппроксимируется функцией линейной регрессии 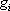. В этом случае имеет место соотношение

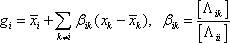
Здесь 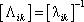 - матрица, обратная матрице моментов.

В качестве меры корреляции между 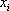 и остальными  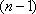величинами используется сводный коэффициент корреляции, который определяется соотношением

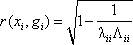
Коэффициентный анализ при множественной корреляции

Для оценки тесноты множественных корреляционных связей применяются линейный коэффициент множественной корреляции и теоретическое множественное корреляционное отношение.

Линейный коэффициент множественной корреляции применителен к двухфакторным моделям:

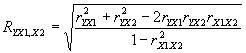
Теоретическое множественное корреляционное отношение, называемое также совокупным индексом корреляции, выражается через дисперсию:

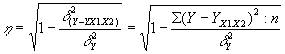
где d 2(y-yx1x2) – остаточная дисперсия;

d 2y – дисперсия результативного признака.

Ryx1x2 и h варьируются в тех же пределах и имеют тот же смысл, что и в парной корреляции:

а) их квадраты – коэффициент множественной детерминации – это доли учтенных факторов в общей сумме факторов;

б) линейный коэффициент множественной корреляции показывает только прямолинейную связь, а теоретическое множественное корреляционное отношение – любую связь.

Наконец совокупный множественный индекс корреляции в общем виде определяется по формуле:

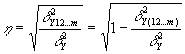
где d 2Y12…m – факторная дисперсия;

d 2Y – дисперсия результативного признака;

d 2Y(12…m) – остаточная дисперсия.

Кроме линейного коэффициента множественной корреляции (Ryx1x2…хm), совокупного коэффициента множественной корреляции (h ) и ранее исчисляемых коэффициентов парной корреляции (ryxj), рассчитывают также частные коэффициенты корреляции и частные коэффициенты эластичности.

Частный коэффициент корреляции – это показатель, характеризующий тесноту связи между признаками при элиминировании влияния всех остальных признаков:

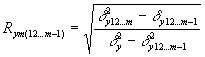
где d 2y12…m – дисперсия результативного признака;

d 2y12…m-1 – остаточная дисперсия y на x1, x2,…, xm-1;

d 2y – факторная дисперсия y на x1, x2,…, xm.

Частный коэффициент эластичности показывает, на сколько процентов измениться результативный признак при изменении соответствующего факторного признака на 1% (при фиксированном значении остальных факторов на среднем уровне):

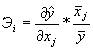
где частная производная от регрессии по переменной xj:

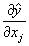 среднее значение фактора xj и результативного признака y 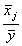 .[4]

Задача 1

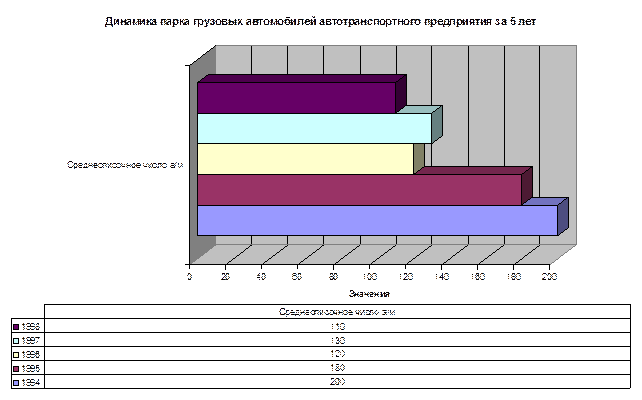
Имеются данные, характеризующие динамику парка грузовых автомобилей автотранспортного предприятия за 5 лет:

Изобразите приведенные в таблице данные при помощи столбиковой линейной диаграммы.

Решение:

Для построения столбиковой линейной диаграммы воспользуемся программой Excel.

Задача 2

Выявить основную тенденцию по объемам перевозок способом укрупнения  интервалов, рассчитав переменные средние. За укрупненный интервал принять квартал. Результат оформить в таблице

Решение:

Для решения задачи найдем переменные средние величины квартала (трех месяцев) и запишем данные в таблицу.

I квартал – (400+380+440)/3 = 406,667

II квартал – (460+480+490)/3 = 476,667

II квартал – (500+490+510)/3 = 500

II квартал – (520+500+480)/3 = 500. [5]

Список литературы        

1.          Боярский А.Я., Громыко Г.Л. Общая теория статистики. - М.: ЮНИТИ, 2003.

2.          Гусаров В.М. Теория статистики. - М.: Логос, 2004.

3.          Елисеева И.И. Эконометрика. – М.: Финансы и статистика, 2002.

4.          Общая теория статистики./Под ред. Аверченко А. П. – М.: ИНФРА-ДАНА, 2002.

5.          Статистика./Под ред. Лазарева Р. О. –  Ростов-на-Дону, 2004.

[1] Боярский А.Я., Громыко Г.Л. Общая теория статистики. - М.: ЮНИТИ, 2003. – С. 173

[2] Статистика./Под ред. Лазарева Р. О. – Ростов-на-Дону, 2004. – С. 218

[3] Гусаров В.М. Теория статистики. - М.: Логос, 2004. – С. 286

[4] Общая теория статистики./Под ред. Аверченко А. П. – М.: ИНФРА-ДАНА, 2002. – С. 160

[5] Елисеева И.И. Эконометрика. – М.: Финансы и статистика, 2002. – С. 105