СОДЕРЖАНИЕ

СОДЕРЖАНИЕ.. 2

1. СУЩНОСТЬ СРЕДНИХ ВЕЛИЧИН И ПРАВИЛА ИХ ПРИМЕНЕНИЯ.. 3

2. МНОЖЕСТВЕННАЯ КОРРЕЛЯЦИЯ.. 8

ЗАДАЧА 1. 12

ЗАДАЧА 2. 13

СПИСОК ЛИТЕРАТУРЫ... 16

1. СУЩНОСТЬ СРЕДНИХ ВЕЛИЧИН И ПРАВИЛА ИХ ПРИМЕНЕНИЯ

В процессе обработки и обобщения статистических данных возникает необходимость определения средних величин. Как правило, индивидуальные значения одного и того же признака у различных единиц совокупности неодинаковы.

Средней величиной называется обобщенная характеристика совокупности однотипных явлений по количественно-варьирующему признаку, который отображает объективный уровень признака, отнесенный к единице совокупности в конкретных условиях места и времени.[1]

Сущность средних величин заключается в следующем: в средних величинах взаимопогашаются отклонения значений признака, которые  обусловлены действием случайных факторов и  учитываются изменения, вызванные действием основных факторов.

Особенностями средних величин являются:

− средняя величина погашает случайность  и проявляет закономерность;

− средняя величина не совпадает с индивидуальными значениями признака;

− средняя величина реальная, отображает объективное свойство явления;

− средняя величина характеризует всю совокупность в целом, но задается на единице этой совокупности;

− средняя величина – относительно устойчивая величина, следовательно,  можно сравнивать среднюю величину во времени, следовательно,  средняя величина  − главный показатель экономического анализа.

Чтобы средняя величина точно отражала типичный уровень явлений, нужно соблюдать основные требования ее расчета: средняя величина должна рассчитываться только для качественно однородной совокупности.

При нарушении этого  требования получается фиктивная средняя. Чтобы этого не было средняя величина должна рассчитываться на основе метода группировки.

При расчете средней величины погашаются наименьшие и наибольшие величины, скрывается прогрессивное и отсталое, нельзя проследить за динамикой изучаемого процесса.

Средняя, рассчитанная по совокупности в целом, называется общей средней, средние, исчисленные для каждой группы, − групповыми средними. Общая средняя отражает общие черты изучаемого явления, групповая средняя дает характеристику размера явления, складывающуюся в конкретных условиях данной группы.

Групповые средние используются для изучения закономерностей развития общественных явлений. Так, в аналитических группировках анализ групповых средних позволяет сделать вывод о наличии и направлении взаимосвязи между группировочным (факторным) признаком и результативным показателем.

Групповые средние широко применяются также при определении имеющихся неиспользованных резервов производства, когда на ряду со средними величинами рассматриваются и индивидуальные значения признака.

Существует две категории средних величин: степенные средние (к ним относится средняя арифметическая, средняя гармоническая, средняя геометрическая и другие), а также структурные средние (мода и медиана). Выбор того или иного вида средней производится в зависимости от цели исследования, экономической сущности усредняемого показателя и характера имеющихся исходных данных.

При выборе вида средней величины обычно исходят из логической сущности осредняемого признака и его взаимосвязи с итоговым  (определяющим) показателем. Величина итогового показателя не должна изменяться при замене индивидуальных значений признака средней величины.

Способность средних величин сохранять свойство статистических  совокупностей называют определяющим свойством.

Средняя арифметическая применяется, если известны значения осредняемого признака (х) и количество единиц совокупности с определенным значением признака (f).

Средняя арифметическая бывает простой и взвешенной.

Средняя арифметическая простая определяется, если индивидуальные значения признака не повторяются. Она равна отношению суммы отдельных значений признака к их числу. Средняя арифметическая простая определяется по формуле:

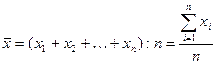                            ,                                                  (1)

где х_i – индивидуальное значение признака каждой единицы совокупности;

n – число единиц совокупности.

В статистике часто имеет дело не результат наблюдения, а результат сводки и группировки, следовательно, индивидуальное значение признака часто повторяется, и средний показатель рассчитывается по средней арифметической взвешенной. Средняя арифметическая взвешенная определяется по формуле:

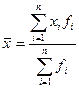                                                             ,                                                           (2)

где n – число групп;

      х – значение осредняемого признака;

      f – вес значения признака, частота.

Средняя арифметическая обладает рядом свойств:

1) От уменьшения или увеличения частот каждого значения признака х в n раз величина средней арифметической не изменится.

2) Если все частоты разделить или умножить на какое-либо число, то величина средней не изменится.

3) Общий множитель индивидуальных значений признака может быть вынесен за знак средней:

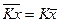
4) Средняя суммы (разности) двух или нескольких величин равна  сумме (разности) их средних:

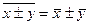
5) Если х=с, где с – постоянная величина, то .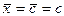

6) Сумма отклонений значений признака Х от средней арифметической х равна нулю:

                                                        

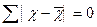
Результаты наблюдения иногда не дают возможности применить среднюю взвешенную, когда в учете отсутствуют данные о частоте появления признака, но имеется информация об общем значении признака. Когда есть эта информация, тогда средняя взвешенная преобразовывается в среднюю гармоническую.

Произведение х* f дает объем осредняемого признака х для совокупности единиц и обозначается w. Если в исходных данных имеются значения осредняемого признака х и объем осредняемого признака w, то для расчета средней применяется гармоническая взвешенная:

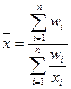                                                                                                                        (3)

где х – значение осредняемого признака х (варианта);

       w – вес варианты х, объем осредняемого признака.

Форма средней гармонической простой (невзвешенной) используется значительно реже. Она имеет следующий вид:

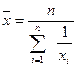                                                                                                                       (4)

где х – значение осредняемого признака;

n – число значений х.

То есть это обратная величина средней арифметической простой из обратных значений признака.

На практике средняя гармоническая простая применяется редко, в тех случаях, когда значения w для единиц совокупности равны.

Средняя хронологическая используется тогда, когда данные приведены на определенный момент времени (на конкретную дату), например на первое число месяца. Средняя хронологическая определяется по формуле:

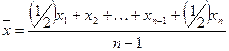                                                                                 (5)

где 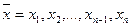 - значение осредняемого признака;

       n – число дат внутри периода, на которые заданы значения х.

По средней хронологической исчисляется среднегодовая стоимость основных фондов предприятия из данных о наличии на начало каждого месяца; средний остаток вкладов на счетах в банке по информации на начало месяца.

Если значения осредняемого признака существенно отстоят друг от друга или заданы коэффициентами (темпы роста, индексы цен), то для расчета применяют среднюю геометрическую.

 Средняя геометрическая исчисляется извлечением корня степени и из произведений отдельных значений – вариантов признака х:

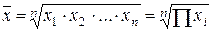                                                                                       (6)

где n – число вариантов;

П – знак произведения.

Наиболее широкое применение средняя геометрическая получила для определения средних темпов изменения в рядах динамики, а также в рядах распределения.

Структурные средние величины применяются для изучения внутреннего строения и структуры рядов распределения значения признака.

Мода (Мо) – значение признака, которое наиболее часто встречается в исследуемой совокупности.

Моду определяют по формуле:

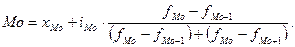                         ,                                   (7)

где 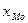 - начальное значение интервала, содержащего моду;

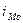        - величина модального интервала;

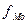        - частота модального интервала;

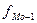        - частота интервала, предшествующего модальному;

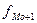        - частота интервала, следующего за  модальным.

Медиана (Ме) – значение признака, который приходится на середину упорядоченной (ранжированной) совокупности.

Медиану определяют по формуле:

                                  ,                                                      (8)

где x₀ – нижняя граница медианного интервала;

      i_Me – величина медианного интервала;

      S_me-1 – сумма накопленных частот до медианного интервала;

      f_Me  - частота медианного интервала.

Для дискретных вариационных рядов: мода – значение варианта с наибольшей частотой. Мода используется при изучении спроса на товар, регистрации цен.[2]

Для нахождения медианы нужно найти значение признака в середине ряда.

2. МНОЖЕСТВЕННАЯ КОРРЕЛЯЦИЯ

Корреляционная связь – это связь, где воздействие отдельных факторов проявляется только как тенденция (в среднем) при массовом наблюдении фактических данных.[3]  Примерами корреляционной зависимости  могут быть зависимости между размерами активов банка, ростом производительности труда и стажем работы сотрудников.

Наиболее простым вариантом корреляционной зависимости является парная корреляция, т.е. зависимость между двумя признаками (результативным и факторным или между двумя факторными). Математически эту зависимость можно выразить как зависимость результативного показателя у от факторного показателя х. Связи могут быть прямые и обратные. В первом случае с увеличением признака х увеличивается и признак у, при обратной связи с увеличением признака х уменьшается признак у.

Одновременное изучение корреляции нескольких переменных проводится на основании использования методов множественной корреляции. Так, рассматривая уровень фондоотдачи на различных предприятиях отрасли, можно установить, что величина его зависит от размеров предприятия, удельного веса активной части фондов, степени изношенности фондов, их обновления и ряда других факторов.

Рассчитав параметры уравнения множественной зависимости определяем значение индекса корреляции по следующей формуле:

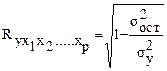                                                                                                (9)

где  ─ общая дисперсия результирующего признака;

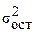 ─ остаточная дисперсия для уравнения у=f(х₁, х₂,…..х_р)

По параметрам полученного уравнения можно оценить долю каждого из факторов в изменении уровня результативного показателя у. Это может быть сделано путем прямой оценки по величине коэффициентов регрессии при каждом из факторов, а также по коэффициентам эластичности Э_хi, стандартизированным частным коэффициентам регрессии β-коэффициентам и Δ-коэффициентам.

Коэффициенты уравнения множественной регрессии показывают абсолютный размер влияния факторов на уровень результативного показателя и характеризуют степень влияния каждого фактора на анализируемый показатель при фиксированном (среднем) уровне других факторов, входящих в модель.

Для сравнения  оценок роли различных факторов в формировании моделируемого показателя следует дополнить абсолютные величины относительными. Так, частные коэффициенты эластичности показывают, на сколько процентов в среднем изменяется у с изменением признака-фактора х_i на один процент при фиксированном положении других факторов, и рассчитывается по формуле:

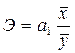                                                                                                             (10)

где   а_i  - коэффициент регрессии при i-м факторе.

β-коэффициенты показывают на какую часть среднего квадратического отклонения δ_у изменится зависимая переменная у с изменением соответствующего фактора х_i на величину своего среднеквадратического отклонения (δ_i). Это коэффициент позволяет сравнивать влияние колеблемости различных факторов на вариацию исследуемого показателя, на основе чего выявляются факторы, в развитии которых заложены наибольшие резервы изменения результативного показателя:

                                                  β_i= а_i*δ_i / δ_у                                                                         (11)

Коэффициенты эластичности и β-коэффициенты взаимосвязаны следующим образом:

                                             β_i = Э_i *v_i / v_у ,                                               (12)                                                 

где      v_i ─ коэффициент вариации i-го факторного признака;

            v_у ─ коэффициент вариации результативного признака.

Чтобы оценить долю влияния каждого фактора в суммарном влиянии факторов, включенных в уравнение регрессии, рассчитывают Δ-коэффициенты:

                                               Δ_i =r_iу* β_i / R²                                                                (13)

Коэффициент детерминации показывает в какой  мере вариация результативного признака обусловлена влиянием признаков-факторов, включенных в рассматриваемое уравнение корреляционной зависимости.[4]

Коэффициент детерминации определяется как квадрат множественного коэффициента корреляции. Его значение определяет долю (в процентах) изменений, обусловленных влиянием факторного признака, в общей изменчивости результативного признака.

Величина совокупного коэффициента корреляции изменяется в пределах от 0 до 1 и численно не может быть меньше, чем любой из образующих его парных коэффициентов корреляции. Чем ближе совокупный коэффициент корреляции к единице, тем меньше роль неучтенных в модели факторов и тем больше оснований считать, что параметры регрессионной модели отражают степень эффективности включенных в нее факторов.

Для случая зависимости результативного признака от двух факторных признаков формула совокупного коэффициента корреляции имеет вид:

                                      R = 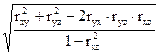,                                               (14)

где r_ij  - парные коэффициенты корреляции между соответствующими факторами.

Для более  углубленного анализа вычисляются частные коэффициенты корреляции. Частные коэффициенты (или индексы)  корреляции – характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии. Показатели частной регрессии представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.[5]

ЗАДАЧА 1

Имеются данные, характеризующие динамику парка грузовых автомобилей автотранспортного предприятия за 5 лет:

Годы	1994	1995	1996	1997	1998
Среднесписочное число а/м	200	180	120	130	110

Изобразить приведенные в таблице данные при помощи столбиковой линейной диаграммы.

Решение

Для наглядного сравнения объемов изучаемого явления во времени используются столбиковые диаграммы.

Рис. 1 Динамика парка грузовых автомобилей автотранспортного предприятия за 5 лет

ЗАДАЧА 2

Выявить основную тенденцию динамики по объему перевозок способом укрупнения интервалов, рассчитав переменные средние. За укрупненный интервал принять квартал. Результаты оформить в таблице.

Месяц	Перевезено грузов, тыс. т	Месяц	Перевезено грузов, тыс. т
Январь	400	Июль	500
Февраль	380	Август	490
Март	440	Сентябрь	510
Апрель	460	Октябрь	520
Май	480	Ноябрь	500
Июнь	490	Декабрь	480

Решение

Показатели рядов динамики позволяют определить направление и степень изменения явления за различные периоды, но иногда характер распределения не проявляется отчетливо. Необходимо предварительно обработать динамические ряды.

Одним из способов является укрупнение. При нем ряд динамики из мелких интервалов заменяют рядом из более крупных. По условию задачи за укрупненный интервал принимается квартал.

Просуммировав данные в каждом квартале, получим:

1 кв.: 400+380+440=1 220 тыс. т

2 кв.: 460+480+490=1 430 тыс. т

3 кв.: 500+490+510=1 500 тыс. т

4 кв.: 520+500+480=1 500 тыс. т.

Вычислим средние уровни ряда для укрупненных интервалов и получим среднемесячные объемы перевозок грузов по кварталам. Средний уровень ряда исчисляется как среднее арифметическое из уровней этого ряда по формуле:

                                           У_сред. =∑У _i/n,                                                       (1)

где  У _i – уровни ряда динамики;

        n – число уровней (число периодов времени).

Для характеристики средней интенсивности развития явления во времени используются динамические средние:

– средний уровень

                                           У_сред. =∑У _i/n,                                                       (2)

У_сред. =(1220+1430+1500+1500)/4=5 650/4=1 412,5 тыс. т

– средний абсолютный прирост

                                     ∆У_сред.  =У_n - У₁/ n-1                                                          (3)

∆У_сред.  =(1 500-1 220)/4-1=+93,33 тыс. т

 – средний темп роста

                                      К_рсред.=^n-1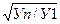                                                              (4)

где У₁, У_n – начальный и конечный уровни ряда динамики,

К_{р сред.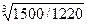} ===1,072, или 107,2%

– средний темп прироста (средняя относительная скорость изменения)

                                  К_{пр сред.} = К_{р сред.}-100                                                              (5)

К_{пр сред.}=107,2-100=+7,25%

Результаты расчетов занесем в таблицу 1

Таблица 1

Динамика объема перевозок за год по кварталам

Показатель	1 квартал	2 квартал	3 квартал	4 квартал
Среднемесячный объем перевозок грузов, тыс. т	1 220	1 430	1 500	1 500
Средний уровень ряда, тыс. т	1 412,5
Средний абсолютный прирост, тыс. т	+93,3
Средний темп роста, %	107,2
Средний темп прироста, %	+7,2

По результатам анализа среднемесячного объема перевозок за 4 квартала можно сделать следующие выводы:

Средний квартальный объем перевозок составил 1 412,5 тыс. т, при этом объем перевозок увеличивался в среднем на 93,3 тыс. т. Средний темп прироста объема перевозок составил 7,2 %.

 

 

 

 

 

 

 

 

СПИСОК ЛИТЕРАТУРЫ

1. Гусаров В.М. Теория статистики. – М.: ЮНИТИ, 1998. – 448 с.

2. Елисеева И.И., Юзбашев М.М. Общая теория статистики. – М.: Финансы и статистика, 1998. – 368 с.

3. Ефимова М. Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. – М.: ИНФРА-М. 2002. – 416 с.

4. Савицкая Г. В. Анализ хозяйственной деятельности предприятия. 2-е изд., испр. и доп. – М.: ИНФРА-М. 2003. − 400 с.

5. Теория статистики / Под редакцией Шмойловой Р. А. – М.: Финансы и статистика, 2002. – 576 с.

---

[1] Ефимова М. Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. – М.: ИНФРА-М. 2002. –с. 89

[2] Теория статистики / Под редакцией Шмойловой Р. А. – М.: Финансы и статистика, 2002. –с. 136

[3] Елисеева И.И., Юзбашев М.М. Общая теория статистики. – М.: Финансы и статистика, 1998. –с. 221

[4] Теория статистики / Под редакцией Шмойловой Р. А. – М.: Финансы и статистика, 2002. –с. 387.

[5] Ефимова М. Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. – М.: ИНФРА-М. 2002. –с. 275