Содержание

Задача 1. 3

Задача 2. 8

Задача 3. 11

Задача 4. 12

Задача 5. 16

Задача 1

Для Вашей компании существуют 4 возможных направления инвестирования капитала в размере 200 тыс. условных единиц сроком на 1 год:

1. Облигации государственного займа, по которым гарантировано 7% дохода через год.

2. Облигации газовой компании с фиксированным доходом и сроком займа на 10 лет. Однако, Ваша компания продает облигации в конце 1-го года, т.е. процент будет известен в конце года (см. таблицу).

3. Проект А, предполагающий выплаты в конце года, которые будут зависеть от состояния экономики.

4. Проект В, аналогичный проекту А, но с другим распределением выплат.

Требуется оценить ожидаемый доход и риск для всех четырех вариантов и выбрать один из них. Информация о предполагаемых доходах содержится в таблице.

Таблица 1. Норма дохода, %

Вариант инвестирования капитала	Состояние экономики и его вероятность
Спад	Застой	Неб. рост	Подъем	Бурн. рост
0,1	0,3	0,4	0,15	0,05
Облигации государственного займа	7	7	7	7	7
Облигации газовой компании	9,5	10	13,5	9	9,5
Проект А	-2,5	-1	11	11,5	15,5
Проект В	-5	-4	10	10,5	16,5

При выборе решения в качестве критериев риска используется показатель:

R = H_ij ∙ p

где р – вероятность наступления рискового события.

Предпочтение отдается решению, имеющему наименьший средневзвешенный показатель риска, определяемый как сумма произведений вероятностей различных вариантов обстановки на соответствующее им значение потерь:

R_i =∑_j=1H_ij ∙ p_j, (i=1,m)

Потери (Н_ij) рассчитываются как разность между ожидаемым результатом действия при наличии точных данных обстановки и результатом, который может быть достигнут, если данные определены:

Н_ij
(_PiOj) = max_j a_ij – a_ij

Определим для нашего задачи max_j a_ij_.

Вариант инвестирования капитала	Состояние экономики и его вероятность
Спад	Застой	Неб. рост	Подъем	Бурн. рост
0,1	0,3	0,4	0,15	0,05
Облигации государственного займа	7	7	7	7	7
Облигации газовой компании	9,5	10	13,5	9	9,5
Проект А	-2,5	-1	11	11,5	15,5
Проект В	-5	-4	10	10,5	16,5
max(aij)	9,5	10	13,5	11,5	16,5

Теперь определим величины потерь для каждого варианта инвестирования капитала и для каждого состояния экономики.

Величины потерь
Вариант инвестирования капитала	Состояние экономики и его вероятность
Спад	Застой	Неб. рост	Подъем	Бурн. рост
0,1	0,3	0,4	0,15	0,05
Облигации государственного займа	2,5	3	6,5	4,5	9,5
Облигации газовой компании	0	0	0	2,5	7
Проект А	12	11	2,5	0	1
Проект В	14,5	14	3,5	1	0

Рассчитаем показатель риска для каждого варианта решения, воспользовавшись формулой: R_i =∑_j=1H_ij ∙ p_j, (i=1,m)

Величина риска
Вариант инвестирования капитала	Состояние экономики и его вероятность
Спад	Застой	Неб. рост	Подъем	Бурн. рост
0,1	0,3	0,4	0,15	0,05
Облигации государственного займа	0,25	0,9	2,6	0,675	0,475
Облигации газовой компании	0	0	0	0,375	0,35
Проект А	1,2	3,3	1	0	0,05
Проект В	1,45	4,2	1,4	0,15	0

Общая величина риска при различных вариантах инвестирования:

Величина риска
Вариант инвестирования капитала	Состояние экономики и его вероятность	Общая величина риска
Спад	Застой	Неб. рост	Подъем	Бурн. рост
0,1	0,3	0,4	0,15	0,05
Облигации государственного займа	0,25	0,9	2,6	0,675	0,475	4,9
Облигации газовой компании	0	0	0	0,375	0,35	0,725
Проект А	1,2	3,3	1	0	0,05	5,55
Проект В	1,45	4,2	1,4	0,15	0	7,2

Таким образом, наименее рискованным является приобрести облигации газовой компании. Здесь подразумевается риск упущенной выгоды (потери).

Выбор того или иного решения зависит не только от целевых установок и ограничений, но и от склонности к риску лиц, принимающих данное решение.

Одним из классических критериев, учитывающих также и этот параметр, является критерий обобщенного максимина (пессимизма-оптимизма) Гурвица. Данный критерий, как правило, используется, если требуется остановиться между стратегией (линией поведения) в расчете на худшее и линией поведения в расчете на лучшее.

В этом случае предпочтение отдается варианту решений, для которого окажется максимальный показатель G_i, определенный по формуле:

G_i = k ∙(min_j a_ij) + (1-k)∙ (max_j a_ij)

где k – коэффициент, рассматриваемый как показатель оптимизма (0≤k≤1), при этом k=0 – линия поведения в расчете на лучшее, при k=1 – в расчете на худшее;

а_ij – выигрыш, соответствующий i-му решению при j-м варианте обстановки.

При k=1 критерий Гурвица ориентирован на осторожное поведение. При k=0 – ориентация на предельный риск, т.к. большой выигрыш, как правило, сопряжен с большим риском. Значения k между 0 и 1 являются промежуточными между риском и осторожностью и выбираются в зависимости от обстановки и склонности к риску лица, принимающего решения.

Определим критерии Гурвица для различных вариантов решений и значений коэффициента k, для этого воспользовавшись вспомогательной таблицей, в которой мы определим максимальные и минимальные значения a_ij.

Вариант инвестирования капитала	Состояние экономики и его вероятность
Спад	Застой	Неб. рост	Подъем	Бурн. рост	min_j a_ij	max_j a_ij
0,1	0,3	0,4	0,15	0,05
Облигации государственного займа	7	7	7	7	7	7	7
Облигации газовой компании	9,5	10	13,5	9	9,5	9	13,5
Проект А	-2,5	-1	11	11,5	15,5	-2,5	15,5
Проект В	-5	-4	10	10,5	16,5	-5	16,5

Определение оптимального решения с учетом критерия Гурвица

Варианты решений	Значение коэффициента Гурвица (k)
0	0,25	0,5	0,75	1
Р₁(облигации государственного займа)	7	7	7	7	7
Р₂(облигации газовой компании)	13,5	12,38	11,25	10,13	9
Р₃ (проект А)	15,5	11	6,5	2	-2,5
Р₄(проект В)	16,5	11,125	5,75	0,375	-5
Оптимальное решение	Р₄	Р₂	Р₂	Р₂	Р₂

Из данных таблицы видно, что в условиях неопределенности лицо, ориентированное на любое поведение, кроме предельного риска, выберет реализацию оптимального для него решения Р₂, и только лицо, ориентированное на предельный риск, предпочтет реализацию оптимального решения Р₄.

Выбором является решение P2.

Задача 2

Эксперты компании «ХМК» определили следующие показатели прибыли (тыс руб) в зависимости от вида стратегии и ситуации на рынке.

Стратегия компании	Ситуация 1	Ситуация 2	Ситуация 3
Выпуск холодильников	49	65	58
Выпуск морозильников	87	32	50
Выпуск кондиционеров	68	47	77

1. Стратегия при благоприятной конъюнктуре.

Если известно, что конъюнктура благоприятна – значит, можно сделать оптимистический прогноз. Воспользуемся критерием Гурвица.

Стратегия компании	Ситуация 1	Ситуация 2	Ситуация 3	Среднее	Макс	Мин
Выпуск холодильников	49	65	58	57,33333	65	49
Выпуск морозильников	87	32	50	56,33333	87	32
Выпуск кондиционеров	68	47	77	64	77	47

K=	0	0,5	1
Стратегия компании	Критерий	Критерий	Критерий
Выпуск холодильников	65	57	49
Выпуск морозильников	87	59,5	32
Выпуск кондиционеров	77	62	47

Наиболее оптимистичное решение – при к=0. Значит, наилучший стратегией будет выпуск морозильников.

2. Условия реализации неблагоприятны.

Подсчитаем некоторые статистические показатели.

Стратегия компании	Ситуация 1	Ситуация 2	Ситуация 3	Среднее	Макс	Мин	Дисперсия
Выпуск холодильников	49	65	58	57,33333	65	49	64,33333
Выпуск морозильников	87	32	50	56,33333	87	32	786,3333
Выпуск кондиционеров	68	47	77	64	77	47	237

Если условия неблагоприятны, то выбрать стоит стратегию, которая грозит минимальным риском. В данном случае это означает, что дисперсия между максимальной и минимальной прибылью должна быть минимальна, поэтому нет необходимости подсчитывать риски.

То есть, в случае неудачи – потери будут меньше и поэтому надо выпускать холодильники.

3. Существует следующий риск:

Стратегия компании	Ситуация 1	Ситуация 2	Ситуация 3
Риск	0,45	0,3	0,25
Выпуск холодильников	49	65	58
Выпуск морозильников	87	32	50
Выпуск кондиционеров	68	47	77

При выборе решения в качестве критериев риска используется показатель:

R = H_ij ∙ p

где р – вероятность наступления рискового события.

R_i =∑_j=1H_ij ∙ p_j, (i=1,m)

Н_ij
(_PiOj) = max_j a_ij – a_ij

Определим для нашего задачи max_j a_ij_.

Стратегия компании	Ситуация 1	Ситуация 2	Ситуация 3
Риск	0,45	0,3	0,25
Выпуск холодильников	49	65	58
Выпуск морозильников	87	32	50
Выпуск кондиционеров	68	47	77
max	87	65	77

Теперь определим величины потерь для каждого варианта стратегии и для каждой ситуации.

Стратегия компании	Ситуация 1	Ситуация 2	Ситуация 3
Выпуск холодильников	38	0	19
Выпуск морозильников	0	33	27
Выпуск кондиционеров	19	18	0

Величина риска:

Стратегия компании	Ситуация 1	Ситуация 2	Ситуация 3
Риск	0,45	0,3	0,25	Риск
Выпуск холодильников	17,1	0	4,75	21,85
Выпуск морозильников	0	9,9	6,75	16,65
Выпуск кондиционеров	8,55	5,4	0	13,95

Как видно, стратегией с минимальным риском является выпуск кондиционеров, при заданных вероятностях событий.

Задача 3

Выпускник школы выбирает работу. Работа сторожем гарантирует ему ежемесячный заработок 2 тыс. руб. и много свободного времени. Работа контролером в общественном транспорте обеспечивает ему заработок в зависимости от количества оштрафованных: с вероятностью 0,4 заработок составит 1,8 тыс. руб. и с вероятностью 0,6 - 3 тыс. руб. Полезность в зависимости от дохода для выпускника представлена в таблице.

Доход, тыс. руб.	1,6	1,8	1,9	2	2,1	3	3,4
Полезность, у.е.	2	3	4	6	15	21	25

Какую работу выберет выпускник, максимизирующий полезность и чему равна премия за риск?

Исходя из условия максимизации полезности, выпускник должен выбрать работу с полезностью 25 или 21 у.е. Такую полезность он получит при доходе 3 и 3,4 тыс. рублей, соответственно.

Так как работа сторожем может обеспечить только 2,0 тыс. руб. в месяц, при этом полезность равна 6 у.е., значит выпускник предпочтет работу контролером в общественном транспорте (из условия максимизации полезности). Эта работа может обеспечить ему в свою очередь только 3,4 тыс. руб. в месяц, соответственно, полезность в размере 25 у.е.

Премия за риск составляет 1 тыс. рублей (см. таблицу).

Работа	Обстановка 1	Обстановка 2	Премия^[1] / потери^[2]
(вероятность 0,4)	(вероятность 0,6)
Сторож	2	2	0 / 0
Контролер	1,8	3	1,2 / -1,2
[1][1] Если наступит обстановка 2
[1][2] Если наступит обстановка 1

Задача 4

В первых графах таблицы приведены статистические данные о финансовых инструментах А, Б и В. Проанализировать риск этих инструментов (оценить стандартное отклонение и коэффициент вариации), а также возможных портфелей, если предприниматель может выбрать одну из двух стратегий:

а) выбрать один из финансовых инструментов;

б) составить портфель, в котором 50% будет составлять один из активов и 50% - другой.

Годовые % возможных инвестиций

Год	Виды активов	Портфели
А	Б	В	АБ	БВ	АВ
(50%А+ 50%Б)	(50%В+ 50%Б)	(50%А+ 50%В)
1	9	13	23	11	18	12
2	9	11	25	10	18	13,5
3	15	17	25	16	21	14

Коэффициент вариации (ν) рассчитывается по формуле:

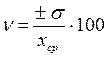
Стандартное отклонение (σ):

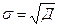
Дисперсия (Д):

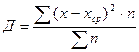
Инструмент А
Год	Норма дохода	х_ср	Д	σ	ν
1	9	11	12	3,46410162	31,4918329
2	9
3	15

Инструмент Б
Год	Норма дохода	х_ср	Д	σ	ν
1	13	13,7	9,33	3,05505046	22,3540278
2	11
3	17

Инструмент В
Год	Норма дохода	х_ср	Д	σ	ν
1	23	24,3	1,33	1,15470054	4,74534468
2	25
3	25

Инструмент АБ
Год	Норма дохода	х_ср	Д	σ	ν
1	11	12,3	10,3	3,21455025	26,063921
2	10
3	16

Инструмент БВ
Год	Норма дохода	х_ср	Д	σ	ν
1	18	19	3	1,73205081	9,11605688
2	18
3	21

Инструмент АВ
Год	Норма дохода	х_ср	Д	σ	ν
1	12	13,2	1,08	1,040833	7,90506076
2	13,5
3	14

Сгруппируем полученные данные по коэффициенту вариации, т.е. по степени риска.

Слабая вариация, низкий риск (ν до 10%)

Умеренный риск

(ν = 10 … 25%)

Высокий риск

(ν свыше 25%)

В = 4,7; БВ = 9,11; АВ = 7,9

Б=22,35

А=31,49; АБ=26

Если предприниматель должен выбрать один из финансовых инструментов А, Б, или В (стратегия а), то наименее рискованным для него будет инструмент В (коэффициент вариации 4,7%).

Если предприниматель может составить портфель из этих инструментов, то наименее рискованным является портфель АВ, включающий 50% инструмента А и 50% инструмента В.

Задача 5

В портфеле предприятия "Сибин" находятся два вида акций с разными среднегодовыми нормами доходности – акции "А" и акции "Б" с соответствующими характеристиками абсолютного размера риска в виде среднеквадратических отклонений σ (А) и σ (Б). Коэффициент корреляции текущих норм доходности акций "А" и "Б" равен: –1.

Среднегодовая норма доходности	Абсолютный размер риска
акции А	акции Б	σ_А	σ_Б
11	15,5	4,95	13,8

Найти пропорцию распределения денежных средств, инвестируемых в акции, соответствующие минимуму риска (нулевой дисперсии).

Известно, что коэффициент корреляции равен –1. Данный коэффициент рассчитывается по формуле:

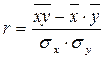, (1)

где х и y – зависимые величины. В нашем случае это нормы доходности акций А и Б, т.е.:

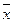= 11

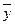= 15,5

Подставим значения этих величин в формулу коэффициента корелляции:

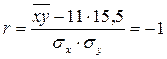
Выразим :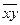

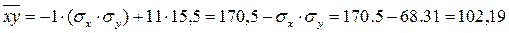
Значит средняя величина произведений норм доходности акций А и Б равна 102,19.

При распределении денежных средств, соответствующим минимуму риска, дисперсия стремится к нулю.

Выразим из формулы (1) произведение σ_А σ_Би приравняем к нулю.

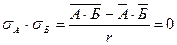
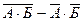= 0

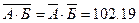
Значит распределение средств должно быть таким, чтобы произведение средних норм доходности акций было равно 102,19.