Оглавление

Задача №1. 3

Задача №2. 9

Задача №3. 13

Список литературы.. 16

Задача №1.

По данным, представленным в таблице, найти параметры уравнения регрессии методом наименьших квадратов. Для проверки адекватности уравнения регрессии определить величину среднего относительного отклонения.

По полученному уравнению регрессии для среднегодовой величины готовой продукции на складе предприятия найти выручку от реализации продукции на следующий год.

Составить бюджет движения денежных средств, определить «критический период» в деятельности предприятия и сделать выводы. Исходные данные для составления бюджета. Объёмы продаж увеличиваются с темпом прироста в месяц 1,5% от базового месяца (декабрь текущего года). Предприятие проводит индивидуальную сбытовую политику на основе применения различных видов реализации при разных условиях оплаты: 25% изделий реализуется за наличный расчет; 75%- с отсрочкой платежа на условиях 3/10 брутто 30: 80% оплачивается в следующем месяце из них 25% со скидкой, а 20%  оплачивается с задержкой ещё на один месяц.

Сырьё закупается в размере потребности следующего месяца, оплата поставщикам производится через месяц. Прогнозируемое увеличение цен на сырьё 3% в месяц.

Издержки определяются в % от выручки базового месяца, из них условно-переменные: сырье-40; условно-постоянные: заработная плата-15; аренда производственных площадей- 10; прочие расходы-5. Уровень инфляции в месяц 2%. Аренда и заработная плата выплачивается в месяц, следующий за месяцем их возникновения. Единый социальный налог составляет 35,6% от заработной платы. Ставка налога на прибыль 24%.

В конце каждого квартала (март, июнь, сентябрь, декабрь) планируется вкладывать в модернизацию производства (определяется студентом самостоятельно) р. Остаток денежных средств на 1 января составляет   (определяется студентом самостоятельно) р. Этой суммы недостаточно и решено иметь целевой остаток (определяется студентом самостоятельно) р. Его величина в последующие месяцы изменяется пропорционально темпу инфляции.

Млн. руб.

X	15,6	10,0	11,5	34,4	27,0	24,2	11,9	18,4	22,6	22,3	15,2	17,8	27,9	19,8	18,1
Y	4,6	2,9	3,8	9,8	12,7	7,7	3,5	5,2	7,4	7,1	4,8	4,9	8,2	6,6	5,5
X	23,3	23,0	30,5	17,0	18,6	24,6	25,7	32,3	31,1	37,9	33,2	18,5	18,4	12,3	23,7
Y	7,3	7,1	9,9	5,7	7,3	5,2	7,8	11,7	11,8	11,1	12,3	6,7	6,1	4,4	10,1

Решение:

На основании данных о динамике показателя (выручка от реализации продукции) можно построить приемлемый прогноз. Подобный расчет выполняется на основе авторегрессионных зависимостей. Для этого необходимо провести корреляционно-регрессионный анализ, используя линейную зависимость. Так как в исходных данных имеется один факторный признак- готовая продукция на складе предприятия (Х) и один результативный признак- выручка от реализации, то можно говорить о парной  корреляции.

В данном случае можно полагать, что между указанными признаками не существует строгой функциональной зависимости, а присутствует корреляционная (статистическая) связь.

Предполагается наличие линейной связи между факторным и результативным признаком, т.е. регрессионная модель описывается функцией вида:

Ỳi= a0 +a1*X,

где Ỳi – значение результативного признака; X- значение факторного признака; a0 и a1- параметры уравнения регрессии, которые рассчитываются из системы нормальных уравнений.

Система нормальных уравнений имеет вид:

{                 N*a0+a1*∑X=∑Y

{a0*∑X+ a1*∑(X*X)= ∑X*Y

Для нахождения параметров уравнения регрессии по методу наименьших квадратов составляем расчётную таблицу:

N	X	Y	X*X	X*Y	Ỳi
1	15,6	4,6	243,36	71,76	5,1
2	10,0	2,9	100,00	29,00	3,2
3	11,5	3,8	132,25	43,70	3,7
4	34,4	9,8	1183,36	337,12	11,5
5	27,0	12,7	729,00	342,90	8,9
6	24,2	7,7	585,64	186,34	7,9
7	11,9	3,5	141,61	41,65	3,8
8	18,4	5,2	338,56	95,68	6,0
9	22,6	7,4	510,76	167,24	7,4
10	22,3	7,1	497,29	158,33	7,3
11	15,2	4,8	231,04	72,96	4,9
12	17,8	4,9	316,84	87,22	5,8
13	27,9	8,2	778,41	228,78	9,2
14	19,8	6,6	392,04	130,68	6,5
15	18,1	5,5	327,61	99,55	5,9
16	23,3	7,3	542,89	170,09	7,7
17	23,0	7,1	529,00	163,3	7,6
18	30,5	9,9	930,25	301,95	10,1
19	17,0	5,7	289,00	96,90	5,5
20	18,6	7,3	345,96	135,78	6,0
21	24,6	5,2	605,16	127,92	8,1
22	25,7	7,8	660,49	200,46	8,5
23	32,3	11,7	1043,29	377,91	10,7
24	31,1	11,8	967,21	366,98	10,3
25	37,9	11,1	1436,41	420,69	12,6
26	33,2	12,3	1102,24	408,36	11,0
27	18,5	6,7	342,25	123,95	6,0
28	18,4	6,1	338,56	112,24	6,0
29	12,3	4,4	151,29	54,12	3,9
30	23,7	10,1	561,69	239,37	7,8
Итого	666,8	219,2	16353,46	5392,93

Из таблицы определяем значения n; ∑X; ∑Y; ∑X*X; ∑X*Y; подставляем в систему уравнений и находим параметры уравнений регрессии методом наименьших квадратов:

{30*a0+a1*666,8=219,2

{ a0*666,8+a1*16353,46=5392,93

Из первого уравнения системы выражаем a0, подставляем во второе уравнение и получаем соответственно значение a1:

Ỳi =0,34*X-0,25.

Далее для проверки адекватности уравнения регрессии определяем величину среднего относительного линейного отклонения:

       

E=((1/n)*∑׀ Yi- Ỳi׀   / Yi)*100%

Где Ỳi- расчётное значение результативного показателя по найденным параметрам уравнения регрессии. Если E<15%,то связь между факторным и результативным признаком достаточно тесная, т.е. готовая продукция на складе предприятия непосредственно определяет выручку от реализации.

Используя средства Microsoft Excel, составляем аналогичную таблицу и считаем E. Получаем, что под знаком суммы стоит число 3,3. Следовательно, E равно 11%. Полученное уравнение регрессии пригодно для прогнозных целей, т.к. E=11%<15%.

Следовательно, например, для среднегодовой величины готовой продукции на складе предприятия 15 млн. рублей предполагаемая выручка от реализации  на следующий год составит 0,34*15-0,25=4,85 млн. рублей.

С учетом прогнозного значения выручки от реализации бюджет движения денежных средств составляем в следующей последовательности: денежный приток по подпериодам (месяц); денежный отток по подпериодам (месяц); расчёт сальдо денежного потока по подпериодам (месяц); определение излишка или дефицита денежных средств. Годовая выручка, полученная с помощью регрессионной зависимости, разбивается на двенадцать месяцев.

По условию задачи, субъект хозяйствования прогнозирует на этот период наращивать объёмы продаж с темпом прироста 1,5 % в месяц.

В рамках бюджета планируется дифференциация отпускных цен на продукцию при различных условиях оплаты: 25% изделий реализуется за наличный расчет; 75% с отсрочкой платеже на условиях 3/10 брутто 30, в том числе 80% оплачивается в следующем месяце, из них 25% со скидкой; а 20% оплачивается с задержкой ещё на один месяц.

Условия 3/10 брутто 30 означают, что предоставляется товарный кредит со скидкой 3 %, если оплата производится в течение 10 дней. Максимальный срок расчёта 30 дней, но уже по полной стоимости.

Сырьё закупается в размере потребности следующего месяца, оплата поставщикам производится через месяц. Издержки определяются в процентах от выручки из них условно-переменные: сырьё-40%; условно-постоянные: заработная плата-15%, аренда производственных площадей-10%; прочие расходы-5%. Прогнозируемое увеличение цен на сырьё 3% в месяц. Уровень инфляции в месяц 2%.

Аренда и заработная плата выплачиваются в месяц, следующий за месяцем их возникновением. ЕСН составляет 35,6% от заработной платы. Ставка налога на прибыль 24%.

В конце каждого квартала планируется вкладывать в модернизацию производства 100000 рублей.

Остаток денежных средств на 1 января составляет 129000 рублей (смотри расчёты в электронной таблице Excel). Этой суммы не достаточно и было решено иметь целевой остаток в 25000 рублей. Под целевым остатком понимается желаемый минимум денежных средств на счёте, который целесообразно иметь в качестве страхового запаса, а также для непрогнозируемых расходов. Его величина в последующие месяцы изменяется пропорционально темпу инфляции.

Такой вариант бюджета движения денежных средств предприятия показал, что сальдо денежного потока положительно. В целом на счёте наблюдается излишек денежных средств с учетом целевого сальдо и при финансировании этой стратегии предприятие обходится собственными средствами.

Вывод: Определённые условности являются неизбежным спутником любого расчёта прогнозного характера. Следует помнить, что в такого рода задачах важна не точность расчётов, а выявление некоторых тенденций. Использование бюджетирования в управлении финансами позволяет: заранее оценивать экономическую состоятельность, обеспечивая финансовую устойчивость субъекта хозяйствования; сделать хозяйственную деятельность прозрачной, то есть более привлекательной для наших инвесторов.

Задача №2.

Составить отчёт о прибылях и убытках для фирм «А», «С», «К» и на основании сопоставления коэффициентов PMOS, BEP, ROA, ROE, ROI оценить адекватность проводимых ими финансовых политик различным состояниям экономики. Налог на прибыль 24%. Сценарные условия функционирования фирм и другие показатели заданы в таблице.

Показатель	«А»	«С»	«К»
Выручка при подъёме экономики	1392	1450	1508
Выручка при стабильной экономике	1044	1160	1334
Выручка при спаде экономики	812	928	1218
Акционерный капитал	174	232	290
Краткосрочные кредиты (17,5%)	232	116	58
Долгосрочные кредиты (23,5%)	-	116	232
Затраты на реализацию	232+0,7В	313+0,65В	447+0,6В

Решение:

Три фирмы придерживаются различных финансовых политик: «Агрессор» финансирует свою деятельность за счёт кратко срочных обязательств и собственных источников; «Середняк» придерживается умеренной стратегии согласования сроков своих активов и обязательств; «Консерватор» в основном использует долгосрочные заёмные источники финансирования.

По данным задачи составляем отчёт о прибылях и убытках для каждой фирмы при различных состояниях экономики:

«Агрессор»
Показатель	Состояние экономики
Подъём	Стабильное	Спад
Выручка от реализации	1392	1044	812
Затраты на реализованную продукцию	1207,4	963,8	801,4
Прибыль до вычета процентов и налогов	184,6	80,2	10,6
Проценты к уплате	40,6	40,6	40,6
Прибыль до вычета налогов	144	39,6	-30
Налог на прибыль(24%)	34,56	9,5	-
Чистая прибыль	109,44	30,1	-
«Середняк»
Показатель	Состояние экономики
Подъём	Стабильное	Спад
Выручка от реализации	1450	1160	1334
Затраты на реализованную продукцию	1255,5	1067	1180,1
Прибыль до вычета процентов и налогов	194,5	93	153,9
Проценты к уплате	47,56	47,56	47,56
Прибыль до вычета налогов	146,94	45,44	106,34
Налог на прибыль(24%)	35,27	10,9	25,52
Чистая прибыль	111,67	34,54	80,82
«Консерватор»
Показатель	Состояние экономики
Подъём	Стабильное	Спад
Выручка от реализации	1508	1334	1218
Затраты на реализованную продукцию	1351,8	1247,4	1177,8
Прибыль до вычета процентов и налогов	156,2	86,6	40,2
Проценты к уплате	64,67	64,67	64,67
Прибыль до вычета налогов	91,53	21,93	-24,47
Налог на прибыль(24%)	21,97	5,26	-
Чистая прибыль	69,56	16,67	-

Определение финансовых показателей является обычно первым шагом финансового аналитика. Весомость обязательств фирмы и способность выплатить их можно установить сравнением долгов с активам предприятия. Такие сравнения делаются на основе анализа коэффициентов. На основании сопоставления коэффициентов рентабельности определяем положение, какой из фирм лучше при различных состояниях экономики. На западе пользуются следующими показателями рентабельности:

Коэффициент рентабельности реализованной продукции (PMOS)- отношение чистой прибыли к выручке от реализации.

Коэффициент генерирования доходов (BEP)- отношение прибыли до вычета процентов и налогов к сумме активов.

Коэффициент рентабельности активов (ROA)- отношение чистой прибыли к сумме активов.

Коэффициент рентабельности собственного капитала (ROE)- отношение чистой прибыли к собственному капиталу.

Коэффициент рентабельности инвестированного капитала (ROI)- отношение чистой прибыли и процентов к уплате к общему капиталу.

Рассчитанные коэффициенты рентабельности (%) приведены в таблице:

«Агрессор»
Показатель	Состояние экономики
Подъём	Стабильное	Спад
PMOS	7,8	2,9	-
BEP	45,5	19,8	2,6
ROA	27	7,4	-
ROE	62,9	17,3	-
ROI	37	17,4	-
«Середняк»
Показатель	Состояние экономики
Подъём	Стабильное	Спад
PMOS	7,7	3	6
BEP	41,9	20	33,2
ROA	24,1	7,4	17,4
ROE	48,1	14,9	34,8
ROI	34,3	17,7	27,7
«Консерватор»
Показатель	Состояние экономики
Подъём	Стабильное	Спад
PMOS	4,6	1,2	-
BEP	26,9	14,9	6,9
ROA	12	2,9	-
ROE	24	5,7	-
ROI	23,1	14	-

Вывод: При заданных сценарных условиях коэффициенты рентабельности показывают: если экономика находится в состоянии подъёма, то наиболее эффективная политика у фирмы «Агрессор»; если экономика стабильна, то самые высокие финансовые коэффициенты уже у фирмы «Середняк»; если в экономике наблюдается спад, то единственной фирмой, не несущей убытки является фирма «Середняк».

Задача №3.

Требуется построить дерево решений для оценки риска и определить привлекательность инвестиционного проекта, рассчитанного на два года. Проект требует первоначальных вложений 185000 USD и финансируется за счёт банковской ссуды. Ожидается, что процентная ставка будет меняться по годам следующим образом: 14%, 16%. Распределение вероятностей денежного потока представлено в таблице:

CF1=78500	P1=0,28	CF1=132000	P1=0,36	CF1=144000	P1=0,36
CF2i	P2i	CF2i	P2i	CF2i	P2i
93700	0,17	81500	0,22	95600	0,32
105800	0,51	117400	0,35	124900	0,29
112300	0,32	149100	0,43	141600	0,39

Решение:

Деревья решений обычно применяются для анализа риска проектов, имеющих разумное число вариантов развития. Они особо полезны в ситуациях, когда финансовые решения зависят от решений принятых ранее, и в свою очередь определяют сценарий дальнейшего развития событий.

Дерево решений имеет вид нагруженного графа и его вершины – это ключевые состояния, в которых возникает необходимость выбора, а дуги – различные события, имеющие место в ситуации, определяемой вершиной. В общем случае использование данного метода предполагает наличие следующих шагов:

1.Для каждого момента времени определяют проблему и все возможные варианты событий.

2. Откладывают на дереве соответствующую проблеме вершину и исходящие из него дуги.

3. Каждой исходящей дуге приписывают её денежную и вероятностную оценку.

4. Исходя из значений всех вершин и дуг, определяют вероятное значение рассматриваемого критерия.

5. Проводят анализ вероятностных распределений полученных результатов.

Дерево решений для этого проекта представлено на рисунке ниже.

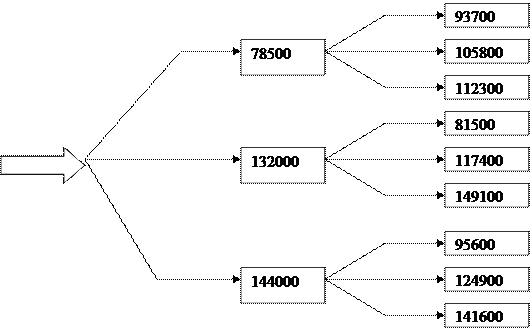                                                                     0,17

                                                                    0,51

                        О,28                                    0,32

                                                                     0,22

                        0,36                                      0,35

                                                           0,43

                                                           0,32

          0,36                                          0,29

Определяем суммарный денежный поток проекта:

Путь	CF1	CF2i	PVi	P1,2i	PVi *P1,2i
1	78500	93700	-46506	0,0476	-2213,69
2	78500	105800	-37513,7	0,1428	-5356,96
3	78500	112300	-32683,2	0,0896	-2928,41
4	132000	81500	-8642,75	0,0792	-684,51
5	132000	117400	18036,8	0,126	2272,64
6	132000	149100	41595,06	0,1548	6438,92
7	144000	95600	12362,16	0,1152	1424,12
8	144000	124900	34136,84	0,1044	3563,89
9	144000	141600	46547,66	0,1404	6535,29
M(PV)	9051,29

Значения PVi  рассчитаны по формуле

PVi  = - 185000 + (CF1/(1+0,14))+( CF2i/(1+0,16)*(1+0,16))

Значения P1,2i здесь представляют собой совместные вероятности двух событий P1,2i=P1*P2.

Суммарная ожидаемая PV определена как сумма произведений P1,2i и PVi.

Вывод: поскольку суммарная ожидаемая PV положительна (9051,29 USD), при отсутствии других альтернатив проект можно принять. В общем случае предпочтение следует отдавать проектом с большей суммарной PV.

Список литературы

1.     Савицкая Г.В. Анализ хозяйственной деятельности предприятия: 4-е изд., перераб. и доп. – Минск: ООО «Новое знание», 2000. – 320 с.

2.     Управление инвестициями: В 2 т.Т.2 / Под ред. В.В. Шеремета.- М.: Высш.шк.,2002.-560 с.

3.     Финансовый менеджмент: теория и практика/ Под ред. Стояновой Е.С.- М.: Перспектива, 2003. – 267 с.

4.     Финансовый менеджмент: Учебно-практическое руководство./Под редакцией Е.С. Стояновой. – М.: Перспектива, 2000. – 780 с.

5.     Шеремет А.Д Методика финансового анализа / А.Д. Шеремет, Р.С. Сайфулин.- М.: Инфра- М,2001.-256 с.