Имеются выборочные данные о глубине вспашки полей под озимые культуры Х (см) и их урожайности Y (ц с га) (табл. 1).

Таблица 1

Исходные данные

1. Составить уравнение линейной регрессии y = a + bx +ε, используя МНК, и найти числовые характеристики переменных.

2. Составить уравнение линейной регрессии y = a + bx +ε, используя матричный метод.

3. Вычислить коэффициент корреляции и оценить полученное уравнение регрессии.

4. Найти оценки параметров а, b, δ².

5. Найти оценки параметров нормального распределения для статистик а¯ и b¯.

6. Найти доверительные интервалы для а и b на основании оценок а¯ и b¯ при уровне значимости а = 0,05.

7. Вычислить коэффициент детерминации и оценить качество выбранного уравнения регрессии.

Решение:

Используя исходные данные, строим диаграмму рассеяния (рис. 1):

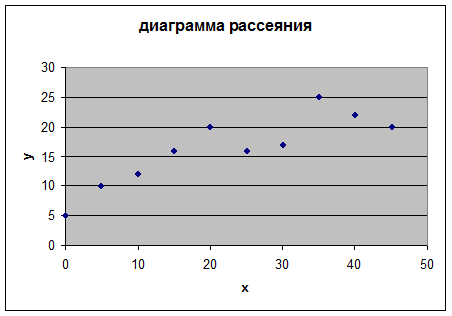
Рисунок 1 – Диаграмма рассеяния

Полагаем, что связь между факторами Х и У может быть описана линейной функцией.

Нормальные уравнения для линейного тренда имеют вид:

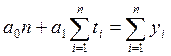
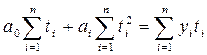
где: y_i - уровни исходного ряда динамики;

        t_i - номера периодов или моментов времени (1,2,3:n);

        n - число уровней ряда;

        а₀, а₁, а₂ - константы уравнений.

Решение задачи нахождения оценок а и b основывается на применении метода наименьших квадратов (сокращенно - МНК), суть которой в следующем: нахождение оценок а и b неизвестных параметров α и β сводится к следующей экстремальной задаче функции двух переменных  F(a,b):

 ,

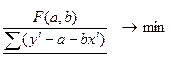которая в свою очередь сводится к системе двух линейных уравнений с двумя неизвестными а и b:

Решение этой системы можно получить по правилу Крамера:

;

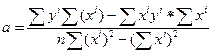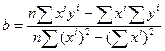
Обозначим через  ;  выборочные средние наблюдаемых значений переменных х и у. Таким образом, оценки а и b можно искать по следующим формулам:

;  .

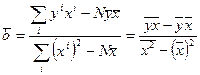Для этого организуем вычисления во вспомогательной табл. 2.

                                                                          Таблица 2

Вспомогательная таблица для определения параметров уравнения линейной регрессии

Тогда

.

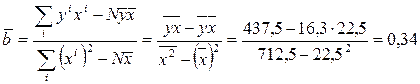
Значит, уравнение линейной регрессии имеет вид:

.

Вычислим коэффициент корреляции по формуле:

.

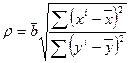Для применения формулы составим вспомогательную табл. 3:

Таблица 3

Вспомогательная таблица для расчета коэффициента корреляции

Тогда коэффициент корреляции найдется следующим образом:

.

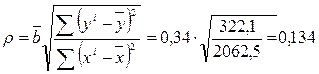Определим значимость регрессии для  a = 0,05, проверив гипотезу Н₀: «b=0», рассчитав статистику:

.

По таблице F-статистики найдем критическое значение этого критерия:

5,32

Т.к. F>f_кр, то гипотезу Н₀: «b=0» отвергаем, т.е. регрессия значима.

Найдем 95%-ные доверительные интервалы для параметров модели. Для этого вначале найдем параметры распределения Стьюдента, оформив вспомогательную табл. 4:

Таблица 4

Таблица для расчета доверительных интервалов для параметров модели

Оценка дисперсии случайной составляющей эконометрической модели вычисляется по формуле .

Используя результаты регрессионной статистики, получаем:

.

Величина доверительного интервала определяется в общем виде следующим образом:

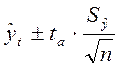
где  - среднее квадратическое отклонение от тренда;

t_a - табличное значение t-критерия Стьюдента при уровне значимости a. Зависит от уровня значимости a (%) и числа степеней свободы k=n-m.

Величина  определяется по формуле

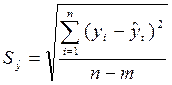
где: y_i и - соответственно фактические и расчетные значения уровней динамического ряда;

n - число уровней ряда;

m - количество параметров в уравнении тренда (для уравнения прямой m=2).

Параметры нормального распределения Стьюдента:

.

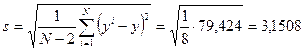Тогда, по таблице значений критерия Стьюдента, .

Тогда искомые доверительные интервалы:

Для коэффициента а:  .

Для коэффициента b:  .

Коэффициент детерминации рассчитывается по формуле

.

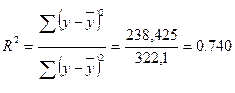Очевидно, что 0£ R² £ 1. Значение R²  характеризует ту долю дисперсии переменной у, которая обуславливается уравнением регрессии ŷi = a +bx. Таким образом,  чем ближе значение R² к единице, тем точнее уравнение регрессии отражает имеющуюся зависимость между переменными.

Так как R² достаточно близок  к единице, то уравнение регрессии достаточно точно отражает истинную зависимость между данными о глубине вспашке полей и их урожайности.

Задача 2

1. Составить уравнение множественной линейной регрессии y = a + b₁x₁ + b₂x₂ + ε в матричной форме, используя МНК, и найти числовые характеристики переменных.

2. Найти оценки параметров а, b₁, b₂, δ²

3. Найти коэффициент детерминации и оценить уравнение регрессивной связи.

4. Оценить статистическую значимость между переменными.

Изучается зависимость по предприятиям объединения потребления материалов Y(т) от энерговооруженности труда Х₁ (кВт/ч на одного рабочего) и объема производственной продукции Х₂ (тыс. ед.) (табл. 5).

Таблица 5

Исходные данные

Решение:

Для подстановки числовых коэффициентов в систему уравнений, используемую в методе наименьших квадратов, составим вспомогательную табл. 6:

Таблица 6

Вспомогательная таблица для вычисления числовых коэффициентов уравнения регрессии

Тогда система уравнений имеет вид:

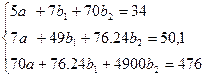
Найдем оценки для параметров модели, решая систему уравнений методом Крамера:

 =

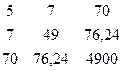Δ = 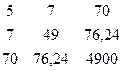  = 5  - 7  + 70  = 5 (76.24*76.24 - 49*4900 ) - 7 (70*76.24 - 7*4900 ) + 70 (70*49 - 7*76.24 ) = - 5 *234287.46 + 7 * 28963,2 + 70*2896,32 = - 1171437,3 + 202742,4 + 202742,4 =  -765952,5

а =  Δа / Δ

Δа = 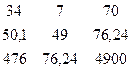   = 34  - 7  + 70 = 34 (76,24*76,24 - 49*4900 ) - 7 (476*76,24 - 50,1*4900) + 70 (476*49 - 50,1*76,24 ) = - 34 * 234287,46 + 7 * 209199,76 + 70* 19504,376 = -7965773,64 + 1464398,32 + 1365306,32 = -5136069

а =  Δа / а = -5136069 / -765952,5= 6,705

b₁ = Δ b₁ / Δ

Δ b₁ = 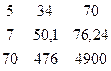   = 5  - 34  + 70  = 5 (476*76,24 - 50,1*4900 ) - 34 (70*76,24 - 7*4900 ) + 70 (70*50,1 - 7*476) = - 5 * 209199,76 + 34 * 28963,2 + 70 * 175 = -1045998,8 + 984778,8 + 12250 = -48970

b₁ = Δ b₁ / Δ = - 48970 / -765952,5= 0,0639

b₂ = Δ b₂ / Δ

Δ b₂ = 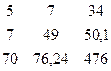  = 5  - 7  + 34 = 5 (76,24*50, - 49*476 ) - 7 (70*50,1 - 7*476 ) + 34 (70*49 - 7*76,24 ) = - 5 * 19504,376 -  7 *175 + 34 * 2896,32 = - 97521,88 - 1225 + 98474,88 = -271,92

b₂ = Δ b₂ / Δ = -271,92 / -765952,5= 0,00035

Тогда уравнение регрессии имеет вид:

Оценка дисперсии случайной составляющей эконометрической модели вычисляется по формуле .

Используя результаты регрессионной статистики, получаем:

.

Для применения формулы для нахождения коэффициента детерминации составим вспомогательную табл. 7:

Таблица 7

Вспомогательная таблица для нахождения коэффициента детерминации

Отсюда коэффициент детерминации:

.

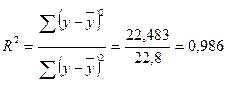Чем ближе коэффициент детерминации к единице, тем лучше построена модель зависимости результирующего показателя у от фактор – признака х.

Так как R² достаточно близок  к единице, то уравнение регрессии достаточно точно отражает истинную зависимость.

Величина r_xy – коэффициент парной корреляции сложных величин х и у.

Содержательный смысл этого коэффициента таков: он показывает на сколько стандартных единиц изменится показатель у, если фактор – признак х увеличится на 1 свою стандартную единицу.

Коэффициент корреляции является показателем тесноты линейной зависимости.

-1 < r_xy < 1

r_xy > 0, то прямая положительная корреляционная зависимость.

r_xy < 0 – то обратная.

Так как в задаче парная линейная зависимость, то воспользуемся при решении формулой коэффициента корреляции:

 где r – парный коэффициент корреляции,

 - среднее произведение факторного и результативного признаков,

 -произведение средних размеров факторного и результативного признаков,

,  - среднее квадратическое отклонение факторного и результативного признаков. Причем

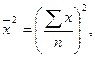
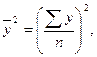
Оценим статистическую зависимость между потреблением материалов от энерговооруженности труда (Y от x₁)

 = 50,1/5 = 10,02

 = 7/5 = 1,4

 = 34/5 = 6,8

 = 1,4*6,8 = 9,52

 = 10,14/5 = 2,028

 = 254/5 = 50,8

 = 1,4² = 1,96

 = 6,8² = 46,24

r_xy > 0, то прямая положительная корреляционная зависимость.

Оценим статистическую зависимость между потреблением материалов от объема производственной продукции (Y от x₂)

 = 476/5 = 95,2

 = 70/5 = 14

 = 34/5 = 6,8

 = 14*6,8 = 95,2

 = 1030/5 = 206

 = 254/5 = 50,8

 = 14² = 196

 = 6,8² = 46,24

r_xy = 0, следовательно, между х и у отсутствует корреляционная зависимость. В этом случае отсутствует линейная зависимость.

Список литературы

1.                Вентцель Е.С. Теория вероятностей. М.: 1972г.

2.     Боярский А.Я., Громыко Г.Л. Общая теория статистики М.: изд. Московского университета, 1985 г. – 372 с.

3.                Гмурман В.Е.  Теория вероятностей и математическая статистика:- М.: 2002.

4.     Елисеева И.И. Статистика – М.: ТК Велби, Изд-во Проспект, 2004. – 448 с.

5.     Ефимова М.Р. Общая теория статистики Изд. 2 – е, испр. И жоп. – М.: ИНФРА – М, 2002. – 416 с.