Содержание:

Задача №1. 3

Задача №2. 4

Задача №3. 5

Задача №4. 6

Задача №5. 7

Задача №6. 8

Задача №1

Пассив коммерческого банка содержит следующие статьи: вклады до востребования – В, срочные вклады – Т, собственный капитал – К. Норматив минимального резервного покрытия про вкладам до востребования равен НВ, по срочным НТ. На какую сумму банк может увеличить сумму выдаваемых кредитов, если все вклады до востребования будут переоформлены в срочные? Чему будет равна общая сумма выданных кредитов?

В (млн. руб.)                                 460,2

Т (млн. руб.)                                 255,5

К (млн. руб.)                                 109,7

НВ (%)                                           14,9

НТ (%)                                           11,0

Решение:

Объем кредитов которые банк может выдать, используя средства вкладов до востребования найдем по формуле:

1) Найдем возможный объем кредитов, который банк может выдать

КВ=(1-НВ)В= 1 - 0,149=391,6302, так как 14,9% банк обязан перечислить в резервы центрального банка

Объем кредитов которые банк может выдать, используя средства срочных вкладов

КТ=(1-НТ)×Т= 227, 395, так как 11% банк обязан перечислить в резервы центрального банка

Итого сумма кредитов, которую банк может выдать составляет

КТ+КВ= 619,0252

2) Найдем возможный объем кредитов, который банк может выдать после переоформления всех кредитов в срочные

Если все вклады до востребования будут переоформлены в срочные, тогда объем вкладов составит

,

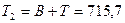
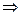
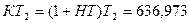т.о., банк может увеличить сумму выдаваемых кредитов, если все вклады до востребования будут переоформлены в срочные на

КТ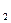 – КТ – КВ = 636,973 - 619,0252 =17,9478 млн. рублей, а общая сумма кредитов составит 636,973 млн.рублей.

Задача №2

Реальный ВВП увеличился в N раз. Денежная масса выросла на М процентов. Скорость обращения денег – стабильна. Как изменился уровень цен?

N                                                    1,4

М(%)                                              7,6

Решение:

Находим по формуле «уравнение обмена» MV=PQ, где

Q – физическое количество товаров и услуг

P – средневзвешенная цена всех проданных товаров и услуг

V – скорость обращения денег

М – суммарный денежный запас

Введем следующие обозначения:

Q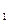- физическое количество товаров и усулг до изменения цен,

Q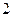- физическое количество товаров и усулг после изменения цен, тогда

,

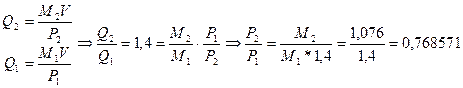т.о. уровень цен снизится примерно на 23,2%

Задача №3

Как изменится реальный доход, если номинальное предложение денег увеличится на М%, уровень цен возрастет на Р%, а скорость обращения денег неизменна.

М(%)                                            6,1

Р(%)                                             7,6

Решение:

MV=PQ

V=const

Введем следующие обозначения:

M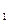- суммарный денежный запас до изменений,

M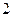- суммарный денежный запас после изменений

Р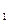- средневзвешенная цена всех проданных товаров и услуг до изменений,

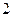Р- средневзвешенная цена всех проданных товаров и услуг после изменений, т.о.

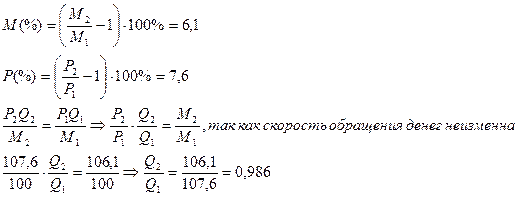
Таким образом, реальный доход изменится на 1,14%

Задача №4

Спрос на наличность составляет Н% от суммы  депозитов. Норма резервирования равна Р%. ЦБ решил расширить предложение денег на М. Чему равно увеличение денежной базы?

Н (%)                                          9,3

Р(%)                                         14,8

М(млрд.руб.)                           382,0

Решение:

Денежная база равна сумме наличности (CU) и резервов коммерческих банков

H=CU+R

Предложение денег определяется по формуле:

SM=CU+D, где

D – депозиты

Соотношение между предложением денег и денежной базой представим следующим образом (формула денежного мультипликатора):

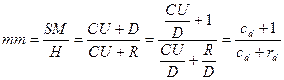,где

,

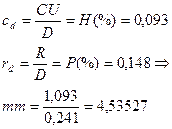
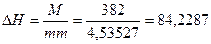т.о. увеличение денежной базы при расширении предложении денег на 382 млрд. рублей составит 84,2287 млрд. рублей.

Задача №5

Облигация номиналом Н, ставкой купонного дохода – К, и сроком погашения 6 лет продается на рынке. Определить стоимость облигации, если доходность  рынка равна Д.

Н, руб.                                     9285,3

К,%                                          4,9

Д,%                                          8,1

Решение:

Определение текущей стоимости потока платежей находим по формуле

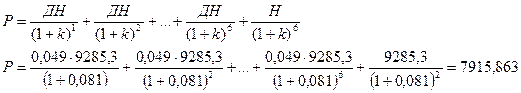
Где ДН = К(%)H – ежегодные выплаты по облигации

Таким образом, стоимость облигации равна 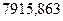 рублей

Задача №6

Предприятие приобрело здание по цене Р на следующих условиях: а) X% от стоимости оплачивается немедленно, б) оставшаяся часть погашается равными годовыми платежами в течение 10 лет с начислением М% годовых на непогашенную часть кредита по схеме сложных процентов. Определить велечину годового платежа.

Р, руб.                                    11 342 620,7

X,%                                         27,2

М,%                                         11,5            

Решение:

Пусть

k – величина годового платежа

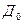- сумма долга (кредита) за здание

Приведем стоимость денежных потоков к базису последнего года:

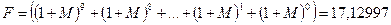 - дисконтирующий коэффициет суммы выплат по кредиту, тогда

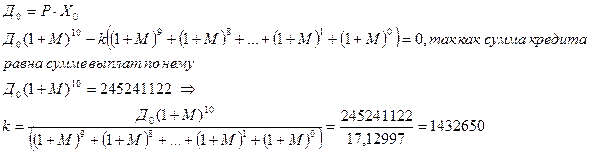
Таким образом, величина годового платежа составляет 1432650 рублей.