При изучении теории вероятностей приходится использоватъ понятия случайного события и случайной величины. При этом предсказать заранее результат испытания, в котором может появиться или не появиться то или иное событие или какое-либо определенное значение случайной величины, невозможно, так как исход испытания зависит от многих случайных причин, не поддающихся учету.

Однако при неоднократном повторении испытаний могут наблюдаться определенные закономерности. Эти закономерности, свойственные массовым случайным явлениям, и изучает теория вероятностей. Следует отметить, что математические законы теории вероятностей получены в результате абстрагирования реальных ситуаций, в которых наблюдаются случайные массовые явления.[1]

При изучении результатов наблюдений над реальными случайными массовыми явлениями также имеют место некоторые закономерности. Следует обратить внимание на то, что они обладают свойством устойчивости. Суть этого свойства состоит в том, что конкретные особенности каждого отдельного случайного явления почти не сказываются на среднем результате большой массы подобных явлений, а характеристики случайных событий и случайных величин, наблюдаемых в испытаниях, при неограниченном увеличении числа испытаний становятся практически не случайными.

Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в теоремах, носящих общее название закона больших чисел.[2] Под законом больших чисел не следует понимать какой-то один общий закон, связанный с большими числами. Закон больших чисел - это обобщенное название нескольких теорем, из которых следует, что при неограниченном увеличении числа испытаний средние величины стремятся к некоторым постоянным.                                           

Глава 1. История открытия закона больших чисел

Первая точно доказанная теорема принадлежит Я.Бернулли (опубликована после его смерти, в 1713). Теорема Бернулли была обобщена С. Пуассоном, в сочинении которого "Исследование о вероятности суждения" (1837) впервые появился термин " закон больших чисел ". Значительно более общее понимание этого термина основано на работе П. Л. Чебышева "О средних величинах" (1867).  В этом современном понимании Б. ч. з. утверждает, что при некоторых подлежащих точному указанию условиях среднее арифметическое 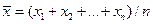  достаточно большого числа n независимых случайных величин X_k с вероятностью, сколь угодно близкой к единице, сколь угодно мало отличается от своего математического ожидания.

Условие независимости слагаемых в большинстве применений закона больших чисел если и выполняется, то лишь с тем или иным приближением. Поэтому важно исследование условий применимости закона больших чисел к случаю зависимых слагаемых. Основные математические работы в этом направлении принадлежат А. А. Маркову, С. Н. Бернштейну и А. Я. Хинчину.[3]

Глава 2. Теорема Бернулли

 Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А равна р. Можно ли предвидеть какова будет примерно относительная частота появлений события? Положительный ответ на этот вопрос дает теорема, доказанная Яковом Бернулли, которая получила название «закона больших чисел» и положила начало теории вероятностей как науке. Доказательство Бернулли было сложным; простое доказательство дано П. Л. Чебышевым в 1846 г.

Теорема Бернулли. Если в каждом из п независимых испытаний вероятность р появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.

Другими словами, если 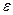 сколь угодно малое положительное число, то при соблюдении условий теоремы будет иметь место равенство

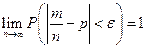
Глава 3. Закон больших чисел в форме Чебышева.

Теорема Чебышева. Если X₁, Х₂, ...Х_п попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то как, бы мало ни было положительное число 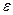, вероятность неравенства  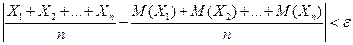будет как угодно близка к единице, если число случайных величин достаточно велико.

Итак, среднее арифметическое  достаточно большого числа  независимых случайных величин (дисперсии которых равномерно ограничены) утрачивает характер случайной   величины. Объясняется это тем, что отклонения каждой из величин от своих математических ожиданий могут быть как положительными, так и отрицательными, а в среднем арифметическом они взаимно погашаются.

Теорема Чебышева справедлива не только для дискретных, но и для непрерывных случайных величин; она является ярким примером, подтверждающим справедливость учения диалектического материализма о связи между случайностью и необходимостью.[4]

Глава 4. Значение закона больших чисел для практики

Обычно для измерения некоторой физической величины производят несколько измерений и их среднее арифметическое принимают в качестве искомого размера. При каких условиях этот способ измерения можно считать правильным? Ответ на этот вопрос дает теорема Чебышева. Действительно, рассмотрим результаты каждого измерения как случайные величины Х₁, Х₂, ..., Х_п. К этим величинам можно применить теорему Чебышева, если: 1) они попарно независимы, 2) имеют одно и то же математическое ожидание, 3) дисперсии их равномерно ограничены.

Первое требование выполняется, если результат каждого измерения не зависит от результатов остальных.

Второе требование выполняется, если измерения произведены без систематических (одного знака) ошибок. В этом случае математические ожидания всех случайных величин одинаковы и равны истинному размеру а.

Третье требование выполняется, если прибор обеспечивает определенную точность измерений. Хотя при этом результаты отдельных измерений различны, но рассеяние их ограниченно.

Если все указанные требования выполнены, мы вправе применить к результатам измерений теорему Чебышева: при достаточно большом п вероятность неравенства 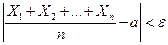как угодно близка к единице. Другими словами, при достаточно большом числе измерений почти достоверно, что их среднее арифметическое как угодно мало отличается от истинного значения измеряемой величины.

Итак, теорема Чебышева указывает условия, при которых описанный способ измерения может быть применен.

Однако ошибочно думать, что увеличивая число измерений можно достичь сколь угодно большой точности. Дело в том, что сам прибор дает показания лишь с точностью ±а; поэтому каждый из результатов измерений, а следовательно и их среднее арифметическое, будут получены лишь с точностью, не превышающей точности прибора.

На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности (генеральной совокупности) исследуемых объектов. Например, о качестве кипы хлопка заключают по небольшому пучку, состоящему из волокон, наудачу отобранных из разных мест кипы. Хотя число волокон в пучке значительно меньше, чем в кипе, сам пучок содержит достаточно большое количество волокон, исчисляемое сотнями.

В качестве другого примера можно указать на определение качества зерна по небольшой его пробе. И в этом случае число наудачу отобранных зерен мало сравнительно со всей массой зерна, но само по себе оно достаточно велико.

Из приведенных примеров можно заключить, что для практики теорема Чебышева имеет неоценимое значение.

Глава 5. Закон больших чисел и предельные теоремы

Для независимых случайных величин, имеющих одинаковые распределения вероятностей и конечное математическое ожидание а, закон больших чисел утверждает, что при любом 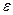 > 0 вероятность неравенства

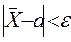
стремится к единице при 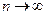. Порядок отклонений  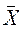от а указывается предельными теоремами теории вероятностей. В типичных случаях отклонения имеют порядок . Соответственно, случайные отклонения суммы 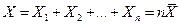 от её математического ожидания na растут как.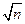

Этот факт, называемый "законом корня квадратного из n" даёт некоторое, хотя и грубое, представление о характере действия закона больших чисел.

Наглядное объяснение смысла и значения закона больших чисел даёт следующий пример. Пусть в замкнутом сосуде заключено N молекул газа. В соответствии с кинетической теорией каждая молекула беспорядочно движется внутри сосуда, испытывая множество столкновений с другими молекулами и стенками сосуда. Ударяясь о какую-либо площадку s стенки в течение выбранного промежутка времени в t секунд, отдельная молекула сообщает этой площадке импульс f_k. Импульс f_k является типичной случайной величиной, т.к. состояние рассматриваемого газа определяет лишь математическое ожидание а = E (f_k) этого импульса, фактическое же значение импульса данной молекулы за данный промежуток времени может быть самым различным (начиная от нуля - в случае, если за данный промежуток времени данная молекула не ударялась о площадку s). Сумма 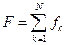 импульсов всех молекул, сообщаемых площадке s за данный промежуток времени, является также случайной величиной с математическим ожиданием, равным А = Na. Однако в силу закона больших чисел (который проявляется здесь с исключительной точностью благодаря тому, что число N очень велико) F в действительности оказывается почти независимым от случайных обстоятельств движения отдельных молекул, а именно - почти точно равным своему математическому ожиданию А. Этим, с точки зрения кинетической теории, и объясняется тот факт, что давление газа на площадку s является практически строго постоянным, а не колеблется беспорядочно.

Часто приходится применять закон больших чисел и в такой обстановке, когда количество случайных слагаемых не столь велико, как в примере с газовыми молекулами; тогда отклонения суммы случайных величин от её математического ожидания могут быть значительными. В этом случае крайне важно уметь оценивать размеры этих отклонений. Пусть, например, из 1000 партий каких-либо изделий, по 100 шт. в каждой, взято для испытания наудачу по 10 шт. из каждой партии и среди испытанных 10 000 шт. обнаружено 125 дефектных. Если обозначить n_к число дефектных изделий в k-й партии, то общее число дефектных изделий равно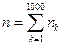математическое ожидание числа дефектных изделий среди тех десяти, которые взяты для испытаний из k-й партии, равно S_k = (¹⁰/₁₀₀) n_k, а математическое ожидание общего числа дефектных изделий в 1000 пробах по 10 штук равно 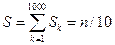. В силу закона больших чисел естественно считать, что 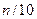~ 125, т. е. среди 100 000 изделий во всех партиях имеется приблизительно 1250 дефектных. Более точное исследование с помощью теории вероятностей приводит к такому результату: если выборка изделий из каждой партии была действительно случайной, то можно с достаточной уверенностью утверждать, что фактически 1000 < n < 1500, но уже оценка 1100 < n < 1400 не была бы достаточно надёжной, а для оценки 1200 < n < 1300 совсем не имеется серьёзных оснований. Получить более точную оценку для n можно, лишь испытав большее число изделий.

Условие независимости слагаемых в большинстве применений закона больших чисел если и выполняется, то лишь с тем или иным приближением. Так, уже в первом примере движения отдельных молекул газа нельзя, строго говоря, считать независимыми. Поэтому важно исследование условий применимости закона больших чисел к случаю зависимых слагаемых. Качественно результаты  исследований сводятся к тому, что закон больших чисел  применим, если между слагаемыми с далёкими номерами зависимость достаточно слаба. Таково, например, положение в рядах метеорологических наблюдений над температурой или давлением воздуха.

Заключение

Как мы знаем, нельзя заранее уверенно предвидеть, какое из возможных значений примет случайная величина в итоге испытания; это зависит от многих случайных причин, учесть которые мы не в состоянии. Казалось бы, что поскольку о каждой случайной величине мы располагаем в этом смысле весьма скромными сведениями, то вряд ли можно установить закономерности поведения и суммы достаточно большого числа случайных величин. На самом деле это не так. Оказывается, что при некоторых сравнительно широких условиях суммарное поведение достаточно большого числа случайных величин почти утрачивает случайный характер и становится закономерным.[5]

Закон больших чисел - одно из основных положений теории вероятностей, в силу которого совокупность действия большого числа случайных факторов приводит, при некоторых весьма общих условиях, к результату, почти не зависящему от случая. Закон больших чисел имеет важное практическое значение в статистике, физике и других отраслях знаний при изучении массовых явлений.

Список литературы

1.                         Гнеденко Б. В., Курс теории вероятностей, 4 изд., М., 1965.

2.                     Гмурман В.Е. Теория вероятностей и математическая статистика. – М: Высшая школа, 1997.

3.                     Калинина В.Н., Панкин В.Ф.    Математическая статистика: Учебник. - М.: Высшая школа, 1998.

4.                     Математическая энциклопедия. Т.1 – М: «Советская Энциклопедия», 1977.

5.                     Семенов А.Д. Теория вероятностей и математическая статистика: учебник для ВУЗов. – М.: Инфра-М., 2003.

[1] Калинина В.Н., Панкин В.Ф.    Математическая статистика: Учебник. - М.: Высш. школа, 1998.

[2] В.Е. Гмурман Теория вероятностей и математическая статистика. – М: Высшая школа, 1997, с.94.

[3] Математическая энциклопедия. Т.1 – М: «Советская Энциклопедия», 1977, с.527

[4] В.Е. Гмурман Теория вероятностей и математическая статистика. – М: Высшая школа, 1997, с.100.

[5] В.Е. Гмурман Теория вероятностей и математическая статистика. – М: Высшая школа, 1997, с.94