Динамические ряды
1. Метод анализа временных рядов
Прогнозы часто
осуществляются на основе некоторых статистических показателей, которые
изменяются во времени. Если эти показатели имеют значения на определенные
промежутки времени, следующие друг за другом, то образуются некоторые ряды
данных с определенными тенденциями. Ряд
расположенных в хронологической последовательности значений статистических
показателей, представляют собой временной (динамический) ряд.
Динамическим рядом
называется ряд чисел или ряд однородных статистических величин, показывающих
изменения размеров какого-либо явления или признака во времени. В
зависимости от составляющих величин различают три основных типа динамических
рядов:
-
динамические ряды, построенные из абсолютных величин
(показатели реализации продукции, затраты на продвижение и т.д.)
-
ряды динамики, представленные относительными
величинами и демонстрирующие изменения каких-либо коэффициентов (изменение
товарооборота, цен, рождаемости и т.д.); такие ряды называются сложными или
производными, потому что коэффициенты вычисляются на основании абсолютных
показателей.
- динамические ряды,
состоящие из средних величин, например, показателей потребления товара на душу населения, среднего дохода, средних цен за период
времени и т.д.
Каждый временной ряд состоит из двух
элементов: отрезки времени (периоды), в рамках которых был зафиксирован
определенный статистический показатель и статистические показатели,
характеризующие объект исследования (уровни ряда).
Если
уровень приведенного динамического ряда характеризует исследуемый параметр за
определенный промежуток времени – день, месяц, квартал, год и т.д., то такие
динамические ряды получили название интервальных. Если уровень
динамического ряда характеризует величину на определенный момент времени, например,
на определенную дату, то такие ряды называются моментными. Отличительной
особенностью этих рядов динамики представленных в абсолютных величинах является
возможность суммирования их уровней. Интервальные показатели могут быть просуммированы
для получения накопленного итога. Например, суммируя помесячную
реализацию, получаем как результат обще
годовую реализацию.
Сумма
уровней моментного ряда (табл. 3.1) не имеет смысла и накопленный итог для
таких рядов не рассчитывается.
Таблица 3.1
|
|
1993
|
1994
|
1995
|
1996
|
|
Число
зарегистрированных малых предприятий
|
218, 3
тыс.
|
356, 1
тыс.
|
419,4
тыс.
|
374, 6
тыс.
|
Для
анализа динамических рядов используют следующие показатели: абсолютный прирост
(или убыль), темп прироста (убыли), темп роста и абсолютное значение одного
процента прироста (убыли) (см. табл. 3.2).
1. Абсолютный прирост - разность уровней данного года и
предыдущего. Например (по данным табл. 2), для
II кв. 44,6 - 39,8 = + 4,8.
2. Темп прироста - процентное отношение абсолютного прироста
к предыдущему уровню. Например, для II кв.: 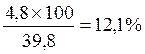
3.
Темп роста - процентное отношение последующего уровня к предыдущему уровню. Например,
для II кв.: 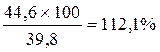
Таблица 3.2
Время вынужденного простоя рабочих завода за I – IV кварталы (часы
на 100 среднесписочных рабочих)
|
Показатели
|
I
кв.
|
II
кв.
|
III
кв.
|
IV
кв.
|
Итого
за год
|
|
Число часов на 100 рабочих
|
39,8
|
44,6
|
55,5
|
59,7
|
-
|
|
Абсолютный прирост
|
-
|
+4,8
|
+10,9
|
+4,2
|
+19,9
|
|
Темп прироста
|
-
|
+12,1
|
+24,4
|
+7,5
|
+50,0
|
|
Темп роста
|
-
|
112,1
|
124,4
|
107,5
|
150,0
|
Используя
статистический метод для характеристики динамических рядов, следует всегда
исходить из необходимости предварительного качественного анализа сущности
изучаемого явления. Без этого не может быть осмыслена статистика динамических рядов.
Динамический ряд не
всегда состоит из уровней, последовательно изменяющихся в сторону снижения или
увеличения. Нередко некоторые уровни в динамическом ряду представляют
значительные колебания, что затрудняет возможность проследить основную
закономерность, свойственную явлению в наблюдаемый период, а значит и
спрогнозировать явление на будущие периоды.
В этих случаях для выявления общей динамической тенденции рекомендуется
произвести выравнивание ряда.
Выявление основной тенденции развития
(тренда) называется выравниванием временного ряда, а методы выявления основной
тенденции – методами выравнивания.
Существует несколько способов выравнивания
динамического ряда: укрупнение интервала, сглаживание ряда при помощи групповой
и скользящей средней и другие. Однако выравнивание уровней динамических рядов
необходимо осуществлять только после глубокого и всестороннего анализа причин,
обусловивших колебания этих уровней. Механическое выравнивание может
искусственно сгладить уровни и завуалировать причинно-следственные связи.
Метод укрупнение
интервала. Укрупнение интервала
производят путем суммирования данных за ряд смежных периодов. Смысл приема
заключается в том, что первоначальный ряд динамики преобразуется и заменяется
другим, показатели которого относятся к большим по продолжительности периодам.
Вновь образованный ряд может содержать либо абсолютные величины за укрупненные
по продолжительности периоды времени (эти величины получаются путем простого
суммирования уровне первоначального ряда абсолютных величин), либо средние
величины. При суммировании уровней или при выведении средних по укрупненным
интервалам отклонения в уровнях, обусловленные случайными причинами,
взаимопогашаются, сглаживаются и более четко обнаруживается действие основных
факторов изменения уровней (общая тенденция).
Вычисление групповой
средней для каждого укрупнённого периода производят следующим образом:
суммируют смежные уровни соседних периодов, а затем полученную сумму делят на
число слагаемых (табл. 3.3). Для уровней динамического ряда, представленных в
табл.3.3, характерны волнообразные колебания. Выравнивание ряда путем
вычисления групповой средней позволило получить данные, иллюстрирующие довольно
четкую тенденцию к постепенному снижению процента расхождений уровней динамического
ряда.
Таблица 3.3
Динамика
процента выпуска некондиционной продукции по данным предприятия А за 1988-1995
годы
|
Годы
|
1988
|
1989
|
1990
|
1991
|
1992
|
1993
|
1994
|
1995
|
|
Процент
выпуска
|
11,0
|
9,8
|
8,0
|
9,2
|
8,2
|
8,6
|
8,5
|
7,9
|
|
Групповая
средняя
|
10,4
|
8,6
|
8,4
|
8,2
|
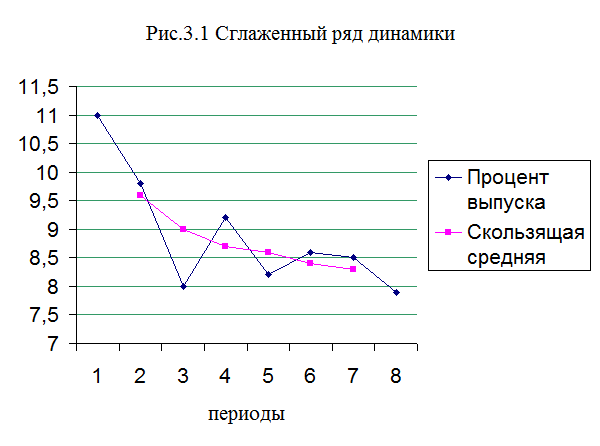
Метод скользящей
средней. Вычисление скользящей
средней позволяет каждый уровень заменить на среднюю величину из данного уровня
и двух соседних с ним (табл. 3.4). Каждый последующий интервал получаем,
постепенно сдвигаясь от начального уровня динамического ряда на один уровень.
Тогда первый интервал будет включать уровни
х1, х2, …хn; второй
– уровни х2, х3, …хn+1 и
т.д. Таким образом, интервал сглаживания как бы скользит по динамическому ряду
с шагом, равным единице. По сформированным укрупненным интервалам определяется
сумма значений уровней, на основе которых рассчитывают скользящие средние.
Полученная средняя относится к середине укрупненного интервала. Таким образом,
скользящая средняя является простейшим способом выравнивания ряда. Этот метод
дает возможность сгладить, устранить резкие колебания динамического ряда.
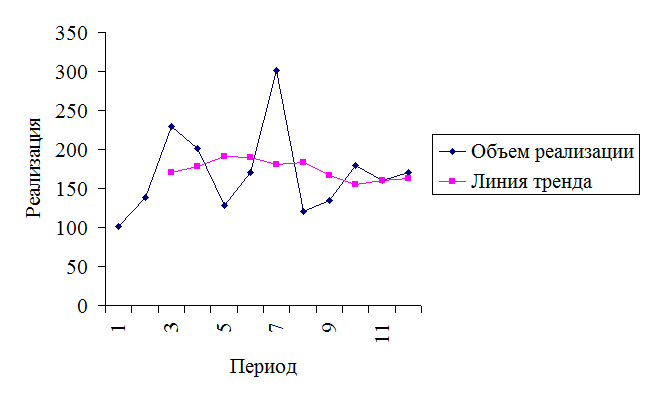
Пример расчета скользящей средней представлен в таблице 3.4 и на рис.3.1.
Таблица 3.4
|
Годы
|
1988
|
1989
|
1990
|
1991
|
1992
|
1993
|
1994
|
1995
|
|
Периоды
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
Процент
выпуска
|
11,0
|
9,8
|
8,0
|
9,2
|
8,2
|
8,6
|
8,5
|
7,9
|
|
Скользящая
средняя
|
-
|
9,6
|
9,0
|
8,7
|
8,6
|
8,4
|
8,3
|
-
|
Порядок
расчета: для 1989 года (11,0 + 9,8 + 8,0) : 3 = 9,6;
для
1990 года (9,8 + 8,0 + 9,2) : 3 = 9,0 и т. д.
Изучение основной
тенденции развития методом скользящей средней является лишь эмпирическим
приемом предварительного анализа. Рассмотренные приемы сглаживания динамических
рядов (укрупнение интервала и метод скользящей средней) могут рассматриваться
как упрощенный вариант анализа. В условиях повышенной неопределенности внешней
среды невозможно с большой вероятностью оценить то или иное влияние параметров
рынка на показатели, интересующие предприятия при прогнозировании деятельности.
Также существует проблема достоверности информации – точность определения
уровней ряда (например, по реальным доходам группы потребителей). Поэтому,
достаточно часто при анализе тенденций часто ограничиваются двумя
вышеперечисленными методами. Более строгим методом выявления тенденций является
метод аналитического выравнивания динамического ряда.
Метод аналитического
выравнивания динамического ряда.
Основным содержанием метода аналитического выравнивания рядов динамики является
расчет общей тенденции развития как функции времени. Основным содержанием
метода аналитического выравнивания рядов динамики является расчет общей
тенденции развития как функции времени. В этом случае фактические уровни
заменяются уровнями, вычисленными на основе определенной кривой.
Предполагается, что она отражает общую тенденцию изменения во времени изучаемого
показателя. При аналитическом выравнивании закономерно изменяющийся уровень
изучаемого показателя оценивается как функция времени
yt2 = f(t), где yt2
– уровни динамического
ряда, вычисленные по соответствующему аналитическому уравнению на момент времени
t.
Определение
теоретических (расчетных) уровней yt2 производится
на основе так называемой адекватной математической модели, которая наилучшим
образом отображает основную тенденцию развития ряда динамики.
Простейшими моделями
(формулами), выражающими тенденцию развития, являются следующие:
линейная
функция - прямая 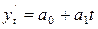
показательная
функция 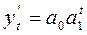
степенная
функция - кривая второго порядка (парабола)
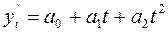
Выбор формы кривой во
многом определяет результаты экстраполяции
тренда. Экстраполяция – это продление в будущем тенденции,
наблюдавшейся в прошлом. Основанием для выбора кривой может служить
содержательный анализ сущности развития данного явления. Можно опираться также
на результаты предыдущих исследований в данной области.
Выравнивание по прямой
используется в тех случаях, когда абсолютные приросты практически постоянны,
т.е. когда уровни изменяются в арифметической прогрессии (или близко к ней).
Выравнивание по показательной функции используется в тех случаях, когда ряд
отражает развитие в геометрической прогрессии, т.е. цепные коэффициенты роста
практически постоянны. Выравнивание по степенной функции (параболе второго
порядка) используется в случае, если ряды динамики изменяются с постоянными цепными
темпами прироста.
Расчет параметров
функции обычно производится методом наименьших квадратов (МНК). В качестве
решения принимается точка минимума суммы квадратов отклонений между
теоретическим и эмпирическим уровнями:
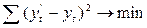
где: yt2 -
выровненные ( расчетные) уровни;
yt - фактические
уровни.
Параметры уравнения ai, удовлетворяющие этому условию, могут быть найдены
решением системы нормальных уравнений. На основе найденного уравнения тренда
вычисляются выровненные уровни. Нормальные уравнения МНК имеют вид:
для линейного тренда:
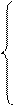
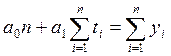
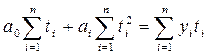
для параболы второго
порядка:
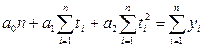
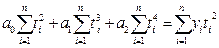
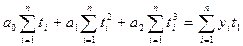
где: yi -
уровни исходного ряда динамики;
ti -
номера периодов или моментов времени (1,2,3:n);
n - число уровней ряда;
а0, а1, а2
- константы уравнений.
Для решения систем
уравнений обычно применяется способ определителей или способ отсчета от
условного начала. Для упрощения расчетов удобнее воспользоваться способом
отсчета от условного начала. При этом сумма показателей времени изучаемого ряда
динамики должна быть равна нулю:
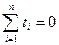
При нечетном числе
уровней ряда динамики уровень, находящийся в середине ряда, принимается за
условное начало отсчета времени (этому периоду или моменту времени придается
нулевое значение). Даты времени, стоящие выше этого уровня, обозначаются натуральными
числами со знаком минус (-1, -2, -3 и т.д.), а ниже - натуральными числами со
знаком плюс (+1, +2, +3 и т.д.).
Если число уровней
динамического ряда четное, периоды времени верхней половины ряда (до середины)
нумеруются -1, -2, -3 и т.д., а нижней - +1, +2, +3 и т.д. При этом условие
системы нормальных уравнений преобразуются следующим образом:
для линейного тренда:
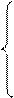
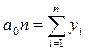
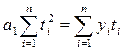
для параболы второго
порядка:
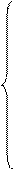
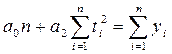
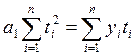
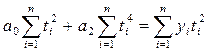
По вычисленным
параметрам производятся синтезирование трендовой модели функции, то есть
полученных значений а0, а1, а2 , и их
подстановка в искомое уравнение. Правильность расчетов аналитических уровней
можно проверить по следующему условию - сумма значений эмпирического ряда
должна совпадать с суммой вычисленных уровней выровненного ряда. При этом может
возникнуть небольшая погрешность в расчетах из-за округлений вычисляемых величин.
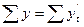
Для анализа
адекватности полученной зависимости используются различные критерии. Один из
них - стандартизированная ошибка аппроксимации - 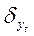 :
:
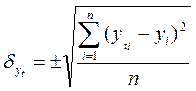
где 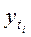 - теоретические уровни;
- теоретические уровни;
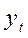 - экспериментальные уровни;
- экспериментальные уровни;
n - число уровней ряда.
За наиболее адекватную
принимается та функция (модель), у которой 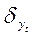 минимальная.
минимальная.
После выбора наиболее
адекватной модели можно сделать прогноз на любой из периодов. При составлении
прогнозов оперируют не точечной, а интервальной оценкой, определяя так
называемые доверительные интервалы прогноза. Величина доверительного интервала
определяется в общем виде следующим образом:
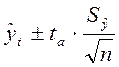
где 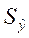 - среднее
квадратическое отклонение от тренда;
- среднее
квадратическое отклонение от тренда;
ta
- табличное значение
t-критерия Стьюдента при уровне значимости a. Зависит от уровня
значимости a (%) и числа степеней свободы k=n-m.
Величина 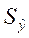 определяется по
формуле
определяется по
формуле
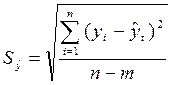
где:
yi и 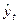 - соответственно фактические и расчетные значения уровней
динамического ряда;
- соответственно фактические и расчетные значения уровней
динамического ряда;
n - число уровней ряда;
m - количество
параметров в уравнении тренда (для уравнения прямой m=2, для уравнения параболы
2-го порядка m=3).
После проведения
необходимых расчетов определяется интервал, в котором с определенной
вероятностью будет находиться прогнозируемая величина. Пример метода
аналитического выравнивания динамического ряда представлен в таблице 3.5.
Предположим, что имеются данные о реализации за три года: 1995, 1996 и 1997.
Требуется сделать прогноз на 1998 год.
Графическое изображение объема реализации близко по форме к линейной
зависимости. Поэтому, рассмотрим случай линейного тренда 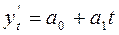
Таблица 3.5
|
год
|
Квартал
|
Номер
периода, t
|
Объем
реализации, y
|
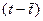
|
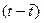 2 2
|
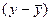
|
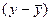 х х 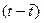
|
|
1995
|
I
|
1
|
102
|
-5,5
|
30,25
|
-69,25
|
380,875
|
|
|
II
|
2
|
140
|
-4,5
|
20,25
|
-31,25
|
140,625
|
|
|
III
|
3
|
235
|
-3,5
|
12,25
|
63,75
|
-223,125
|
|
|
IV
|
4
|
120
|
-2,5
|
6,25
|
-51,25
|
128,125
|
|
1996
|
I
|
5
|
118
|
-1,5
|
2,25
|
-53,25
|
79,875
|
|
|
II
|
6
|
150
|
-0,5
|
0,25
|
-21,25
|
10,625
|
|
|
III
|
7
|
270
|
0,5
|
0,25
|
98,75
|
49,375
|
|
|
IV
|
8
|
140
|
1,5
|
2,25
|
-31,25
|
-46,875
|
|
1997
|
I
|
9
|
135
|
2,5
|
6,25
|
-36,25
|
-90,625
|
|
|
II
|
10
|
185
|
3,5
|
12,25
|
13,75
|
48,125
|
|
|
III
|
11
|
290
|
4,5
|
20,25
|
118,75
|
534,375
|
|
|
IV
|
12
|
170
|
5,5
|
30,25
|
-1,25
|
-6,875
|
|
|
|
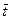 = 6,5 = 6,5
|
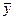 = 171,25 = 171,25
|
|
143
|
|
1004,5
|
Примечание:
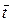 - среднее значение периода за наблюдаемый период;
- среднее значение периода за наблюдаемый период;
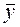 - среднее значение реализации за наблюдаемый период
- среднее значение реализации за наблюдаемый период
Формулы
для определения коэффициентов тренда:
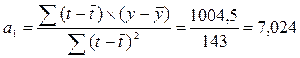
Для
значения прогноза на период t : 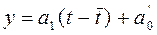
где: 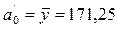
Окончательная
аналитическая формула прогноза будет иметь следующий вид:
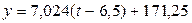 или
или 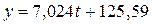
Прогноз
на 1998 год: 1 квартал: 7,024 х 13 + 125,59 = 216,9
2 квартал:
7,024 х 14 + 125,59 = 223,9 и т.д.
Динамические ряды
экономических показателей часто имеют небольшую длину и подвержены значительным
колебаниям, которые аппроксимация предвидеть не может. Поэтому в практике
статистического анализа экономических параметров достаточно часто используют
метод адаптивного моделирования и прогнозирования.
2. Метод адаптивного прогнозирования
В основе адаптивных
методов лежит модель экспоненциального сглаживания. Сущность этого
метода заключается в том, что временной ряд сглаживается с помощью взвешенной
скользящей средней, в которой веса распределяются по экспоненциальному закону.
Экспоненциальное сглаживание - это очень популярный
метод прогнозирования многих временных рядов.
Простая и прагматически
ясная модель временного ряда имеет следующий вид: Xt = b + et,
где b - константа и e - случайная ошибка.
Константа b относительно стабильна на каждом временном
интервале, но может также медленно изменяться со временем. Один из интуитивно
ясных способов выделения b состоит в том,
чтобы использовать сглаживание скользящим средним, в котором последним
наблюдениям приписываются большие веса, чем предпоследним, предпоследним
большие веса, чем пред-предпоследним и т.д. Простое экспоненциальное именно так
и устроено. Здесь более старым наблюдениям приписываются экспоненциально
убывающие веса, при этом, в отличие от скользящего среднего, учитываются все
предшествующие наблюдения ряда, а не те, что попали в определенное окно. Точная формула простого экспоненциального сглаживания имеет
следующий вид: 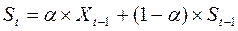
где:
Xt-1
– наблюдаемое значение в предшествующий период;
St-1
– прогнозное значение предыдущего периода;
a
- константа сглаживания
Когда эта формула применяется
рекурсивно, то каждое новое сглаженное значение (которое является также
прогнозом) вычисляется как взвешенное среднее текущего наблюдения и сглаженного
ряда. Очевидно, результат сглаживания зависит от параметра a. Если a равно 1, то предыдущие
наблюдения полностью игнорируются. Если a равно 0, то
игнорируются текущие наблюдения. Значения a между 0 ¸ 1 дают промежуточные результаты. Эмпирические
исследования показали, что весьма часто простое экспоненциальное сглаживание
дает достаточно точный прогноз.
Предположим, что
имеются наблюдения за четыре периода времени. Прогнозное значение на пятый
период времени может быть представлено как: S5
= aX4
+ (1-a)
S4
При этом следует
учесть, что прогнозное значение в предыдущий период было, в свою очередь, определено на основе
предыдущих наблюдений. Этот процесс можно представить следующим образом:
St-1
= aXt-2 + (1-a) St-2
St-2
= aXt-3 + (1-a) St-3
St-3
= aXt-4 + (1-a) St-4
Если
подставить три формулы в выражение для St, то получим:
St = aXt-1
+ a (1-a) Xt-2
+ a (1-a)2 Xt-3
+ a (1-a)3 Xt-4
+ (1-a)4 St-4
Для того чтобы
вычислить St
необходимо определить St-4.
Обычно полагают, что первое прогнозное значение совпадает с первым наблюдаемым значением, то есть
для рассматриваемого случая принимаем St-4
= Xt-4
Расчет прогнозного
значения также можно представить в несколько другом виде: St = St-1+ a (Xt-4 - St-1)
Дальнейший прогноз
зависит от значения коэффициента a. Выбор коэффициента a производится теоретическим и эмпирическим способом.
Поиск на сетке. Возможные
значения параметра разбиваются сеткой с определенным шагом. Например,
рассматривается сетка значений от a = 0,1 до a = 0,9, с шагом 0,1. Затем выбирается a, для которого сумма квадратов (или средних
квадратов) остатков (наблюдаемые значения минус прогнозы на шаг вперед)
является минимальной.
Индексы
качества подгонки. Самый прямой способ оценки прогноза, полученного на
основе определенного значения a - построить график наблюдаемых значений и прогнозов
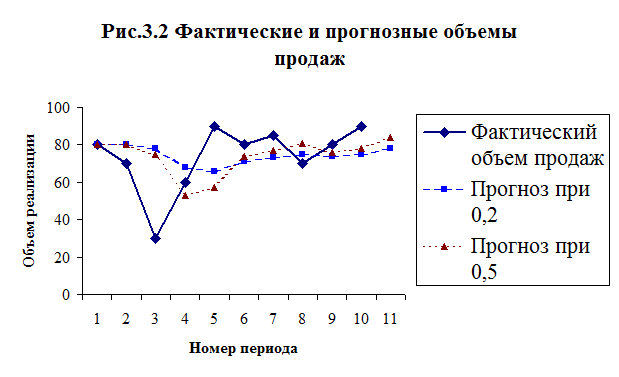
на один шаг вперед (см.рис.3.2 и 3.3). Этот график включает в себя также
остатки (отложенные на правой оси Y). Из графика ясно видно, на каких
участках прогноз лучше или хуже. Такая визуальная проверка точности прогноза
часто дает наилучшие результаты. Имеются также другие меры ошибки, которые
можно использовать для определения оптимального параметра a.
Эмпирический
выбор. Как было указано
выше, значение коэффициента a находится в
диапазоне 0 ¸1. Если значение a близко к нулю, то это означает, что для расчета
нового прогнозного значения достаточно ввести небольшие коррективы. Такой
подход к построению прогнозов возможен в тех случаях. Когда исходные данные
характеризуются невысокой изменчивостью. В тех случаях, когда наибольшие
значения для прогноза имеют самые последние наблюдаемые значения, следует
выбирать коэффициент близкий к 1. Но при больших значениях a прогнозные значения становятся слишком
чувствительны к «шуму» (случайным колебаниям) и достаточно сильно реагируют на
случайные совпадения данных в недавнем прошлом.
В таблице 3.6 и на
рисунке 3.2. представлены данные о реализации товара, определенного вида. Для
того чтобы продемонстрировать влияние на точность прогнозирования коэффициента a рассмотрим два его значения a = 0,2 и a = 0,5
Таблица
3.6
|
Номер периода
|
Фактический объем продаж (Х)
|
Прогнозный объем (S) при a = 0,2
|
Прогнозный объем (S) при a = 0,5
|
|
1
|
80
|
80
|
80
|
|
2
|
70
|
16 + 64 = 80*
|
40 + 40 = 80*
|
|
3
|
30
|
14 + 64 = 78
|
35 + 40 = 75
|
|
4
|
60
|
6 + 62 = 68
|
15 + 37,5 = 53
|
|
5
|
90
|
66
|
57
|
|
6
|
80
|
71
|
74
|
|
7
|
85
|
73
|
77
|
|
8
|
70
|
75
|
81
|
|
9
|
80
|
74
|
76
|
|
10
|
90
|
75
|
78
|
|
11
|
|
78
|
84
|
* расчет производится по формуле 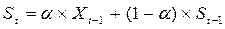
например: 0,2 х 80 +
0,8 х 80 = 16 + 64 = 80
0,2 х 70 + 0,8 х 80 = 14 + 64 = 78 и т.д.
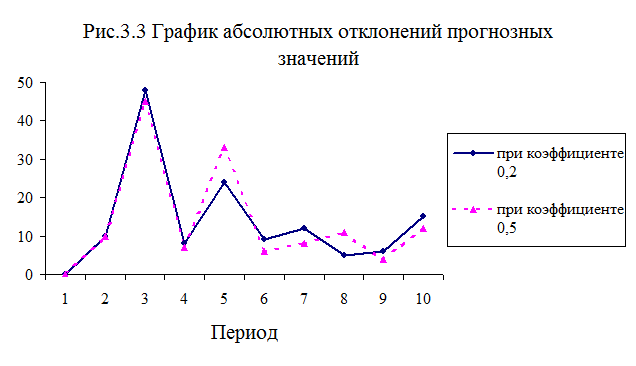 На графике абсолютных отклонений
прогнозных величин (см. рис. 3.3) заметно, что большие значения a обеспечивают приемлемую точность прогноза в тех
случаях, когда объем продаж в течение определенного времени изменяется в одном
направлении. В тех случаях, когда наблюдаются значительные колебания исходных
данных, большие значения a не обеспечивают высокую точность прогнозов.
На графике абсолютных отклонений
прогнозных величин (см. рис. 3.3) заметно, что большие значения a обеспечивают приемлемую точность прогноза в тех
случаях, когда объем продаж в течение определенного времени изменяется в одном
направлении. В тех случаях, когда наблюдаются значительные колебания исходных
данных, большие значения a не обеспечивают высокую точность прогнозов.
Кроме указанных выше,
существуют и другие методы определения коэффициента сглаживания a, но они являются достаточно сложными и подробно
описываются в специальной литературе.
3. Прогнозирование на основе сезонной модели с трендом
В дополнение к простому
экспоненциальному сглаживанию, были предложены более сложные модели, включающие
сезонную компоненту и трендом. Общая идея таких моделей состоит в том, что
прогнозы вычисляются не только по предыдущим наблюдениям (как в простом экспоненциальном
сглаживании), но и с некоторыми задержками, что позволяет независимо оценить
тренд и сезонную составляющую. Существуют различные модели сезонности - аддитивная
и мультипликативная сезонность и тренды - линейный тренд, экспоненциальный, демпфированный.
Аддитивная и мультипликативная
сезонность. Многие
временные ряды имеют сезонные компоненты. Например, какое либо явление имеет
пики или спады в определенные периоды. Эта периодичность имеет место каждый
год. Однако относительный размер наблюдаемого явления (например, продажи) может
слегка изменяться из года в год. Таким образом, имеет смысл независимо
экспоненциально сгладить сезонную компоненту.
Сезонные компоненты, по природе своей, могут
быть аддитивными или мультипликативными. Различие между двумя видами сезонности
состоит в том, что в аддитивной модели сезонные отклонения не зависят от
значений ряда, тогда как в мультипликативной модели величина сезонных
отклонений зависит от значений временного ряда.
Например, в течение
декабря продажи определенного вида товара увеличиваются на 1 миллион рублей
каждый год. Для того чтобы учесть сезонное колебание, добавляют в прогноз на
декабрь 1 миллион рублей (сверх соответствующего годового среднего). В этом
случае сезонность - аддитивная. Альтернативно, пусть в декабре продажи
увеличились на 40%, т.е. в 1.4 раза. В этом случае продажи увеличатся в
определенное число раз, и сезонность будет мультипликативной (в данном случае
мультипликативная сезонная составляющая равна 1.4).
Аддитивная модель:
прогноз t = St ± It-p
Мультипликативная
модель: прогноз t = St ´ It-p
В этой формуле St
обозначает (простое) экспоненциально сглаженное значение ряда в момент t,
и It-p обозначает сглаженный сезонный фактор в момент t
минус p (p - длина сезона). Таким образом, в сравнении с простым
экспоненциальным сглаживанием, прогноз "улучшается" добавлением или
умножением сезонной компоненты.
Рассмотрим пример
прогнозирования с учетом сезонной составляющей на базе тренда, построенного с
помощью метода скользящей средней (табл. 3.7 и рис. 3.4).
Таблица
3.7
|
Год
|
квартал
|
Порядковый номер
квартала
|
Товарооборот
|
Тренд
|
Сезонные отклонения
|
|
абс.
|
%
|
|
1997
|
I
|
1
|
101
|
|
|
|
|
II
|
2
|
138
|
|
|
|
|
III
|
3
|
230
|
170,875
|
59,125
|
134,601
|
|
IV
|
4
|
201
|
178,25
|
22,75
|
112,763
|
|
1998
|
I
|
5
|
128
|
191,125
|
-63,125
|
66,9719
|
|
II
|
6
|
170
|
189,875
|
-19,875
|
89,5326
|
|
III
|
7
|
301
|
180,625
|
120,375
|
166,644
|
|
IV
|
8
|
120
|
182,75
|
-62,75
|
65,6635
|
|
1999
|
I
|
9
|
135
|
166,375
|
-31,375
|
81,142
|
|
II
|
10
|
180
|
155
|
25
|
116,129
|
|
III
|
11
|
160
|
160,625
|
-0,625
|
99,6109
|
|
IV
|
12
|
170
|
163,125
|
6,875
|
104,215
|
Рис. 3.4. Прогнозирования с учетом сезонной
составляющей на базе тренда
 Аддитивная модель:
Аддитивная модель:
-
отклонения по 1
кварталам: -63,125; -31,375. Среднее отклонение составит (-63,125) + (-31,375)
/ 2 = - 47,25
-
отклонения по 2
кварталам: -19,875; 25. Среднее отклонение составит 2,56
-
отклонения по 3
кварталам: 59,125; 120,375; -0,625. Среднее отклонение составит 59,62
-
отклонения по 4
кварталам: 22,75; -62,75; 6,875. Среднее отклонение составит –11,04.
Мультипликативная модель: аналогично аддитивной модели определяются средние сезонные отклонения,
выраженные в процентах. Таким образом, для 1го квартала оно составит 74,056%;
для 2го квартала – 102,82%; для 3го
квартала – 133,6%; для 4го квартала – 94,21%.
Прогноз
на 2000 год определяется следующим образом (см.табл.3.8):
Таблица 3.8
|
Квартал 2000 года
|
Экстраполяция значения тренда *
|
Прогнозные значения объема реализации
с учетом сезонных отклонений
|
|
Аддитивная модель
|
Мультипликативная модель
|
|
I
|
163,125–0,86=162,265
|
162,265-47,25 =
115,015
|
163,125
х 74%=120,7
|
|
II
|
162,265-0,86=161,405
|
161,405+2,56 = 163,965
|
163,125
х 102,82%=167,7
|
|
III
|
161,405-0,86=160,545
|
160,545+59,62= 220,165
|
163,125
х 133,6%=217,93
|
|
IV
|
160,545-0,86=159,685
|
159,685–11,04 = 148,645
|
163,125
х 94,21%=153,66
|
*Примечание:
экстраполяция линии тренда производится с помощью константы, которая
определяется по формуле (163,125-170,875)/(12–3) = -
0,86
Для принятия
маркетинговых решений необходима информация о влиянии маркетинговых
инструментов на целевые показатели, а значит прогнозирование деятельности с их
применением. Статистика разработала множество методов изучения связей, выбор
которых зависит от целей исследования и от поставленных задач. Изучение зависимости
вариации признака от окружающих условий составляет содержание теории
корреляции.