КАФЕДРА  ЭКОНОМИКО-МАТЕМАТИЧЕСКИХ МЕТОДОВ И МОДЕЛЕЙ

А У Д И Т О Р Н А Я  Р А Б О Т А

по   дисциплине

Эконометрика

Вариант 5

Липецк

2006

Вариант 5

Изучается зависимость средней ожидаемой продолжительности жизни от нескольких факторов по данным за 1995 г., представлен­ным в табл.1.

                                                                                              Таблица 1

Принятые в таблице обозначения:

Y - средняя ожидаемая продолжительность жизни при рождении, лет;

X₁ - ВВП в паритетах покупательной способности;

X₂- цепные темпы прироста населения, %;

X₃- цепные темпы прироста рабочей силы, %;

Х₄ - коэффициент младенческой смертности, %..

Задание

1.           Постройте матрицу парных коэффициентов корреляции, оцените статистическую значимость  коэффициентов  корреляции. Устано­вите, какие факторы коллинеарны.

2.           Постройте уравнение множественной регрессии, обосновав отбор факторов.

3.           Постройте график остатков.

4.           Проверьте выполнение предпосылок  МНК.

5.           Оцените статистическую значимость уравнения множественной регрессии. Какие факторы значимо воздействуют на формирование средней ожидаемой продолжительности жизни в этом уравнении?

6.           Постройте уравнение множественной регрессии только со статистически значимыми факторами.

7.     Рассчитайте прогнозное значение результата, если прогнозные значения факторов составляют 80% от их максимальных значений.

8.     Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости 5 или 10% (а = 0,05; а = 0,10).

Решение.

Построение матрицы коэффициентов парной регрессии выполняется с помощью табличного процессора Excel (пакет Анализ данных→Корреляция). В результате получаем следующие данные:

                                                                           Таблица 2

Анализ матрицы коэффициентов парной корреляции:

- зависимая переменная y, т.е. средняя ожидаемая продолжительность жизни при рождении имеет тесную связь с ВВП в паритетах покупательной способности – х₁ (r_yx1=0,638668), с коэффициентом младенческой смертности – х₄ (r_yx4=-0,85288);

- факторы х₂ и х₃ коллинеарны, т.е. находятся в линейной зависимости между собой (r_x2x3=0,728064), но так как и фактор х₂ и фактор х₃ незначимы (r_yx2=-0,20745, r_yx3=0,283051), то нет смысла включать их в модель.

После исключения незначимых факторов получаем k=2, т.е. в модель включаем только два фактора.

Для построения уравнения множественной регрессии применим инструмент Регрессия (Анализ данных в Excel). Уравнение регрессии зависимости ожидаемой продолжительности жизни при рождении от ВВП в паритетах покупательной способности и коэффициента младенческой смертности можно записать в следующем виде:

         y=67,543+0,675х₁-0,186х₂.

В таблице 3 приведены вычисленные по модели значения Y и значения остаточной компоненты.

                                                                                Таблица 3

На рисунке 1 приведен график остатков.

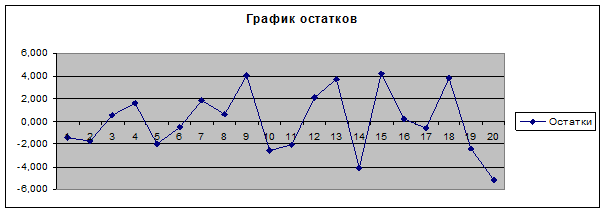
                                                                                                       Рис.1 

Исследование остатков предполагает проверку наличия следующих пяти предпосылок МНК:

         1. Случайный характер остатков. Т.к. на графике получена горизонтальная полоса, то остатки представляют собой случайные величины и МНК оправдан, теоретические значения y_расч хорошо аппроксимируют фактические значения y.

         2. Нулевая средняя величина остатков, не зависящая от  x_i.  ∑(y-y_расч)=0,  на рис.2 и рис.3 представлены графики зависимости случайных остатков от значений х_j, из которых видно, что ε_i независимы от х_j,   т.е. вторая предпосылка выполняется.

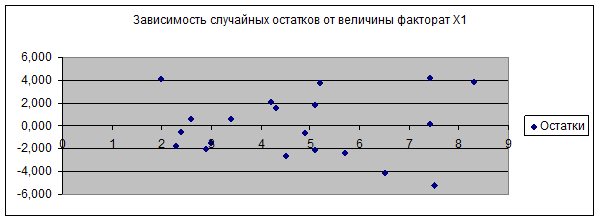
                                                                                                       Рис.2

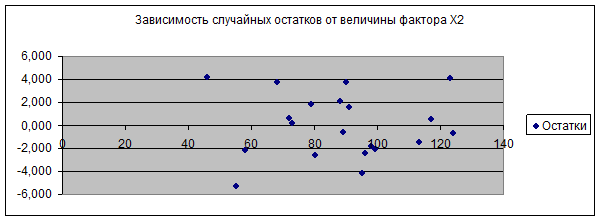
                                                                                                       Рис.3

         3. Гомоскедастичность – дисперсия каждого отклонения ε_i  одинакова для всех значений х. Наличие гомоскедастичности можно видеть на графике зависимости остатков от теоретических значений y_расч (р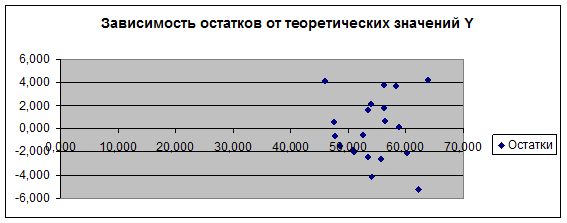ис.4).

                                                                                                                                  Рис.4

Для оценки гетероскедастичности используем метод Готфельда-Квандта. В таблице 4  приведены расчеты проверки регрессии на гетероскедастичность.                      

                                                                                        Таблица 4

Величина R=92,578/28,321=3,2689 не превышает табличное значение F-критерия, равного  5,409447, подтверждая тем самым наличие гомоскедастичности.

         4. Отсутствие автокорреляции остатков. Значения остатков распределены независимо друг от друга. Коэффициент корреляции между ε_i  и  ε_j, где ε_i – остатки текущих наблюдений, ε_j – остатки предыдущих наблюдений, может быть определен как

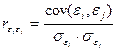                   =0,264145,

что при 17 степенях свободы явно незначимо, т.е. можно           сказать, что автокорреляция остаточных величин отсутствует.

         5. Остатки подчиняются нормальному распределению. Предпосылка о нормальном распределении остатков позволяет проводить проверку параметров регрессии и корреляции с помощью критериев t, F.

         Оценим качество всего уравнения регрессии. Значения коэффициентов детерминации можно найти в таблице Регрессионная статистика (таблица 4).

                                                                           Таблица 4

Коэффициент детерминации:        

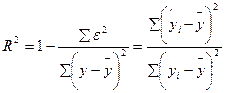         =0,76175.

Коэффициент детерминации  характеризует долю вариации результативного признака y под воздействием изучаемых факторов. Следовательно, около 84% вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов.

Коэффициент множественной корреляции R:

         0,872783.

Он показывает тесноту связи зависимой переменной Y с двумя включенными в модель объясняющими факторами.

Оценку статистической значимости уравнения регрессии произведем на основе вычисления F-критерия Фишера:

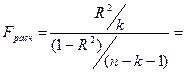         21,17676

В Excel значение F-критерия можно найти в таблице Дисперсионный анализ (табл. 5).

                                                                                           Таблица 5

Рассчитанные значения F_расч сравниваем с табличным значением F_табл. В Excel F_табл при доверительной вероятности 0,95 при ν₁=k=2 и ν₂=n-k-1=20-2-1=17 находим при помощи функции FРАСПОБР:

         F_табл=3,591538.

Уравнение регрессии с вероятностью 0.95 в целом статистически значимое, т.к. F_расч> F_табл.

Статистическую значимость коэффициентов уравнения множественной регрессии оцениваем с помощью t-критерия Стьюдента:

         t_aj=a_j / S_aj,

         S_aj=S_ε ,

где  b_jj – диагональный элемент матрицы (Х^ТХ)^-1.

         t_a0 =14,288

         t_a1 =1,565

         t_a2 =-5,025

                                                                                     Таблица 6

Расчетные значения t-критерия Стьюдента для коэффициентов уравнения регрессии а₁, а₂ приведены в четвертом столбце таблицы 6. Критическое значение t_табл при α=0,05 и степенях свободы (20-2-1=17) находим в Еxcel с помощью функции СТЬЮДРАСПОБР.

         t_табл=2,109819.

Т.к. |t_a2|> t_табл, то коэффициент а₂ существенный (значим). Но |t_a1|< t_табл, следовательно коэффициент а₁ не значим.

Уравнение регрессии только со статистически значимыми факторами будет иметь вид:

         y=267,55-3,3121x.

Для выполнения прогноза среднего значения показателя y при х_прогн=0,8*х_i^max  используем линейную модель, полученную только со статистически значимыми факторами, для чего необходимо подставить прогнозируемое значение х в уравнение регрессии:

         y=73,56-0,2196x.

         х_прогн=99,2.

         Y_прогн= 73,56-0,2196*99,2=51,78

Вероятность реализации точечного прогноза практически равна нулю. Поэтому рассчитывается средняя ошибка прогноза или доверительный интервал прогноза с достаточно большой надежностью. Расчетные данные для выполнения интервального прогноза приведены в таблице 7.

                                                                                     Таблица 7

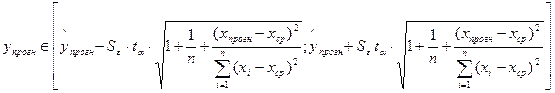
         =3,024907

         t_α=0,05=2,100924

Таким образом, прогнозное значение  ,будет находиться в интервале [45,22;58,34]. Все результаты моделирования и исходные данные приведены на графике (рис.5).

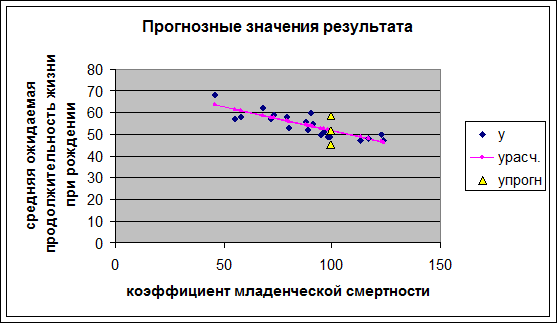
                                                                                                                      Рис.5