Имеются данные 15%-ного механического отбора ресторанов города по величине издержек обращения и производства (млн.руб.);

Таблица 1.1.

1.                На основе приведенных данных произвести группировку ресторанов города по величине издержек обращения и производства, выделив 5 групп с равными интервалами.

2.                На основе группировки следует:

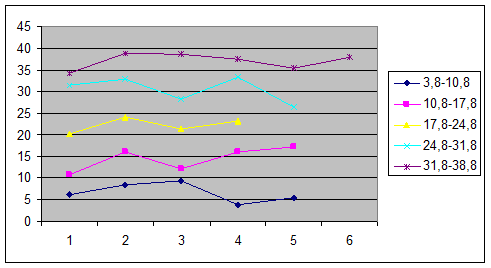
1)                построенный ряд распределения изобразить графически;

2)                определить среднюю величину издержек обращения и производства обследованных ресторанов города;

3)                определить модальную величину издержек обращения и производства ресторанов;

4)                рассчитать показатели вариации издержек обращения и производства.

3.                На основе показателей выборочной совокупности (обследованных ресторанов) рассчитать для генеральной совокупности (всех ресторанов города);

1)                с вероятностью 0,954 возможные значения средней величины издержек обращения и производства в ресторанах.

2)                С вероятностью 0,683 возможные значения доли ресторанов города имеющих величину издержек обращения и производства более 31,8 млн.руб.

Решение

Таблица 1.2.

Среднее арифметическое.

Хср = ∑Хi/n

Где хi – число

n – количество чисел

Хср =569/25 = 22,76

Мода

Мо = х_мо+i_мо*f_mo-f_mo-1/( f_mo-f_mo-1)+( f_mo-f_mo+1)

Где хмо- нижняя граница модального интервала, imo – величина модального интервала. -f_mo-1,f_mo,f_mo+1 – частоты соответственно модального, домодального и послемодального интервалов.

Если множество данных не содержит одинаковых данных, то функция МОДА возвращает значение ошибки #Н/Д

Мо =#Н/Д

Среднее квадратическое отклонение

σ = 1/n∑х-хср

σ =10,0896

Коэффициент вариации.

σ/х_ср *100

Коэффициент вариации = 44,33

На основе показателей выборочной совокупности (обследованных ресторанов) рассчитать для генеральной совокупности (всех ресторанов города);

Таблица 1.3.

Задача 2

Реализация кондитерских изделий в магазинах города характеризуется показательно следующими данными

Таблица 2.1.

На основе приведенных данных необходимо

1) рассчитать среднеквартальные уровни реализации кондитерских изделий, определить общий характер тенденции продажи на 1997-2001 гг.

2) исчертить сезонные колебания реализации кондитерских изделий

3) сезонную волну изобразить графически.

4) рассчитать объем реализации кондитерских изделий  за каждый год

5) на основе данных п.4 рассчитать базисные абсолютные приросты цепные темпы роста, среднегодовой абсолютный прирост кондитерских изделий 1997-2001 гг.

6) сделать прогноз объема реализации кондитерских изделий  на 1996 гг.

7) использую рассчитанные индексы сезонности сделать прогноз реализации кондитерских изделий по кварталам на 2003 г.

Решение

Таблица 2.2.

Задача 3.

Имеются данные о производстве с/х продукции по районам области:

Таблица 3.1.

Определить:

1) Индексы товарооборота в действующих и сопоставляемых ценах на основе

данных 1999 -2000г.г.;

2) изменение объема произведенной с/х продукции в целом и за счет действия

Различных факторов( в стоимости выражении) 2000г, по сравнению с 1999г.;

3) индивидуальные индексы цен индексы цен  постоянного и переменного состава на основе за 1999 и 2001г.

4) как повлияло изменение структуры производства с/х продукции на средние цены ( в абсолютных и относительных величинах);

5) как изменились средние цены на произведенную с/х продукцию в 2001 г. По сравнению 1999г.(в относительных величинах).

Решение

Таблица 3.2.

Задача 4.

Получены данные о стаже работы и нормах выработки 20 работников универмага:

Таблица 4.1.

На основе приведенных данных необходимо:

1)                установить зависимость между стажем работы и выполнением норм выработки, определить форму связи;

2)                выбрав соответствующее уравнение связи, рассчитать его параметры;

3)                вычислить показатель тесноты связи-индекс корреляции;

4)                используя теоретическое уравнение регрессии, сделать прогноз возможного %-ного выполнения норм выработки рабочим, имеющим стаж работы 8 лет.

Решение

Таблица 4.2.

Индекс корреляции = 0,46

используя теоретическое уравнение регрессии, сделать прогноз возможного %-ного выполнения норм выработки рабочим, имеющим стаж работы 8 лет.

Прогноз = 8/0,0359 = 222,65%

Задача 5.

На первое января текущего года  в крае насчитывалось 150000 детей в возрасте до 1 года, 151000 детей в возрасте 2 лет и 152000 детей в возрасте 3 лет.

Коэффициенты дожития до следующего возраста равны: для однолетних- 0,9950;для двухлетних – 0,9976;для трехлетних – 0,9988.

Определить: какой будет численность детей в возрасте 3-5 лет через три года.

Решение

Детей при 1 летнем = 150000*0,995 = 149250 детей.

Детей до 2 летнем = 151000*0,9976 = 150638 детей.

Всего детей в возрасте 3-5 лет = 149250 + 150638 = 299888 детей.

Задача 6.

По данным бухгалтерского и статистического учета акционерного промышленного предприятия за год известно.

Товарная продукция составила 655 млн.руб. Остатки полуфабрикатов на начало года - 18 млн.руб, на конец года -12 млн.руб., и течение года произведено полуфабрикатов на 606 млн.руб.из них использовано в других цехах предприятия на производство промышленной продукции на 280 млн.руб. Остатками незавершенного производства на конец увеличились по сравнению  с остатком на начало года на 15 млн.руб., остатки готовой продукции на складе увеличились на 9 млн.руб., а задолженность покупателю за отгруженную им продукцию снизилась на 3 млн.руб.

Определить:

1.   Валовую, готовую, отгруженную и реализованную продукцию акционерного промышленного предприятия за год.

2.   Показать взаимосвязь между исчисленными стоимостями показателей объема продукции.

Решение

Валовая продукция = 655+18-12+606 = 1267 млн.руб.

Готовая продукция = 1267 – 9 = 1258 млн.руб.

Отгруженная продукция = 1258-3 = 1255 млн.руб.

Реализованная продукция = 1255-15 = 1240 млн.руб.

Задача 7.

Имеются данные по двум шахтам:

Таблица 7.1.

Определить:

1.                Индексы производительности труда на каждой шахте и отдельности.

2.                Изменение средней( по двум шахтам) производительности труда.

3.                Какие факторы и в какой степени вызвали изменение средней производительности труда? Объяснить смысл каждого индекса.

Решение

Таблица 7.2.

Задача 8.

Имеются данные о себестоимости товарной продукции промышленного предприятия.

Таблица 8.1.

Определить:

1.                затраты на рубль товарной продукции по плану и фактически;

2.                Абсолютное и относительное изменение затрат на 1 рубль товарной продукции в целом и раздельно под влиянием изменения: а)ассортимента продукции. б)себестоимости. в) отпускных цен.

3.                Сделайте выводы.

Решение

Таблица 8.2.

Задача 9.

Имеются данные по акционерному предприятию в млн.руб.

Таблица 9.1.

Определить;

1.                За каждый год коэффициенты закрепления оборотных средств, скорость оборачиваемости (число оборотов) и продолжительности оборота в днях:

2.                Суммовой эффект от изменения оборачиваемости оборотных средств;

3.                Изменение размера оборотных средств в целом и раздельно за счет изменения оборачиваемости и объема реализации.

Решение

Таблица 9.2.

Задача 10.

Имеются следующие условные данные по предприятию за месяц, млн.руб.;

Выручка от реализации продукции                          1490

в том числе налог на добавленную стоимость          300

Себестоимость реализованной продукции                 974

Коммерческие и управленческие расходы                190

Получены чистые проценты                                        0,2

Чистые доходы от прочих операций (валовые доходы минус валовые расходы)                                                        20

Прочие внереализационные доходы                            11

Прочие внереализационные расходы                             9

Уплачен налог на прибыль                                            28

Чрезвычайные расходы                                                  19

Определить

1)                прибыль от реализации продукции;

2)                прибыль от финансово-хозяйственной деятельности;

3)                нераспределенную прибыль.

Решение

прибыль от реализации продукции = 1490 – 300 -974-190 = 26 млн.руб.

прибыль от финансово-хозяйственной деятельности = 26+0,2+20+11-9-28-19 = 20,2 млн.руб.

нераспределенную прибыль = 20,2-19 = 1,2 млн.руб.

Задача 11.

Результаты работы страховых организаций в 1 полугодии характеризуются следующими данными:

Таблица 11.1.

Определите:

1.средний коэффициент выплат

2.абсолютную сумму дохода страховых операций

3.относительную доходность.

Решение

Таблица 11.2.

средний коэффициент выплат = 640/1600 = 0,4

абсолютную сумму дохода страховых операций = 1600-640 = 960 млн.руб.

относительную доходность = 960/1600 *100 = 60% 

Задача 12.

Имеются следующие данные о краткосрочном кредитовании банками промышленных предприятий (млн.руб.);

Таблица 12.1.

Определите индексы средней длительности пользовании кредитом переменного, постоянного состава, структурных сдвигов.

Решение

Индекс среднего переменного состава

I пер = ∑х₁*f₁/∑f₁ : ∑x₀*f₀∑f₀

х₁,х₀ – время погашения в отчетном и базисном период периоде по каждой группе

f₁,f₀ – однодневный оборот по погашению кредита по каждой группе

Индекс среднего постоянного состава

I пост. = ∑х₁*f₁/∑ x₀*f₁

х₁,х₀ – время погашения в отчетном и базисном период периоде по каждой группе

f₁,f₀ – однодневный оборот по погашению кредита по каждой группе

Индекс структурных сдвигов

I стр. = ∑х₀*f₁/∑f₁ : ∑x₀*f₀∑f₀

х₁,х₀ – время погашения в отчетном и базисном период периоде по каждой группе

f₁,f₀ – однодневный оборот по погашению кредита по каждой группе

Таблица 12.2.

Индекс среднего переменного состава

I пер = 32,8/0,8 : 30/0,64 = 0,87

Индекс среднего постоянного состава

I пост. = 32,8/37,88 = 0,86

Индекс структурных сдвигов

I стр. = 37,88/0,8 :30/0,64 = 1,01

Вывод из проведенных расчетов видно, что индекс структурных сдвигов составляет 1,01 индекс среднего постоянного состава составляет 0,86, индекс среднего переменного состава 0,87

Список литературы

1.     Национальное счетоводство: Учебник / Под ред. Б. И. Башкатова. - 2-е издание. перераб. и доп. - М.: Финансы и статистика, 2002.

2.     Национальные счета в переходный период. - М.: Госкомстат России, 1994. – с. 63

3.     Экономическая статистика: Учебник. 2-е изд.. доп. / Под ред. Иванова Ю. Н. — М.: ИНФРА-М, 2002.

4.     Макроэкономическая статистика: Учеб. пособие / Салин В. Н., Медведев В Г. к др. -М. : Дело. 2001.

5.     Башкатов Б.И. Социально-экономическая статистика – М.: ЮНИТИ-ДАНА 2002. – 703 с.

6.     Боярский А.Я., Громыко Г.Л. “Общая теория статистики” М.: изд. Московские университеты, 1985 г. – 372 с.

7.     Васильева Э.К. “Социально-демографический портрет студента” М.: Мысль, 1986 г. – 96 с.

8.     Кильдишев и др. “Статистика населения с основами демографии” М.: Финансы и Статистика, 1990 г. – 312с.