Задание 1.  Предприятия района (номер предприятия Х) упорядочены по объему выпускаемой продукции. Показатель У характеризует численность управленческого персонала. Данные сведены в таблицу. По данным таблицы рассчитать коэффициенты линейной регрессии.

Х

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

У

2

2

2

2

2

2

2

2

2

2

3

3

3

3

3

Х

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

У

4

4

4

4

4

4

4

4

4

5

5

5

5

5

5

Решение:

Уравнение линейной регрессии имеет вид:   

,   где  ,  

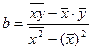Для проведения необходимых вычислений составим вспомогательную таблицу:

Х

У

Х∙Х

Х∙У

У∙У

1

2

1

2

4

2

2

4

4

4

3

2

9

6

4

4

2

16

8

4

5

2

25

10

4

6

2

36

12

4

7

2

49

14

4

8

2

64

16

4

9

2

81

18

4

10

2

100

20

4

11

3

121

33

9

12

3

144

36

9

13

3

169

39

9

14

3

196

42

9

15

3

225

45

9

16

4

256

64

16

17

4

289

68

16

18

4

324

72

16

19

4

361

76

16

20

4

400

80

16

21

4

441

84

16

22

4

484

88

16

23

4

529

92

16

24

4

576

96

16

25

5

625

125

25

26

5

676

130

25

27

5

729

135

25

28

5

784

140

25

29

5

841

145

25

30

5

900

150

25

сумма

465

101

9455

1850

379

среднее

15,50

3,37

315,17

61,67

12,63

Тогда искомые коэффициенты линейной регрессии:

.

.

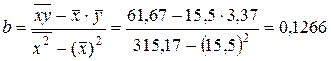Задание 2. Рассчитайте, чему равна сумма квадратов, объясненная моделью ESS, если полная сумма квадратов TSS = 0,20470, а остаточная сумма квадратов RSS = 0,161231?

Решение:

Поскольку имеет место формула TSS - RSS = ESS, то имеем

ESS = 0,2047 – 0,161231 = 0,043469.

Задание 3.  Для задания 1 рассчитайте коэффициент корреляции.

Решение:

Коэффициент корреляции рассчитывается по формуле .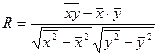

Используя вспомогательную таблицу из решения задачи 1, выполним подстановку в формулу:

.

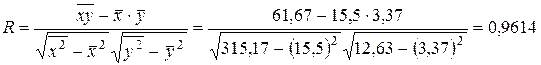Задание 4. Мы получили оценку изменения зависимой переменной (предположим расходов) от независимых (дохода DPI и цен Р) в виде:

lgT = 1.374 + 1.143 ∙ lgDPI – 0.829 ∙ lgP,

ESS = 0.097577, RSS = 0.02567,  R2 = 0.9744.

Как могут быть проинтерпретированы коэффициенты при независимых переменных?

Решение:

Коэффициент при переменной DPI показывает, на сколько увеличится зависимая переменная при увеличении логарифма DPI на единицу.

Коэффициент при переменной Р показывает, на сколько уменьшится зависимая переменная при увеличении логарифма Р на единицу.

Задание 5.  Гауссовское распределение симметрично относительно нуля, и это предполагает, что положительные ошибки столь же вероятны, как и отрицательные; при этом малые ошибки встречаются чаще, чем большие. Если случайная ошибка имеет гауссовское распределение с параметром σ, то с вероятностью 0,95 ее значение будет заключено в пределах от –1,96σ до +1,9σ. В каких интервалах будет располагаться случайная ошибка при том же значении вероятности, если σ = 0,5, σ = 1, σ = 2?

Решение:

Если σ = 0,5, то 1,96 ∙ 0,5 = 0,98, и интервал от –0,98 до +0,98.

Если σ = 1, то интервал от –1,96 до +1,96.

Если σ = 2, то 1,96 ∙ 2 = 3,92, и интервал от –3,92 до +3,92.

Задание 6. Когда и на основании чего можно говорить (утверждать) о предпочтительности одностороннего критерия по сравнению с двухсторонним при использовании в качестве альтернативной гипотезы?

Решение:

Односторонний критерий следует предпочитать в случае простой нулевой гипотезы, т.е. гипотезы вида , или  в отличие от сложной гипотезы вида . Односторонний критерий предпочтительней из-за того, что при проверке сложной гипотезы вида  необходимо проверять две гипотезы:  и . Кроме того, при применении одностороннего критерия уровень значимости в два раза выше, чем при применении двустороннего критерия.

Задание 7. Для данных о размерах совокупного располагаемого дохода и совокупных расходах на личное потребление в США в период с 1970 до 1979 год (в млрд. долл. в ценах 1972 года), оценочная модель линейной связи имеет вид  С = – 66,595 + 0,978 ∙ DPI.

Представим себе, что мы находимся в 1979 году и ожидаем увеличения в 1980 году совокупного располагаемого дохода (в тех же ценах) до DPI* = 1030 млрд. долларов. Тогда прогнозируемый доход по подобранной модели объема совокупных расходов на личное потребление в 1980 году равен

С1980 = – 66,595 + 0,978 ∙ 1030 = 940,75,

так что если выбрать уровень доверия 0,95, то

.

Чему будет равен доверительный интервал для соответствующего DPI* = 1030 значения С1980?

Решение:

Доверительный интервал . Поскольку значение среднеквадратичного отклонения не задано, пусть , тогда .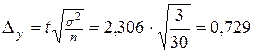

Отсюда доверительный интервал  (940,75–0,729; 940,75+0,729).

Задание 8. Рассмотрим три варианта прогноза потребления (у) электроприборов от доходов (х). Мы имеем:

·         наблюдающееся значения у1, у2, …, у20;

·         значения уi = –154,700 + 2,300хi, полученные по модели, построенной без учета автокоррелированности ошибок;

·         значения уi = –244,262 + 2,795хi, полученные по модели, параметры которой скорректированы с учетом автокоррелированности ошибок;

·         значения  уi = –244,262+2,795хi +0,874 (уi-1 + 244,262 – 2,795хi-1­).

Какому варианту модели для прогноза следует отдать предпочтение, если средние квадраты расхождение 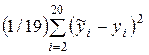 при использовании  указанных трех методов вычисления значений . Эти средние квадраты равны соответственно  MSE1 = 14.583, MSE2 = 37.025, MSE3 = 4.533?

Решение:

Следует предпочесть третью модель, т.к. метод наименьших квадратов, с помощью которого получались все три эти модели, предполагает минимальные средние квадраты, минимальный из которых соответствует третьей модели.

Задание 9. Администрация страховой компании приняла решение о введении нового вида услуг – страхование на случай пожара. С целью определения тарифов по выборке из 10 случаев пожаров анализируется зависимость стоимости ущерба, нанесенного пожаромот расстояния до ближайшей пожарной станции:

№ п/п

1

2

3

4

5

6

7

8

9

10

Ущерб

26,2

17,8

31,3

23,1

27,5

36,0

14,1

22,3

19,6

31,3

расстояние

3,4

1,8

4,6

2,3

3,1

5,5

0,7

3,0

2,6

4,3

9.1. Построить диаграмму рассеяния результирующей величины и независимой переменной.

9.2. Определить параметры а и  b уравнения линейной регрессии.

9.3. Рассчитать линейный коэффициент корреляции.

9.4. Проверить статистическую гипотезу значимости коэффициента регрессии «b» c помощью t-критерия Стьюдента.

9.5. Оценить статистическую значимость построенной модели регрессии в целом  с помощью F-критерия Фишера.

Решение:

Составим вспомогательную таблицу:

№ п/п

1

2

3

4

5

6

7

8

9

10

сумма

среднее

Х

26,2

17,8

31,3

23,1

27,5

36

14,1

22,3

19,6

31,3

249,2

24,92

У

3,4

1,8

4,6

2,3

3,1

5,5

0,7

3

2,6

4,3

31,3

3,13

ХХ

686,44

316,84

979,69

533,61

756,25

1296

198,81

497,29

384,16

979,69

6628,78

662,878

УУ

11,56

3,24

21,16

5,29

9,61

30,25

0,49

9

6,76

18,49

115,85

11,585

ХУ

89,08

32,04

143,98

53,13

85,25

198

9,87

66,9

50,96

134,59

863,8

86,38

9.1. Построить диаграмму рассеяния результирующей величины и независимой переменной.

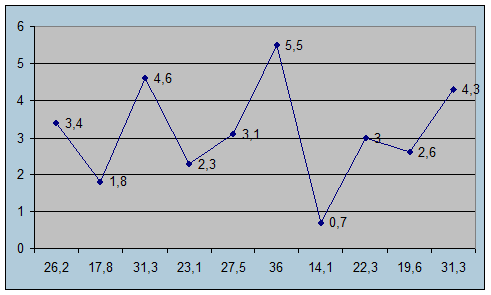
На основании поля корреляции можно сделать вывод , что между факторным (Х) и результативным (Y) признаками существует прямая зависимость.

9.2. Определить параметры а и  b уравнения линейной регрессии.

.

.

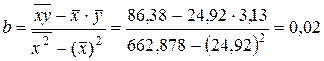9.3. Рассчитать линейный коэффициент корреляции.

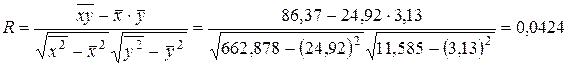
9.4. Проверить статистическую гипотезу значимости коэффициента регрессии «b» c помощью t-критерия Стьюдента.

Статистическую значимость коэффициента регрессии  «b» проверяем с помощью t-критерия Стьюдента. Для этого сначала определяем остаточную сумму квадратов:

и ее среднее квадратическое отклонение:

Найдем стандартную ошибку коэффициента регрессии по формуле:

           

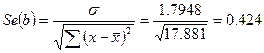
Фактическое значение t-критерия Стьюдента для коэффициента регрессии «b» рассчитывается как

Полученное фактическое значение tb сравнивается с критическим  tk , который получается по таблице Стьюдента с учетом принятого уровня значимости L=0,05 (для вероятности 0,95) и числа степеней свободы

Полученный коэффициент регрессии признается типичным, т.к.

9.5. Оценить статистическую значимость построенной модели регрессии в целом  с помощью F-критерия Фишера.

Оценка статистической значимости построенной модели регрессии  в целом производится с помощью F-критерия Фишера

      Фактическое значение критерия для уравнения определяется как

Fфакт сравнивается с критическим значением Fк, которое определяется по таблице F-критерия с учетом принятого уровня значимости L=0,05 (для вероятности 0,95) и числа степеней свободы:

Следовательно, при Fфакт>Fк уравнении регрессии в целом признается существенным.

По исходным данным полагают, что расстояние до ближайшей пожарной станции уменьшится на 5% от своего среднего уровня

Следовательно, значения факторного признака для точечного прогноза:

а точечный прогноз :

Строим доверительный интервал прогноза ущерба с вероятностью 0,95 (L=0,05) по формуле

Табличное значение t-критерия Стьюдента для уровня значимости L=0,05 и числа степеней свободы п-2=10-2=8,

Стандартная ошибка точечного прогноза рассчитываемая по формуле

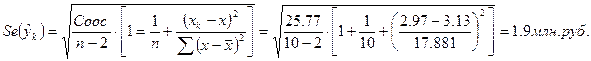Отсюда доверительный интервал составляет:

           

Из полученных результатов видно, что интервал от 19,8 до 28,6 млн. руб. ожидаемой величины ущерба довольно широкий.

Значительная неопределенность прогноза линии регрессии, это видно из формулы связана прежде всего с малым объемом выборки (n=10), а также тем, что по мере удаления x(k) от ширина доверительного интервала увеличивается.

Задание 10. Имеются следующие данные о ценах и дивидендах по обыкновенным акциям, также о доходности компании

№

Цена компании

Доходность

Уровень дивидендов

1.       

25

15,2

2,6

2.       

20

13,9

2,1

3.       

15

15,8

15,1

4.       

34

12,8

3,1

5.       

20

6,9

2,5

6.       

33

14,6

3,1

7.       

28

15,4

2,9

8.       

30

17,3

2,8

9.       

23

13,7

2,4

10.   

24

12,7

2,4

11.   

25

15,3

2,6

12.   

26

15,2

2,8

13.   

26

12

2,7

14.   

20

15,3

1,9

15.   

20

13,7

1,9

16.   

13

13,3

1,6

17.   

21

15,1

2,4

18.   

31

15

3

19.   

26

11,2

3,1

20.   

11

12,1

2

1.         построить линейное уравнение множественной регрессии и пояснить экономический смысл его параметров;

2.         определить стандартизованные коэффициенты регрессии;

3.         рассчитать частные коэффициенты эластичности;

4.         сделать вывод о силе связи результата с каждым из факторов;

5.         определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции.

Решение:

1. построить линейное уравнение множественной регрессии и пояснить экономический смысл его параметров

Составим расчетную таблицу

№

Y

X1

X2

X2*X2

X1*X1

y*X1

y*x2

X1*X2

1

25

15,2

2,6

6,76

231,04

380

65

39,52

2

20

13,9

2,1

4,41

193,21

278

42

29,19

3

15

15,8

1,5

2,25

249,64

237

22,5

23,7

4

34

12,8

3,1

9,61

163,84

435,2

105,4

39,68

5

20

6,9

2,5

6,25

47,61

138

50

17,25

6

33

14,6

3,1

9,61

213,16

481,8

102,3

45,26

7

28

15,4

2,9

8,41

237,16

431,2

81,2

44,66

8

30

17,3

2,8

7,84

299,29

519

84

48,44

9

23

13,7

2,4

5,76

187,69

315,1

55,2

32,88

10

24

12,7

2,4

5,76

161,29

304,8

57,6

30,48

11

25

15,3

2,6

6,76

234,09

382,5

65

39,78

12

26

15,2

2,8

7,84

231,04

395,2

72,8

42,56

13

26

12

2,7

7,29

144

312

70,2

32,4

14

20

15,3

1,9

3,61

234,09

306

38

29,07

15

20

13,7

1,9

3,61

187,69

274

38

26,03

16

13

13,3

1,6

2,56

176,89

172,9

20,8

21,28

17

21

15,1

2,4

5,76

228,01

317,1

50,4

36,24

18

31

15

3

9

225

465

93

45

19

26

11,2

3,1

9,61

125,44

291,2

80,6

34,72

20

11

12,1

2

4

146,41

133,1

22

24,2

Итого

471

276,5

49,4

126,7

3916,59

6569,1

1216

682,34

Определяем

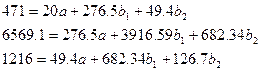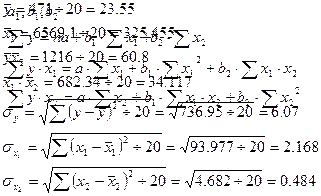По Данным таблицы составим систему нормальных уравнений с тремя неизвестными:

Разделим каждое уравнение на коэффициент при a.

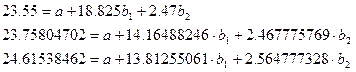Вычтем первое уравнение из второго и третьего

Разделим каждое уравнение на коэффициент при 

 

 

Сложим оба уравнения и найдем

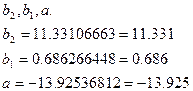
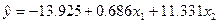Таким образом, уравнение множественной регрессии имеет вид

Экономический смысл коэффициентов        и       в  том, что это показатели силы связи, характеризующие изменение цены акции при изменении какого-либо факторного признака на единицу своего измерения при фиксированном влиянии другого фактора. Так, при изменении доходности капитала на один процентный пункт, цена акции измениться в том же направлении на 0,686 долларов; при изменении уровня дивидендов на один процентный пункт цена акции изменится в том же направлении на 11,331 доллара.

2. Рассчитать частные коэффициенты эластичности.

            Будем рассчитывать частные коэффициенты эластичности для среднего значения фактора и результата:

Э- эластичность цены акции по доходности капитала

Э- эластичность цены акции по уровню дивидендов

3. 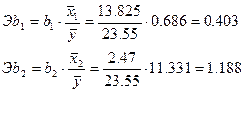Определить стандартизованные коэффициенты регрессии

            формулы определения:

где j- порядковый номер фактора

- среднее квадратическое отклонение j-го фактора (вычислено раньше)

=2,168  = ,0484

- среднее квадратическое отклонение результативного признака

=6,07

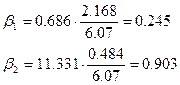4. сделать вывод о силе связи результата с каждым из факторов.

            Коэффициенты эластичности факторов  говорят о том, что при отклонении величины соответствующего фактора от его средней величины на 1% (% как относительная величина) и при отвлечении от сопутствующего отклонения другого фактора входящего в уравнение множественной регрессии, цена акции  отклонится от своего среднего значения на 0,403% при действии фактора  (доходность капитала) и на 1,188% при действии фактора (уровень дивидендов).

            Таким образом сила влияния фактора  на результат (цену акции) больше, чем фактора , а сами факторы действуют в одном и том же положительном направлениии.

            Количественно фактор  приблизительно в три раза сильнее влияет на результат чем фактор . ()

            Анализ уравнения регрессии по стандартизованным коэффициентам  показывает, что второй фактор влияет сильнее на результат, чем фактор  (), т.е. при учете вариации факторов их влияние более точно.

5. Определить парные и частные коэффициенты корреляции, а также  множественный коэффициент корреляции.

Парные коэффициенты корреляции определяются по формулам:

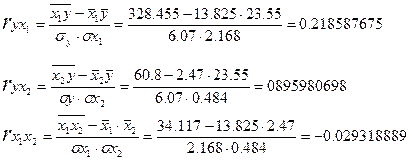
Частные коэффициенты корреляции определяются по ф-ле:

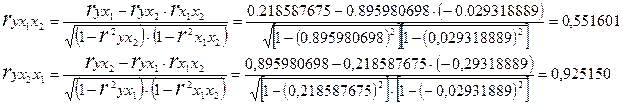            Множественный коэффициент корреляции  определяется по формуле:

Матрица парных коэффициентов корреляции

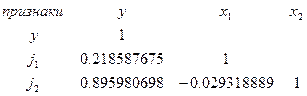
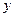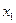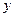Из таблицы видно, что в соответствии со шкалой Чеддока связь между  и  можно оценить как слабую, между и 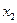- как высокую, между  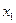и 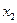 связь практически отсутствует.

            Таким образом, по построенной модели можно сделать вывод об отсутствии в ней мультиколлениарности факторов.

            Частные коэффициенты корреляции рассчитывались как оценки вклада во множественной коэффициент корреляции каждого из факторов ( и ). Они характеризуют связи между результативными признаками (ценой акции) и соответствующим фактором x при

Причина различий между значениями частных и парных коэффициентов корреляции состоит в том, что частный коэффициент отражает долю вариации результативного прихнака (цены акции), дополнительно объясняемой при включении фактора  (или ) после другого фактора  (или ) в уравнение регрессии, не объяснимой ранее включенным фактором (или ).