ВСЕРОССИЙСКИЙ
ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА
СТАТИСТИКИ
О
Т Ч Е Т
о результатах выполнения
компьютерной лабораторной работы №1
«Автоматизированный априорный анализ
статистической совокупности
в среде MS Excel»
Вариант № 6
Выполнил:
ст. III курса гр.________
Ф.И.О.
Проверил: преподаватель
Должность
Ф.И.О.
Пенза, 2006
г.
Постановка
задачи
При
проведении статистического наблюдения за деятельностью предприятий корпорации
получены выборочные данные по 32-м предприятиям, выпускающим однородную
продукцию (выборка 10%-ная,
механическая), о среднегодовой стоимости основных производственных фондов
и о выпуске продукции за год.
В
проводимом статистическом исследовании обследованные предприятия выступают как
единицы выборочной совокупности, а показатели Среднегодовая стоимость основных производственных фондов и Выпуск продукции – как изучаемые
признаки единиц.
Для
проведения автоматизированного статистического анализа совокупности выборочные
данные представлены в формате электронных таблиц процессора Excel в диапазоне
ячеек B4:C35. Выборочные данные приведены в таблице 1.
|
|
A
|
B
|
C
|
|
3
|
Номер
предприятия
|
Среднегодовая
стоимость основных производственных фондов, млн.руб.
|
Выпуск
продукции, млн. руб.
|
|
4
|
1
|
422,00
|
412,00
|
|
5
|
2
|
498,00
|
452,00
|
|
6
|
3
|
514,00
|
504,00
|
|
7
|
4
|
542,00
|
560,00
|
|
8
|
5
|
350,00
|
280,00
|
|
9
|
6
|
570,00
|
480,00
|
|
10
|
7
|
586,00
|
648,00
|
|
11
|
8
|
438,00
|
440,00
|
|
12
|
9
|
538,00
|
516,00
|
|
13
|
10
|
622,00
|
644,00
|
|
14
|
11
|
682,00
|
680,00
|
|
15
|
12
|
230,00
|
600,00
|
|
16
|
13
|
518,00
|
536,00
|
|
17
|
14
|
570,00
|
584,00
|
|
18
|
15
|
654,00
|
708,00
|
|
19
|
16
|
750,00
|
760,00
|
|
20
|
17
|
558,00
|
512,00
|
|
21
|
18
|
618,00
|
608,00
|
|
22
|
19
|
490,00
|
380,00
|
|
23
|
20
|
626,00
|
520,00
|
|
24
|
21
|
698,00
|
700,00
|
|
25
|
22
|
478,00
|
396,00
|
|
26
|
23
|
378,00
|
372,00
|
|
27
|
24
|
638,00
|
596,00
|
|
28
|
25
|
570,00
|
520,00
|
|
29
|
26
|
530,00
|
492,00
|
|
30
|
27
|
410,00
|
320,00
|
|
31
|
28
|
554,00
|
500,00
|
|
32
|
29
|
642,00
|
548,00
|
|
33
|
30
|
610,00
|
520,00
|
|
34
|
31
|
750,00
|
200,00
|
|
35
|
32
|
446,00
|
464,00
|
Статистический анализ выборочной
совокупности.
Задание 1.
Выявить
наличие среди исходных данных резко выделяющихся значений признаков («выбросов»
данных) с целью исключения из выборки аномальных единиц наблюдения.
Выявление
аномальных значений признака наиболее удобно производить графическим методом.
Для визуального анализа разброса единиц совокупности в данной работе использовался точечный
график.(Рис1)
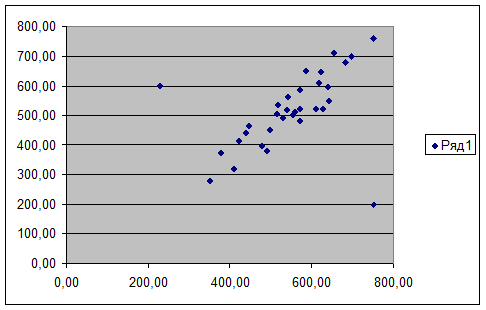
Рис 1. Аномальные значения признаков на
диаграмме рассеяния.
Любая исследуемая совокупность
может содержать единицы наблюдения, значения признаков которых резко выделяются
из основной массы значений..
В данной задаче аномальными единицами являются 2 точки с
координатами (230; 600) и (750;200) соответственно. Данные точки следует
удалить из первичных данных и поместить в таблицу 2, представленную в качестве
результативной таблицы.
Таблица 2.
|
36
|
Аномальные единицы наблюдения
|
|
37
|
|
38
|
Номер предприятия
|
Среднегодовая стоимость основных
производственных фондов, млн.руб.
|
Выпуск продукции, млн. руб.
|
|
39
|
12
|
230,00
|
600,00
|
|
40
|
31
|
750,00
|
200,00
|
Задание 2.
Рассчитать обобщающие статистические
показатели совокупности по изучаемым признакам: среднюю арифметическую (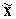 ), моду (Мо), медиану
(Ме), размах вариации (R), дисперсию(
), моду (Мо), медиану
(Ме), размах вариации (R), дисперсию(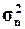 ), средние отклонения – линейное (
), средние отклонения – линейное (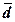 ) и квадратическое (σn),
коэффициент вариации (Vσ),
структурный коэффициент асимметрии
К.Пирсона (Asп).
) и квадратическое (σn),
коэффициент вариации (Vσ),
структурный коэффициент асимметрии
К.Пирсона (Asп).
Расчёт описательных
параметров выборочной и генеральной совокупности осуществляется с
использованием инструмента Описательная статистика. Рассчитанные таким образом
параметры отражены в результативной таблице 3.
Таблица 3
|
44
|
Описательные статистики
|
|
45
|
По столбцу "Среднегодовая
стоимость основных производственных фондов, млн.руб."
|
По столбцу "Выпуск
продукции, млн.руб"
|
|
46
|
Столбец1
|
|
Столбец2
|
|
|
47
|
|
|
|
|
|
48
|
Среднее
|
550
|
Среднее
|
521,7333333
|
|
49
|
Стандартная
ошибка
|
17,66404231
|
Стандартная
ошибка
|
21,07168571
|
|
50
|
Медиана
|
556
|
Медиана
|
518
|
|
51
|
Мода
|
570
|
Мода
|
520
|
|
52
|
Стандартное
отклонение
|
96,74994431
|
Стандартное
отклонение
|
115,4143759
|
|
53
|
Дисперсия
выборки
|
9360,551724
|
Дисперсия
выборки
|
13320,47816
|
|
54
|
Эксцесс
|
-0,344943844
|
Эксцесс
|
-0,205332365
|
|
55
|
Асимметричность
|
-0,152503649
|
Асимметричность
|
0,042954448
|
|
56
|
Интервал
|
400
|
Интервал
|
480
|
|
57
|
Минимум
|
350
|
Минимум
|
280
|
|
58
|
Максимум
|
750
|
Максимум
|
760
|
|
59
|
Сумма
|
16500
|
Сумма
|
15652
|
|
60
|
Счет
|
30
|
Счет
|
30
|
|
61
|
Уровень
надежности(95,4%)
|
36,82620681
|
Уровень
надежности(95,4%)
|
43,93050255
|
Расчёт описательных
параметров выборочной совокупности осуществляется при помощи инструмента Мастер
функций. На основе вычисленных параметров формируется таблица 5.
Таблица 5
|
81
|
Выборочные
показатели вариации и асимметрии
|
|
82
|
По столбцу "Среднегодовая
стоимость основных производственных фондов, млн.руб."
|
По столбцу "Выпуск
продукции, млн.руб"
|
|
|
83
|
Стандартное
отклонение
|
95,12377901
|
Стандартное
отклонение
|
113,4745003
|
|
84
|
Дисперсия
|
9048,533333
|
Дисперсия
|
12876,46222
|
|
85
|
Среднее
линейное отклонение
|
76,53333333
|
Среднее
линейное отклонение
|
87,41333333
|
|
86
|
Коэффициент
вариации, %
|
17,29523255
|
Коэффициент
вариации, %
|
21,74952089
|
|
87
|
Коэффициент
асимметрии
|
-0,21025237
|
Коэффициент
асимметрии
|
0,015275091
|
На основе таблиц 3 и 5 можно сформировать
таблицу 8 «Описательные статистики
выборочной совокупности».
Таблица 8. «Описательные
статистики выборочной совокупности»
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Столбец1
|
|
Столбец2
|
382,9764387
|
|
|
|
|
|
|
Среднее
|
550
|
Среднее
|
521,7333
|
|
Медиана
|
556
|
Медиана
|
518
|
|
Мода
|
570
|
Мода
|
520
|
|
Интервал
|
400
|
Интервал
|
480
|
|
Стандартное отклонение
|
95,12377901
|
Стандартное отклонение
|
113,4745003
|
|
Дисперсия
|
9048,533333
|
Дисперсия
|
12876,46222
|
|
Среднее линейное отклонение
|
76,53333333
|
Среднее линейное отклонение
|
87,41333333
|
|
Коэффициент вариации, %
|
17,29523255
|
Коэффициент вариации, %
|
21,74952089
|
|
Коэффициент асимметрии
|
-0,21025237
|
Коэффициент асимметрии
|
0,015275091
|
Задание 3.
На основе рассчитанных показателей
в предположении, что распределения единиц по обоим признакам близки к
нормальному, оценить:
а) степень колеблемости значений признаков в
совокупности;
б) степень однородности совокупности по изучаемым
признакам;
в) устойчивость индивидуальных значений признаков;
г) количество попаданий
индивидуальных значений признаков в диапазоны (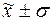 ), (
), (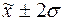 ), (
), (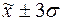 ).
).
а) Степень колеблемости признака определяется по значению коэффициента
вариации Vs., который вычисляется по формуле 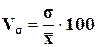 % и выражается в процентах.
% и выражается в процентах.
Для первого признака
коэффициент вариации равен 17,29523255.
Значит для первого признака колеблемость незначительная.
Для второго признака Vs=21,74952089. В данном случае так как 0%<Vs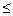 40%, колеблемость
так же будет незначительной.
40%, колеблемость
так же будет незначительной.
б) Для нормальных и близких к нормальному
распределений показатель Vs служит индикатором однородности совокупности: принято
считать, что при выполнимости неравенства
Vs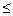 33%
33%
совокупность
является количественно однородной по данному признаку.
В данной задаче для первого признака и для
второго признаков коэффициент вариации меньше 33% значит совокупность будет
являться количественно однородной.
в) Сопоставление средних
отклонений - квадратического s и линейного  позволяют сделать вывод об
устойчивости индивидуальных значений признака, то есть об отсутствии среди
них “аномальных” вариантов значений.
позволяют сделать вывод об
устойчивости индивидуальных значений признака, то есть об отсутствии среди
них “аномальных” вариантов значений.
В
условиях симметричного и нормального, а также близких к ним распределений между
показателями s и  имеют место равенства
имеют место равенства
s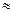 1,25
1,25 ,
, 
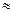 0,8s,
0,8s,
Отношение показателей
 и s может служить показателем устойчивости данных: если
и s может служить показателем устойчивости данных: если
 >0,8,
>0,8,
то значения признака
неустойчивы, в них имеются «аномальные» выбросы.
Для первого признака данное отношение
составляет:
 =
=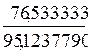 =0,8045657
=0,8045657
Для второго признака это отношение составляет:
 =
=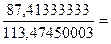 0,77
0,77
Так как у второго признака данное
отношение меньше 0.8, то, следовательно исследуемые значения признака устойчивы
и в них нет «аномальных выбросов» . У второго же признака данное отношение
больше 0,8, следовательно исследуемые значения признака неустойчивы, и в них
имеются «аномальные» выбросы.
г)
Распределение значений
признака по диапазонам
рассеяния признака
относительно 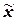
|
|
Границы диапазонов
|
Количество
значений xi,
находящихся в диапазоне
|
|
|
Первый
признак
|
Второй
признак
|
Первый
признак
|
Второй
признак
|
|
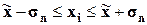
|
(454,87;
645,12)
|
(408,26;
635,2)
|
20
|
19
|
|
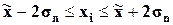
|
(359,75;
740,25)
|
(294,78;
748,68)
|
28
|
28
|
|
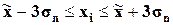
|
(264,63;
835,37)
|
(181,31;
862,16)
|
30
|
30
|
Таблица 9.
На основе данных таблицы
определим процентное соотношение рассеяний значения признака по трём диапазонам
и сопоставим его с ожидаемым по правилу « трёх сигм» (68,3%; 95,4%;99,7%). Для
первого признака процентное соотношение составляет: 66,67%; 93,33%;100%. А для
второго - 63,33%;93,33%;100%.
Задание 4.
Дать сравнительную характеристику
распределений единиц совокупности по двум изучаемым признакам на основе
анализа:
а) вариации признаков;
б) количественной однородности единиц;
в) надежности (типичности) средних значений признаков;
г) симметричности распределений
в центральной части ряда
а)
мода Мо - наиболее часто встречающийся вариант значений признака или тот
вариант, который соответствует максимальной ординате эмпирической кривой
распределения. В данном случае для первого признака она равна 570, а для второго - 520.
медиана Ме -
серединное значение ранжированного ряда вариантов значений признака. Для
первого признака в данной задаче медиана равна 556, а для второго 518.
К
показателям размера вариации относятся:
1) размах вариации R= xmax - xmin,
устанавливающий предельное значение амплитуды колебаний признака. Для первого
признака данный показатель равен 400, а для второго 428.
2) среднее линейное
отклонение 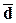 , которое вычисляется как среднее арифметическое из
абсолютных отклонений |xi -
, которое вычисляется как среднее арифметическое из
абсолютных отклонений |xi -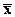 |,для первого признака равно 76,53333333,
а для второго 87,41333333
.
|,для первого признака равно 76,53333333,
а для второго 87,41333333
.
3) дисперсия s2, рассчитываемая как среднее арифметическое из квадратов отклонений (xi -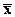 ).Дисперсия для первого признака равна 9048,533333,
а для второго
-12876,46222.
).Дисперсия для первого признака равна 9048,533333,
а для второго
-12876,46222.
4) Среднее квадратическое
отклонение s,
показывающее, на сколько в среднем отклоняются конкретные варианты от их
среднего значения. Этот показатель равен 95,12377901 и 113,4745003для первого и второго признаков
соответственно.
б) Однородность совокупности устанавливается по коэффициенту
вариации. Для данной задачи совокупность является количественно однородной, так
как коэффициент вариации для обоих признаков меньше 33%.
в) Для оценки надёжности
(типичности) средних значений признаков 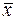 можно воспользоваться
значением коэффициента вариации, Vs.. Значение коэффициента вариации не превышают 40 %, поэтому индивидуальные
значения признака xi мало
отличаются друг от друга, единицы наблюдения количественно однородны и,
следовательно, средняя арифметическая величина
можно воспользоваться
значением коэффициента вариации, Vs.. Значение коэффициента вариации не превышают 40 %, поэтому индивидуальные
значения признака xi мало
отличаются друг от друга, единицы наблюдения количественно однородны и,
следовательно, средняя арифметическая величина 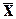 является надежной
характеристикой данной совокупности.
является надежной
характеристикой данной совокупности.
г) Для анализа формы распределения на её близость
к нормальной форме используют показатель асимметрии - коэффициент асимметрии Пирсона Asп,, который оценивает асимметричность распределения в
центральном диапазоне. Коэффициенты
асимметрии для первого и второго признака равны -0,21025237 и 0,015275091соответственно.
В симметричном
распределении характеристики центра распределения совпадают 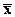 =Mo=Me. В нашем случае этого не наблюдается ни для одного признака, поэтому
вершина кривой находится не в середине, а сдвинута либо влево, либо
вправо. Для оценки асимметричности распределения служит коэффициент Пирсона.
Для первого признака наблюдается левостороння асимметрия, так как As<0 , а для второго признака правосторонняя. В
нашем примере для обоих признаков асимметрия незначительна, так как в обоих случаях |As|<0,25.
=Mo=Me. В нашем случае этого не наблюдается ни для одного признака, поэтому
вершина кривой находится не в середине, а сдвинута либо влево, либо
вправо. Для оценки асимметричности распределения служит коэффициент Пирсона.
Для первого признака наблюдается левостороння асимметрия, так как As<0 , а для второго признака правосторонняя. В
нашем примере для обоих признаков асимметрия незначительна, так как в обоих случаях |As|<0,25.
Задание
5.
Построить интервальный вариационный ряд и
гистограмму распределения единиц совокупности по признаку Среднегодовая стоимость основных
производственных фондов и установить характер (тип) этого распределения.
Рассчитать моду Мо полученного
интервального ряда и сравнить ее с показателем Мо несгруппированного ряда данных.
Выполнение задания
осуществляется в три этапа:
1.
Построение
промежуточной таблицы.
2.
Генерация
выходной таблицы и графиков.
3.
Приведение
выходной таблицы и диаграммы к виду, принятому в статистике.
Гистограмма и выходная таблица приведены ниже.
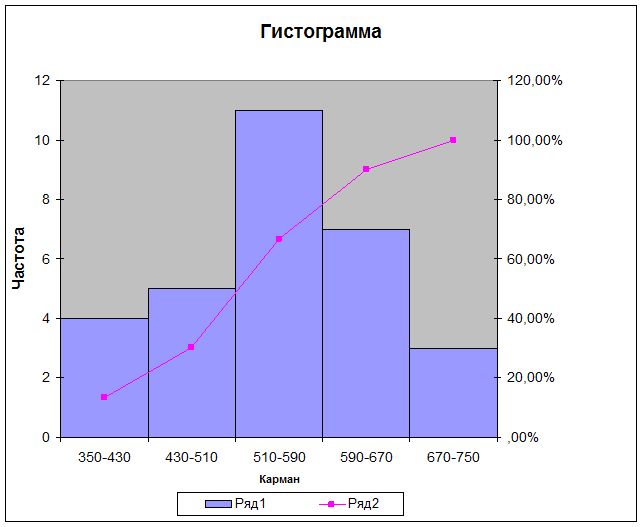
|
Группа предприятий по стоимости
основных фондов
|
Число предприятий в группе
|
Накопленная частость группы.%
|
|
350-430
|
4
|
13,33%
|
|
430-510
|
5
|
30,00%
|
|
510-590
|
11
|
66,67%
|
|
590-670
|
7
|
90,00%
|
|
670-750
|
3
|
100,00%
|
|
Итого
|
30
|
|
Для полученного интервального ряда значение моды
рассчитывается по формуле:
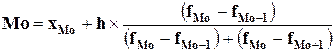 ,
,
где: хМо – нижняя граница модального интервала;
h – величина модального интервала;
fMo – частота модального интервала;
fMo-1 – частота интервала, предшествующего модальному;
fMo+1 – частота интервала, следующего за модальным.
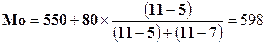 (млрд. руб.)
(млрд. руб.)
Мода интервального ряда,
равная 598 млрд. рублей и не
сгруппированного - 570 млрд. руб. расходятся, так как описательные статистики, рассчитанные по
несгрупированным данным, реализуют точные функциональные зависимости значений
показателей от исходных данных, в отличие от приближённых статистических
оценок, выводимых с заданным уровнем надёжности.
Статистический
анализ генеральной совокупности.
Задание 1.
Рассчитать генеральную дисперсию  , генеральное среднее
квадратическое отклонение
, генеральное среднее
квадратическое отклонение 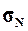 и ожидаемый размах
вариации признаков RN. Сопоставить значения этих показателей для
генеральной и выборочной дисперсий.
и ожидаемый размах
вариации признаков RN. Сопоставить значения этих показателей для
генеральной и выборочной дисперсий.
Генеральные показатели рассчитываются с помощью инструмента
Описательная статистика и их значения приведены в таблице 3. Сформируем для них отдельную таблицу № 10 .
Таблица 10.
|
По столбцу "Среднегодовая стоимость основных
производственных фондов, млн.руб."
|
По столбцу "Выпуск продукции, млн.руб"
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
|
Стандартное отклонение
|
96,74994431
|
Стандартное отклонение
|
115,4143759
|
|
Дисперсия выборки
|
9360,551724
|
Дисперсия выборки
|
13320,47816
|
|
Эксцесс
|
-0,344943844
|
Эксцесс
|
-0,205332365
|
|
Асимметричность
|
-0,152503649
|
Асимметричность
|
0,042954448
|
Величина дисперсии генеральной
совокупности σ2N может быть
оценена по выборочной дисперсии σ2n,
Установить степень расхождения между данными признаками можно по формуле (1).
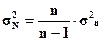 (1)
(1)
Вычислим σ2N для обоих признаков:
1)
σ2N
=.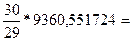 9683,3293696;
9683,3293696;
2)
σ2N
=.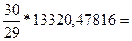 13779,8049931;
13779,8049931;
Если
сравнить дисперсии генеральной совокупности обоих признаков(σ2N ) с дисперсиями выборки (
σ2n. ), то можно считать что обе дисперсии приближенно равны, а
значит степень расхождения признаков не значительна.
В условиях близости
распределения единиц генеральной совокупности к нормальному соотношение R=6s используется для прогнозной оценки размаха вариации
признака в генеральной совокупности.
Для первого признака RN= 6*96,74994431=580,49966586
Rn=6*95,12377901=681,9663024
Для второго признака RN=6*115,4143759=692,4862554
Rn=6*113,4745003=745,5464022
Если сравнивать размах
вариации для генеральной совокупности, то можно увидеть, что он немного меньше
аналогичного признака для выборочной.
Задание 2.
Для изучаемых признаков рассчитать:
а) среднюю ошибку выборки;
б) предельные ошибки
выборки для уровней надежности
P=0,683, P=0,954,
P=0,997 и границы, в которых будут
находиться средние
значения признака генеральной
совокупности
при заданных уровнях надежности.
а) Средняя ошибка выборки 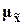 выражает среднее квадратическое
отклонение s выборочной средней
выражает среднее квадратическое
отклонение s выборочной средней 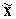 от математического
ожидания M[
от математического
ожидания M[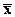 ] генеральной средней
] генеральной средней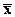 . Средняя ошибка выборки рассчитана для обоих признаков и
равна для первого признака соответственно 17,66404231, а для второго-21,07168571.
. Средняя ошибка выборки рассчитана для обоих признаков и
равна для первого признака соответственно 17,66404231, а для второго-21,07168571.
б)Предельные ошибки выборки при уровнях надежности
68,3 и 99,7 расчитаны а таблице 4а и 4б
|
65
|
|
|
|
Таблица 4а
|
|
66
|
Предельные ошибки выборки
|
|
67
|
По столбцу "Среднегодовая
стоимость основных производственных фондов, млн.руб."
|
По столбцу "Выпуск
продукции, млн.руб"
|
|
68
|
Столбец1
|
|
Столбец2
|
|
|
69
|
|
|
|
|
|
70
|
Уровень
надежности(68,3%)
|
17,98562444
|
Уровень
надежности(68,3%)
|
21,45530558
|
|
71
|
|
|
|
|
|
72
|
|
|
|
|
|
73
|
|
|
|
Таблица
4б
|
|
74
|
Предельные ошибки выборки
|
|
75
|
По столбцу "Среднегодовая
стоимость основных производственных фондов, млн.руб."
|
По столбцу "Выпуск
продукции, млн.руб"
|
|
76
|
Столбец1
|
|
Столбец2
|
|
|
77
|
|
|
|
|
|
78
|
Уровень
надежности(99,7%)
|
57,22093133
|
Уровень
надежности(99,7%)
|
68,25965765
|
|
79
|
|
|
|
|
Придельные ошибки выборки
и ожидаемые границы для средних приведены в таблице 11.
Таблица 11.
|
Доверительная
вероятность
Р
|
Коэффициент
доверия
t
|
Предельные ошибки выборки
|
Ожидаемые границы для средних 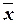
|
|
для первого
признака
|
для второго
признака
|
для первого
признака
|
для второго
признака
|
|
0,683
|
1
|
17,98562444
|
21,45530055
|
532,34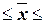
567,66
|
500,66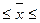
542,804
|
|
0,954
|
2
|
36,82620681
|
43,93050255
|
514,67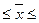
585,33
|
479,59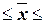
536,88
|
|
0,997
|
3
|
57,22093133
|
68,25965765
|
497,008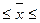 602,99 602,99
|
458,52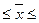
584,95
|
Задание 3.
Рассчитать
коэффициенты асимметрии As и
эксцесса Ek. На основе полученных
оценок сделать вывод о степени близости
распределения единиц генеральной совокупности к нормальному распределению
Значения коэффициентов асимметрии и эксцесса
следующие для первого и второго признаков соответственно: -0,175961071 и 0,042954448; -0,344943844 и
-0,205332365.
Для заключения
о степени близости распределения единиц
генеральной совокупности к нормальной форме следует обратиться к графику
распределения, проанализировать полученную гистограмму и выяснить, на сколько
нарушено предположение о нормальности.
Гистограмма имеет одновершинную форму, поэтому
можно предположить, что выборка является однородной по данному признаку.
As характеризует несимметричность
распределения, а Ek характеризует крутизну кривой распределения - ее
заостренность или пологость по сравнению с нормальной кривой. Для первого
признака коэффициент эксцесса Ek>0, поэтому
вершина кривой распределения располагается выше
вершины нормальной кривой. Для второго признака Ek<0,
поэтому вершина кривой распределения находится ниже вершины кривой нормального
распределения.
В данном примере наблюдается
небольшое нарушение соотношения нормального распределения 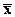 =Mo=Me As=0 Asп=0 R=6s, поэтому это
свидетельствует о наличии небольшой асимметрии. Но в целом можно сказать, что
гистограмма приблизительно симметрична и
она представляет распределение близкое к нормальному.
=Mo=Me As=0 Asп=0 R=6s, поэтому это
свидетельствует о наличии небольшой асимметрии. Но в целом можно сказать, что
гистограмма приблизительно симметрична и
она представляет распределение близкое к нормальному.
Таким образом, распределение единиц
выборочной совокупности близко к нормальному,
выборка является репрезентативной и при этом коэффициенты AsN, EkN
указывают на небольшую или умеренную величину асимметрии и эксцесса
соответственно, значит есть основание полагать, что распределение единиц
генеральной совокупности по изучаемому признаку будет близко к нормальному.