Контрольная работа № 3.

Задание 1.

Определить, является ли справедливой приведённая формула алгебры высказываний, не прибегая к составлению таблицы истинности, а используя только свойства соответствующих операций:

 где А, В, С, D, Е – простые высказывания.

Решение:

По правилу Моргана получаем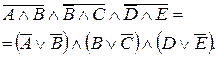

Нет полного совпадения с правой частью приведённой формулы. Значит, она не является справедливой.

Задание 2.

Для указанной функции трёх переменных: f (х₁, х₂, х₃) – принимает единичные значения на наборах № 0, 1, 3, 6, 7.

- составить таблицу истинности;

- определить, к каким классам булевых функций она относится;

- записать совершенные ДНФ и КНФ;

- найти минимальную ДНФ;

- для полученной минимальной ДНФ построить логическую схему в базисах:

а)  (дизъюнкция, отрицание);

б)  (конъюнкция, отрицание).

Решение:

Составим таблицу истинности для функции f и двойственной функции f^* (х₁, х₂, х₃) =

№	Х1	Х2	Х3	f	f*
0	0	0	0	1	0
1	0	0	1	1	0
2	0	1	0	0	1
3	1	0	0	1	1
4	0	1	1	0	0
5	1	0	1	0	1
6	1	1	0	1	0
7	1	1	1	1	0

Функция f не сохраняет 0, сохраняет 1, не является самодвойственной, т.к.  Функция f не является монотонной, т.к. на нулевом наборе она равна 1 и равна 0 на наборах с номерами 2, 4 и 5, что противоречит определению монотонности. Проверяем свойство линейности.

а₀ + а₁х₁ + а₂х₂ + а₃х₃ = f.

Проходя по таблице истинности сверху вниз, получаем а₀ = 1,

а₀ + а₂ = 0, откуда а₂ = -1, что невозможно в определении линейности.

Способ перехода от табличного задания логической функции к СДНФ: для каждого набора значений переменных х₁, х₂, х₃, на котjром функция

f (х₁, х₂, х₃) равна 1, выписываются конъюнкции всех переменных: над переменными, которые на этом  наборе равны 0, ставятся отрицания; все такие конъюнкции соединяются знаками дизъюнкции. В результате СДНФ имеет вид:

f.

Правило получения СКНФ функции по её таблице истинности: СКНФ строится из элементарных дизъюнкций, соответствующих обратным наборам, на которых функция равна нулю. В результате СКНФ имеет вид:

Минимальную ДНФ найдём методом Блейка-Порецкого. Метод заключается в попарном склеивании всех элементарных конъюнкций СДНФ между собой, а также полученных в процессе склеивания элементарных конъюнкций меньшего числа переменных и затем – поглощение конъюнкциями меньшего числа переменных. Пронумеруем элементарные конъюнкции СДНФ и под результатом склеивания проставим номера склеиваемых конъюнкций.

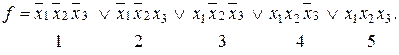
Проведём все возможные попарные склеивания:

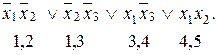
Теперь

Затем выполняем поглощения

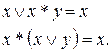
Получаем   

Этой минимальной ДНФ соответствует логическая схема в базисе

По первому закону де Моргана

по второму закону

а) Поэтому в базисе  получается логическая схема:

;

б) В базисе  будет .

Задание 3.

Является ли полной система булевых функций, состоящая из импликации и отрицания? Доказать полноту (или неполноту) приведённой системы булевых функций, состоящей из импликации и отрицания.

Решение:

Полнота системы булевых функций  доказана в теореме 11.2, учебного пособия . В основе доказательства лежит

Теорема 10.5. Всякая булева функция  может быть представлена в виде суперпозиции конъюнкции, дизъюнкции и отрицания, причём знак отрицания стоит только непосредственно около переменной и не стоит ни перед одной из внутренних скобок.

Конъюнкцию можно выразить через дизъюнкцию и отрицание. Так утверждает теорема 9.5. а)  : .

Остаётся дизъюнкцию выразить через импликацию: .

Так утверждает теорема 9.5. в).

Теперь остаётся напомнить основное определение 11.1. Система булевых функций называется полной, если всякая булева функция является суперпозицией функций из этой системы.

Литература

1. Игошин В.И. Математическая логика и теория алгоритмов: Учеб. пособие для студ. высш. учеб. заведений. – М.: Издательский центр «Академия», 2004.

2. Москинова Г.И. Дискретная математика. Математика для менеджера в примерах и упражнениях: Учебное пособие. – М.: Логос, 2004.

Контрольная работа № 4.

Задание 1.

Привести три самостоятельных примера применения оператора подстановки к простейшим числовым функциям.

Решение:

К простейшим функциям относятся:

 (функция следования)

О (х) = 0 (нуль-функция)

 (функция-проектор).

Оператор подстановки в учебном пособии  называется оператором суперпозиции. О нём говорят, когда из m – местной функции f и n – местных функций q₁,q₂, …, q_m получается n - местная функция.

Пример 1.

В качестве функций q₁, q₂, …,q_n возьмём

В качестве функции f (х₁,…х_n) возьмём функцию

Тогда

Пример 2.

В качестве функций q₁, q₂,…,q_nвозьмём S (х).

В качестве функции f (х₁,…, х_n) возьмём снова функцию

Тогда

Рассмотрим ещё n- местную нуль-функцию Оⁿ (х₁,…,х_n) = 0.

Пример 3.

Пусть q₁ (х₁,…,х_n) =

q₂ (х₁,…,х_n) = Oⁿ (х₁,…,х_n)

  Тогда

q₂ (x₁,…,x_n)) =

Задание 2.

Привести два самостоятельных примера применения оператора примитивной рекурсии.

Решение:

Оператор примитивной рекурсии заключается в том, что из n – местной функции  и (n + 2) – местной функции  получается (n + 1) – местная функция  такая, что:

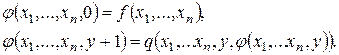
Пример1.Пусть  

Тогда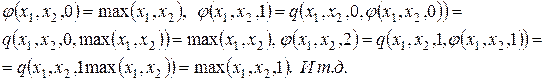

Пример 2.

Пусть

Тогда

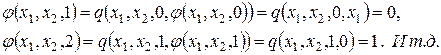
          Задание 3.

Составить программу машины Тьюринга, уменьшающей данное число на единицу. В результате работы программы происходит следующее преобразование машинных слов:

01^х q₁ 170 01^х+у-2 q₀ 100.

Решение:

Пусть П – обозрение правой ячейки, Л – обозрение левой ячейки, С – обозрение той же ячейки. Рассмотрим внешний алфавит А = и алфавит внутренних состояний Q=, где q₁ – начальное состояние, q₀ – заключительное состояние.

Программа Тьюринга выглядит следующим образом:

q₁ O → q₂ O Л;

q₂ O → q₁ 1 C;

q₁ 1 → q₁ 1 П;

q₂ 1 → q₀  О Л.

Её можно представить в виде таблицы:

А/Q	q1	q2
0	q2 О Л	q1 1 С
1	q1 1 П	q0 О Л

В подробной записи исходное машинное слово выглядит так:

Чтобы в двоичной системе из числа    вычесть единицу, машина Тьюринга должна обнаружить самую правую единицу, заменить её нулём и после этого остановиться.

          Задание 4.

Из колоды карт, содержащей 52 карты, вынули 10 карт. В скольких случаях окажется, что среди вынутых карт: а) хотя бы один туз;

б) ровно один туз.

Решение:

а) Всего существует С  способов вынуть из колоды 10 карт, при этом совсем не будет тузов в Сслучаях. Значит, ответом будет число С.

б) Если вынут ровно один туз конкретной масти, то число способов будет С. Но в колоде 4 разных туза. Значит, в 4 раза увеличится число нужных комбинаций: 4*С.