Министерство общего и профессионального образования

Российской Федерации

Южно-Уральский Государственный Университет

Кафедра АиУ.

Реферат

по математическим основам теории систем

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Выполнил: Подрезов Сергей Валерьевич

Группа: ПС-243

Преподаватель: Разнополов Олег Александрович

Челябинск, 2005

Содержание.

Линейное программирование. 3

Симплекс-метод. 6

Двойственная задача. 13

Список используемой литературы. 14

Линейное программирование.

       

Постановка задачи

Термин и линейное программирование связывается со следующей задачей. Дана система линейно независимых уравнений с неизвестными х1,….,х2 – система ограничений задач и линейного программирования:

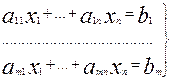,  (1)

где b_i≥0. Требуется найти неотрицательное значение переменных (х_i≥0), которые удовлетворяют управлениям (1) и обращают в минимум целевую функцию q = c₁x₁+…+c_nx_n (2), называемой линейной формой.

Матричная запись:

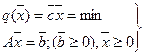  (3)

Если m<n, то система (1) имеет бесчисленное множество решений. Любое решение системы (1), где x_i≥0 будем называть допустимым решением. Среди допустимых решений нужно выбрать такое, которое обращает в минимум целевую функцию.

В ограничения (1) могут входить не равенства a_j1x₁+..+a_jnx_n≤b_j или a_j1x₁+..+a_jnx_n≥b_j  введя дополнительную переменную x_n+j так, чтобы имело место: a_j1x₁+..+a_jnx_n+x_n+j=b_j или a_j1x₁+..+a_jnx_n-x_n+j=b_j что не меняет существа задачи. Задача максимизации сводится к рассмотренной путем замены знака целевой функции .

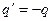Базисом называют набор m переменных таких, что определить, составленный из коэффициентов, при этих переменных не равен нулю. Эти переменных называют базисными. Если положить все свободные переменные равными нулю и решить полученную систему m уравнений с m неизвестными, то получим базисное решение. Допустимыми базисными решениями являются такие, которые дают неотрицательные значения базисных переменных.

 

Геометрическая интерпретация

g=x₂-x₁  (4)

при ограничениях

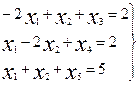.  (5)

Удобнее решить задачу максимизации q^/ = -q= x₁-x₂. (6)

Имеется m=3 базисных переменных и n-m=2 свободных. Выразим базисные переменные через свободные  .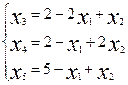

Область допустимых значений: x_i≥0, 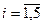. Построим прямые x₃, x₄, x₅ на плоскости x₁, x₂:

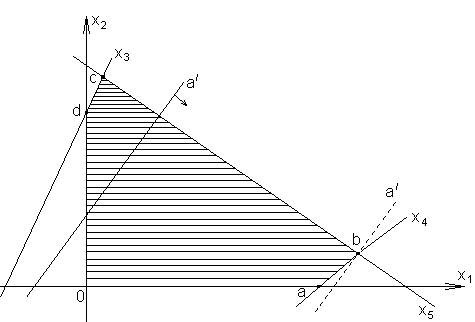
Для каждой прямой x_i переменных x_i=0. В точках пересечения 2-х прямых в нуль обращаются две переменные, что соответствует базисному решению. Вершины многоугольника допустимых решений соответствуют допустимым базисным решениям. Выражение (6) определяет прямую, причём увеличение q^/ соответствует перемещению прямой в направлении стрелки. Эта прямая должна проходить через область допустимых решений. Максимум q^/ получим в крайнем положении прямой (пунктир). Таким образом, решение, обращающее в максимум целевую функцию q^/, обязательно лежит среди допустимых базисных  решений. Т.к. их число, конечно, то можно найти все допустимые базисные решения и для каждого из них вычислить значение q^/. Окончательным решением будет, то для которого q^/ будет максимально.

Наиболее распространённый метод такого перебора решений – это симплекс – метод.

 

Алгебра симплекс – метода.

Существо метода состоит в следующем. Находим какое-нибудь базисное решение. Далее проверяем, не достигнут ли уже максимум целевой функции. Если нет, то ищем новое допустимое базисное решение, но не любое, а такое, которое увеличивает значение q^/. Затем процедуру повторяем. Для перехода к новому допустимому базисному решению одну из свободных переменных следует сделать базисной. При этом она станет отличной от нуля и будет возрастающей. Если какая либо свободная переменная входит в целевую функцию со знаком «+», т.е. при её увеличении целевая функция увеличивается, то максимум не достигнут и данную переменную следует сделать базисной (отличной от нуля).

 

Математическое описание.

Использование графического способа удобно только при решении задач ЛП с двумя переменными. При большем числе переменных необходимо применение алгебраического аппарата . В данной главе рассматривается общий метод решения задач ЛП , называемый симплекс-методом .

            Информация, которую можно получить с помощью симплекс-метода, не ограничивается лишь оптимальными значениями переменных.

          Процесс решения задачи линейного программирования носит итерационный характер: однотипные вычислительные процедуры в определенной последовательности повторяются до тех пор, пока не будет получено оптимальное решение. Процедуры , реализуемые в рамках симплекс-метода , требуют применения вычислительных машин - мощного средства решения задач линейного программирования .

           Симлекс-метод - это характерный пример итерационных вычислений, используемых при решении большинства оптимизационных задач. 

          Правая и левая части ограничений линейной модели могут быть связаны знаками <=, = и =>. Кроме того, переменные, фигурирующие в задачах ЛП, могут быть неотрицательными или не иметь ограничения в знаке. Для построения общего метода решения задач ЛП соответствующие модели должны быть представлены в некоторой форме, которую назовем стандартной формой линейных оптимизационных моделей. При стандартной форме линейной модели.

1.   Все ограничения записываются в виде равенств с неотрицательной правой частью;

2.   Значения всех переменных модели неотрицательны;

3.   Целевая функция подлежит максимизации или минимизации.

Покажем, каким образом любую линейную модель можно привести к стандартной.

Ограничения

1.   Исходное ограничение, записанное в виде неравенства типа <= ( =>), можно представить в виде равенства, прибавляя остаточную переменную к левой части ограничения (вычитая избыточную переменную из левой части).

Например, в левую часть исходного ограничения

5X1 + 100X2 <= 1000

вводится остаточная переменная S1 > 0 , в результате чего исходное неравенство обращается в равенство

5X1 + 100X2 + S1 = 1000 , S1 => 0

Если исходное ограничение определяет расход некоторого ресурса, переменную S1 следует интерпретировать как остаток, или неиспользованную часть, данного ресурса.

      Рассмотрим исходное ограничение другого типа:

X1 - 2X2 => 0

Так как левая часть этого ограничения не может быть меньше правой, для обращения исходного неравенства в равенство вычтем из его левой части избыточную переменную S2 > 0 . В результате получим

X1 - 2X2 - S2 = 0, S2 => 0

2.   Правую часть равенства всегда можно сделать неотрицательной, умножая оби части на-1 .

Например, равенство  X1 - 2X2 - S2 = 0 эквивалентно равенству - X1 + 2X2 + S2 = 0

3.   Знак неравенства изменяется на противоположный при умножении обеих частей на -1.

Например, можно вместо 2 < 4 записать - 2 > - 4 , неравенство X1 - 2X2 <= 0 заменить на - X1 + 2X2 => 0

Переменные

Любую переменную Yi , не имеющую ограничение в знаке, можно представить как разность двух неотрицательных переменных:

Yi=Yi’-Yi’’, где Yi’,Yi’’=>0.

Такую подстановку следует использовать во всех ограничениях, которые содержат исходную переменную Yi , а также в выражении для целевой функции.

Обычно находят решение задачи ЛП, в котором фигурируют переменные Yi’ и Yi’’ , а затем с помощью обратной подстановки определяют величину Yi . Важная особенность переменных Yi’ и Yi’’ состоит в том, что при любом допустимом решении только одна из этих переменных может принимать положительное значение, т.е. если Yi’>0 , то Yi’’=0, и наоборот. Это позволяет рассматривать Yi’ как остаточную переменную, а Yi’’ - как избыточную переменную, причем лишь одна из этих переменных может принимать положительное значение. Указанная закономерность широко используется в целевом программировании и фактически является предпосылкой для использования соответствующих преобразований.

Целевая функция

Целевая функция линейной оптимизационной модели, представлена в стандартной форме, может подлежать как максимизации, так и минимизации. В некоторых случаях оказывается полезным изменить исходную целевую функцию .

Максимизация некоторой функции эквивалентна минимизации той же функции, взятой с противоположным знаком, и наоборот. Например максимизация функции

Z = X1 + 25X2

эквивалентна минимизации функции

(-Z) = -X1 - 25X2

Эквивалентность означает, что при одной и той же совокупности ограничений оптимальные значения X1 , X2 , в обоих случаях будут одинаковы. Отличие заключается только в том , что при одинаковых числовых значениях целевых функций их знаки будут противоположны.

Симплекс-метод.

 

В вычислительной схеме симплекс-метода реализуется упорядоченный процесс, при котором, начиная с некоторой  исходной допустимой угловой точки (обычно начало координат), осуществляются последовательные переходы от одной допустимой экстремальной точки к другой до тех пор, пока не будет найдена точка, соответствующая оптимальному решению.

Исходной точкой алгоритма является начало координат. Решение, соответствующее этой точке, обычно называют начальным решением. От исходной точки осуществляется переход к некоторой смежной угловой точке.

Выбор каждой последующей экстремальной точки при использовании симплекс-метода определяется следующими двумя правилами.

1.   Каждая последующая угловая точка должна быть смежной с предыдущей. Этот переход осуществляется по границам (ребрам) пространства решений.

2.   Обратный переход к предшествующей экстремальной точке не может производиться.

Таким образом, отыскание  оптимального решения начинается с некоторой допустимой угловой точки, и все переходы осуществляются только к смежным точкам, причем перед новым переходом каждая из полученных точек проверяется на оптимальность.

Определим пространство решений и угловые точки алгебраически. Требуемые соотношения устанавливаются из указанного в таблице соответствия геометрических и алгебраических определений.

Геометрическое определение	Алгебраическое определение (симплекс метод)
Пространство решений	Ограничения модели стандартной формы
Угловые точки	Базисное решение задачи в стандартной форме

 

Представление пространства решений стандартной задачи линейного программирования.

Линейная модель, построенная для нашей задачи и приведенная к стандартной форме, имеет следующий вид:

Максимизировать

                              Z = X1 + 25X2 + 0S1 + 0S2

При ограничениях

5X1 + 100X2 +    S1              = 1000

- X1   +     2X2                   + S2 = 0

X1=>0, X2=>0, S1=>0, S2=>0

Каждую точку пространства решений данной задачи можно определить с помощью переменных X1 , X2 , S1 и S2 , фигурирующими в модели стандартной формы. При S1 = 0 и S2 = 0 ограничения модели эквивалентны равенствам, которые представляются соответствующими ребрами пространства решений. Увеличение переменных S1 и S2 будет соответствовать смещению допустимых точек с границ пространства решений в его внутреннюю область. Переменные X1 , X2 , S1 и S2 , ассоциированные с экстремальными точками А, В,  и С можно упорядочить, исходя из того, какое значение (нулевое или ненулевое) имеет данная переменная в экстремальной точке.

Экстремальная точка	Нулевые переменные	Ненулевые переменные
А	S2 , X2	S1 , X1
В	S1 , X2	S2 , X1
С	S1 , S2	X1 , X2

Анализируя таблицу, легко заметить две закономерности:

1. Стандартная модель содержит два уравнения и четыре неизвестных, поэтому в каждой из экстремальных точек две (= 4 - 2) переменные должны иметь нулевые значения .

2. Смежные экстремальные точки отличаются только одной переменной в каждой группе (нулевых и ненулевых переменных), Первая закономерность свидетельствует о возможности определения экстремальных точек алгебраическим способом путем приравнивания нулю такого количества переменных, которое равно разности между количеством неизвестных и числом уравнений. В этом состоит сущность свойства однозначности экстремальных точек. Каждой не экстремальной точке соответствует не более одной нулевой переменной . Так , любая точка внутренней области пространства решений вообще не имеет ни одной нулевой переменной, а любая не экстремальная точка , лежащая на границе, всегда имеет лишь одну нулевую переменную.

Свойство однозначности экстремальных точек позволяет определить их алгебраическим методом. Будем считать, что линейная модель стандартной формы содержит т уравнений и п ( т <= п ) неизвестных (правые части ограничений — неотрицательные). Тогда все допустимые экстремальные точки определяются как все однозначные неотрицательные решения системы m уравнений , в которых п — m  переменных равны нулю.

Однозначные решения такой системы уравнений, получаемые путем приравнивания к нулю ( п — т) переменных, называются базисными решениями. Если базисное решение удовлетворяет требованию неотрицательности правых частей , оно называется допустимым базисным решением. Переменные, имеющие нулевое значение, называются небазисными переменными, остальные — базисными переменными.

Из вышеизложенного следует, что при реализации симплекс метода алгебраическое определение базисных решений соответствует идентификации экстремальных точек, осуществляемой при геометрическом представлении пространства решений. Таким образом , максимальное число итераций при использовании симплекс метода равно максимальному числу базисных решений задачи ЛП, представленной в стандартной форме . Это означает , что количество итерационных процедур симплекс-метода не превышает

C^п_т= n! / [ ( n - m)!m!]

Вторая из ранее отмеченных закономерностей оказывается весьма полезной для построения вычислительных процедур симплекс-метода, при реализации которого осуществляется последовательный переход от одной экстремальной точки к другой, смежной с ней. Так как смежные экстремальные точки отличаются только одной переменной, можно определить каждую последующую (смежную) экстремальную точку путем замены одной из текущих небазисных (нулевых) переменных текущей базисной переменной. В нашем случае получено решение, соответствующее точке А , откуда следует осуществить переход в точку В. Для этого нужно увеличивать небазисную переменную X₂ от исходного нулевого значения до значения, соответствующего точке В. В точке B переменная S₁ автоматически обращается в нуль и, следовательно, становится небазисной переменной. Таким образом , между множеством небазисных и множеством базисных переменных происходит взаимообмен переменными X₂ и S₁ . Этот процесс можно наглядно представить в виде следующей таблицы.

Экстремальная точка	Нулевые переменные	Ненулевые переменные
А	S2 , X2	S1 , X1
В	S1 , X2	S2 , X1

Применяя аналогичную процедуру ко всем экстремальным точкам, можно убедиться в том, что любую последующую экстремальную точку всегда можно определить путем взаимной замены по одной переменной в составе базисных и небазисных переменных (предыдущей смежной точки). Этот фактор существенно упрощает реализацию вычислительных процедур симплекс-метода.

Рассмотренный процесс взаимной замены переменных приводит к необходимости введения двух новых терминов. Включаемой переменной называется небазисная в данный момент переменная, которая будет включена в множество базисных переменных на следующей итерации (при переходе к смежной экстремальной точке). Исключаемая переменная — это та базисная переменная, которая на следующей итерации подлежит исключению из множества базисных переменных.

Вычислительные процедуры симплекс-метода.

 симплекс-алгоритм состоит из следующих шагов.

Шаг 0. Используя линейную модель стандартной формы, определяют начальное допустимое базисное решение путем приравнивания к нулю п — т (небазисных) переменных.

Шаг 1. Из числа текущих небазисных (равных нулю) переменных выбирается включаемая в новый базис переменная, увеличение которой обеспечивает улучшение значения целевой функции. Если такой переменной нет, вычисления прекращаются, так как текущее базисное решение оптимально. В противном случае осуществляется переход к шагу 2.

Шаг 2. Из числа переменных текущего базиса выбирается исключаемая переменная, которая должна принять нулевое значение (стать небазисной) при введении в состав базисных новой переменной.

Шаг 3. Находится новое базисное решение, соответствующее новым составам небазисных и базисных переменных. Осуществляется переход к шагу 1.

Поясним процедуры симплекс-метода на примере решения нашей задачи. Сначала необходимо представить целевую функцию и ограничения модели в стандартной форме:

Z -    X1    -    25X2 +0S₁ -0S₂ =   0 (Целевая функция)

5X1  +  100X2 +  S1           = 1000 (Ограничение)

-X1    +     2X2          + S2 = 0 (Ограничение)

Как отмечалось ранее, в качестве начального пробного решения используется решение системы уравнений, в которой две переменные принимаются равными нулю. Это обеспечивает единственность и допустимость получаемого решения. В рассматриваемом случае очевидно, что подстановка X1 = X2 = 0 сразу же приводит к следующему результату: S1 = 1000, S2 = 0 (т. е. решению, соответствующему точке А на рис. 1). Поэтому точку А можно использовать как начальное допустимое решение. Величина Z в этой точке равна нулю , так как и X1 и X2  имеют нулевое значение . Поэтому , преобразовав уравнение целевой функции так , чтобы его правая часть стала равной нулю , можно убедиться в том , что правые части уравнений целевой функции и ограничений полностью характеризуют начальное решение . Это имеет место во всех случаях , когда начальный базис состоит из остаточных переменных.

Полученные результаты удобно представить в виде таблицы:

Базисные переменные	Z	X1	X2	S1	S2	Решение
Z	1	-1	- 25	0	0	0	Z - уравнение
S1	0	5	100	1	0	1000	S1 -уравнение
S2	0	-1	2	0	1	0	S2 - уравнение

Эта таблица интерпретируется следующим образом. Столбец “Базисные переменные” содержит переменные пробного базиса S1, S2,  значения которых приведены в столбце “Решение”. При этом подразумевается, что небазисные переменные X1 и X2 (не представленные в первом столбце) равны нулю. Значение целевой функции

Z = 1*0 + 25*0 + 0*1000 + 0*1 равно нулю, что и показано в последнем столбце таблицы.

Определим, является ли полученное пробное решение наилучшим (оптимальным). Анализируя Z - уравнение, нетрудно заметить, что обе небазисные переменные X1 и X2, равные нулю, имеют отрицательные коэффициенты. Всегда выбирается переменная с большим абсолютным значением отрицательного коэффициента, так как практический опыт вычислений показывает, что в этом случае оптимум достигается быстрее.

Это правило составляет основу используемого в вычислительной схеме симплекс-метода условия оптимальности, которое состоит в том, что, если в задаче максимизации все небазисные переменные в Z -  имеют неотрицательные коэффициенты, полученное пробное решение является оптимальным. В противном случае в качестве новой базисной переменной следует выбрать ту , которая имеет наибольший по абсолютной величине отрицательный коэффициент. Применяя условие оптимальности к исходной таблице, выберем в качестве переменной, включаемой в базис, переменную Х2. Исключаемая переменная должна быть выбрана из совокупности базисных переменных S1 , S2 . Процедура выбора исключаемой переменной предполагает проверку условия допустимости, требующего, чтобы в качестве исключаемой переменной выбиралась та из переменных текущего базиса, которая первой обращается в нуль при увеличении включаемой переменной X2 вплоть до значения, соответствующего смежной экстремальной точке.

Интересующее нас отношение (фиксирующее искомую точку пересечения и идентифицирующее исключаемую переменную) можно определить из симплекс-таблицы. Для этого в столбце, соответствующем вводимой переменной X2 , вычеркиваются отрицательные и нулевые элементы ограничений. Затем вычисляются отношения постоянных, фигурирующих в правых частях этих ограничений , к оставшимся элементам столбца , соответствующего вводимой переменной X2 . Исключаемой переменной будет та переменная текущего базиса , для которой указанное выше отношение минимально.

Начальная симплекс-таблица для нашей задачи, получаемая после проверки условия допустимости (т. е. после вычисления соответствующих отношений и определения исключаемой переменной), воспроизведена ниже. Для удобства описания вычислительных процедур, осуществляемых на следующей итерации, введем ряд необходимых определений. Столбец симплекс-таблицы , ассоциированный с вводимой переменной , будем называть ведущим столбцом . Строку , соответствующую исключаемой переменной , назовем ведущей строкой ( уравнением ) , а элемент таблицы , находящийся на пересечении ведущего столбца и ведущей строки , будем называть ведущим элементом .

После того как определены включаемая и исключаемая переменные (с использованием условий оптимальности и допустимости), следующая итерация (поиск нового базисного решения) осуществляется методом исключения переменных, или методом Гаусса — Жордана. Этот процесс изменения базиса включает вычислительные процедуры двух типов.

Тип 1 (формирование ведущего уравнения).

Новая ведущая строка = Предыдущая ведущая строка / Ведущий элемент

Тип 2 (формирование всех остальных уравнений, включая Z - уравнение).

Новое уравнение = Предыдущее уравнение —



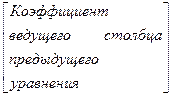
*(Новая ведущая строка).

Выполнение процедуры типа 1 приводит к тому, что в новом ведущем уравнении ведущий элемент становится равным единице. В результате осуществления процедуры типа 2 все остальные коэффициенты, фигурирующие в ведущем столбце, становятся равными нулю. Это эквивалентно получению базисного решения путем исключения вводимой переменной из всех уравнений, кроме ведущего. Применяя к исходной таблице процедуру 1 , мы делим S2 - уравнение на ведущий элемент, равный 1 .

Базисные переменные	Z	X1	X2	S1	S2	Решение
Z
S1
S2	0	-1/2	1	0	1/2	0

Чтобы составить новую симплекс-таблицу, выполним необходимые вычислительные процедуры типа 2 .

1. Новое Z - уравнение.

старое Z - уравнение: (1   -1      -25    0    0     0)

                     (- (-25) * (0   -1/2     1     0   1/2    0)

                                        (1   -13¹/₂   0     0  12¹/₂  0)

2.   Новое S₁ - уравнение

     старое S₁ - уравнение: (0    5   100   1     0    1000)

                           ( - 100) *    (0   -¹/₂   1      0    ¹/₂       0)

                                               ( 0   55    0     1   -50   1000)      

        

Новая симплекс-таблица будет иметь вид:

             

Базисные переменные	Z	X1	X2	S1	S2	Решение
Z	1	-131/2	0	0	121/2	0	Z - уравнение
S1	0	55	0	1	-50	1000	S1 -уравнение
X2	0	-1/2	1	0	1/2	0	X2 - уравнение

В новом решении X₁ = 0 и S₂ = 0 . Значение Z не изменяется.

Заметим, что новая симплекс-таблица обладает такими же характеристиками, как и предыдущая: только небазисные переменные X₁ и S₂ равны нулю, а значения базисных переменных, как и раньше, представлены в столбце “ Решение ”. Это в точности соответствует результатам , получаемым при использовании метода Гаусса—Жордана .

Из последней таблицы следует, что на очередной итерации в соответствии с условием оптимальности в качестве вводимой переменной следует выбрать X₁ ,так как коэффициент при этой переменной в Z- уравнений равен -13¹/₂ . Исходя из условия, определяем, что исключаемой переменной будет S₁. Отношения, фигурирующие в правой части таблицы, показывают, что в новом базисном решении значение включаемой переменной X₁ будет равно ¹⁰⁰⁰/₅₅ ( = минимальному отношению). Это приводит к увеличению целевой функции на ( ¹⁰⁰⁰/₅₅ ) *    (   -13^1/₂ ) = ( 245⁵/₁₁ ) .

К получению симплекс-таблицы, соответствующей новой итерации, приводят следующие вычислительные операции метода Гаусса—Жордана.

1)  Новое ведущее  S₁ - уравнение = Предыдущее S₁ - уравнение / (55) .

Базисные переменные	Z	X1	X2	S1	S2	Решение
Z
S1	0	1	0	1/55	- 50/55	1000/55
X2

2) Новое  Z - новое = Предыдущее  Z - уравнение - (-13¹/₂) * Новое /ведущее уравнение:

                                         ( 1   -13¹/₂  0     0     12¹/₂       0)

                    - ( -13¹/₂) *  (0      1     0    ¹/₅₅   -⁵⁰/₅₅    ¹⁰⁰⁰/₅₅₎

                                         ( 1      0     0    ²⁷/₁₁₀   ⁵/₂₂   245⁵/₁₁)

3) Новое X₂ - уравнение = Предыдущее  X₂ - уравнение - (-¹/₂) * Новое ведущее уравнение:

                                               ( 0  -¹/₂   1     0       ¹/₂        0)

                         - ( - ¹/₂) *     (0    1     0    ¹/₅₅  -⁵⁰/₅₅    ¹⁰⁰⁰/₅₅)

                                         ( 0    0     1   ¹/₁₁₀    ¹/₂₂     9¹/₁₁₎

В результате указанных преобразований получим следующую симплекс-таблицу.

Базисные переменные	Z	X1	X2	S1	S2	Решение
Z	1	0	0	27/110	5/22	2455/11
X1	0	1	0	1/55	-50/55	1000/55
X2	0	0	1	1/110	1/22	91/11

В новом базисном решении X₁=¹⁰⁰⁰/₅₅ и X₂=9¹/₁₁ . Значение Z увеличилось с 0 (предыдущая симплекс-таблица) до 245⁵/₁₁  (последняя симплекс-таблица). Этот результирующий прирост целевой функции  обусловлен увеличением X₁ от О до ¹⁰⁰⁰/₅₅ , так как из Z - строки предыдущей симплекс-таблицы следует , что возрастанию данной переменной на единицу соответствует увеличение целевой функции на( -13¹/₂ ) .

Последняя симплекс-таблица соответствует оптимальному решению задачи, так как в Z - уравнении ни одна из небазисных переменных не фигурирует с отрицательным коэффициентом. Получением этой результирующей таблицы и завершаются вычислительные процедуры симплекс-метода.

В рассмотренном выше примере алгоритм симплекс-метода использован при решении задачи, в которой целевая функция подлежала максимизации. В случае минимизации целевой функции в этом алгоритме необходимо изменить только условие оптимальности: в качестве новой базисной переменной следует выбирать ту переменную, которая в Z - уравнении имеет наибольший положительный коэффициент. Условия допустимости в обоих случаях ( максимизации и минимизации ) одинаковы . Представляется целесообразным дать теперь окончательные формулировки обоим условиям , используемым в симплекс-методе .

Условие оптимальности. Вводимой переменной в задаче максимизации (минимизации) является небазисная переменная , имеющая в Z -уравнении наибольший отрицательный (положительный) коэффициент , В случае равенства таких коэффициентов для нескольких небазисных переменных выбор делается произвольно , если все коэффициенты при небазисных переменных в Z - уравнении неотрицательны (неположительны), полученное решение является оптимальным.

Условие допустимости, в задачах максимизации и минимизации в качестве исключаемой переменной выбирается та базисная переменная, для которой отношение постоянной в правой части соответствующего ограничения к (положительному) коэффициенту ведущего столбца минимально. В случае равенства этого отношения для нескольких базисных переменных выбор делается произвольно.

Оптимальное решение

С точки зрения практического использования результатов решения задач ЛП классификация переменных, предусматривающая их разделение на базисные и небазнсные, не имеет значения и при анализе данных, характеризующих оптимальное решение, может не учитываться. Переменные, отсутствующие в столбце “Базисные переменные ”, обязательно имеют нулевое значение. Значения остальных переменных приводятся в столбце “Решение”. При интерпретации результатов оптимизации в нашей задаче нас, прежде всего, интересует количество времени, которое закажет наша фирма на радио и телевидение,  т. е. значения управляемых переменных X₁ и X₂ . Используя данные, содержащиеся в симплекс-таблице для оптимального решения, основные результаты можно представить в следующем виде:

Управляемые переменные	Оптимальные значения	Решение
X1	1000/55	Время, выделяемое фирмой на телерекламу
X2	91/11	Время, выделяемое фирмой на радиорекламу
Z	2455/11	Прибыль, получаемая от рекламы.

Заметим, что Z = X₁ + 25X₂ = ¹⁰⁰⁰/₅₅ + 25 * 9¹/₁₁ = 245⁵/₁₁ . Это решение соответствует данным заключительной симплекс-таблицы.

 

Табличный метод.

Обозначим через 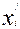,  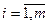базисные переменные, а через 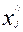,  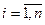свободные. Выразив целевую функцию и базисные переменные через свободные, сформулируем задачу в следующем виде: максимизировать 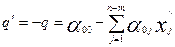  (7) при условных 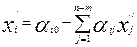, ,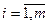, 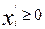  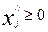(8). Тогда задачу можно представить следующей матрицей:

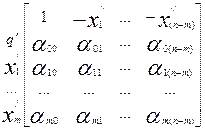  (9)

Замечая, что столбец коэффициентов α_{i 0}, i≠0 представляет собой базисное решение при базисе 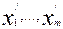, а строка α_0j, j≠0 представляет собой взятые с обратным знаком коэффициенты при свободных переменных в выражении q^/, приходим к выводу, что базисное решение допустимо если α_{i 0}≥0, i≠0. Если α_0j≥0, j≠0, то она является и оптимальной. При оптимальном базисном решении .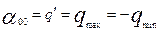

Рассмотрим наш пример:

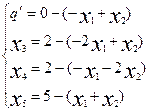
Матрица коэффициентов в виде таблиц:

а)

	1
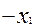
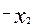
q/	0    2	-1     1	1     -2
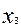
	2    4	-2     2	1     -4
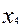
	2    2	1     -1	-2    -2
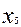
	5   -2	1     -1	1     2

б)

	1
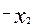
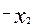
q/	2     1	1   -1/3	1   -1/2
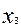
	6     3	2     -1	3      1
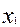
	2     2	1   -2/3	-2   2/3
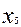
	3     1	-1  -1/3	-1  -1/3

в)

	1
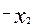
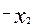
q/	3	2/3	1/3
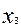
	9	1	1
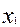
	4	1/3	2/3
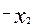
	1	-1/3	1/3

т.к α_0i отрицательно, то оптимум не найден, значит переменную х, следует сделать базисной. Если отрицательными окажутся α_0j при нескольких свободных переменных, то в базисном можно переводить любую из них.

Определим каждую из базисных переменных. Нужно сделать свободной ту, которая быстрее обратится в нуль при увеличении х₁. Это будет та базисная переменная х_i, для которой коэффициенты в столбце α_i1>0 и отношение 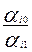 наименьшее. Это переменная х_n.

Коэффициент α_i1 стоящий на пересечении столбца х₁ и строки x_n назовем генеральным. Пусть 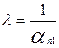  λ =1 выделим коэффициенты, стоящие на строке х₁ и столбце x_n. Теперь заполним нижние правые углы клеток:

1)     в клетку α_i1 заполняем λ.

2)     в клетках выделенной строки записываем верхние коэффициенты, умноженные на + λ.

3)     В клетках выделенного столбца записываем верхние коэффициенты, умноженные на - λ.

4)     В остальных клетках записываем произведение выделенных коэффициентов, на пересечении которого стоит данная клетка.

Заполним таблицу Б:

1)     Строку и столбец соответствующие новым свободной и базисной переменой, заполняем нижними коэффициентами выделенной строки и столбца таблицы а.

2)     В остальные клетки записываем суммы коэффициентов стоящих в соответствующих клетках таблицы а.

Оптимальное решение не найдено – повторим процедуру, заполняя таблицу b. Теперь коэффициенты α_0j, j≠0 положительны, и она даёт оптимальное решение, которое находим по столбцу свободных членов: x₁=4; x₂=1; x₃=9; x₄=x₅=0; ; .

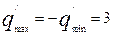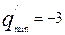Получение начального допустимого базисного решения.

Общий вид системы управлений имеющей допустимое базисное решение 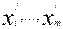, получим и (7), переписав его:

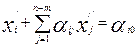; α_i0≥0, 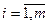.  (10)

Здесь каждая переменная, 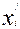 принятая за базисную входит только в одно из уравнений с коэффициентом «+1». Если такие переменные найдутся в каждом из уравнений системы (1), то они и составят первоначальный допустимый базис.

Если в некоторых уравнениях таких переменных нет, то поступаем так. Выписываем уравнения с переменными, которые можно принять за базисные. Обозначим их 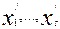. В остальных m-s уравнениях вводим искусственные базисные переменные 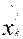, k=s+1,…m 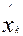≥0.

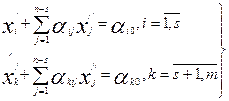  (11)

Чтобы полученная система совпадала с исходной в окончательном решении 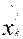 должны обратится в нуль. Для того их вводят в выражения для q^/ с достаточно большими коэффициентами.

Двойственная задача.

Двойственная задача – это вспомогательная задача линейного программирования, формируемая с помощью определенных правил непосредственно из условий исходной, или прямой, задачи. В основу формулировки положен тот факт, что использование симплекс-метода требует приведения любой задачи линейного программирования к линейной форме.

Двойственная задача в соответствии со следующими правилами:

1.    Каждому ограничению прямой задачи соответствует переменная двойственной задачи;

2.    Каждой переменной прямой задачи соответствует ограничение двойственной задачи;

3.    Коэффициенты при некоторой переменной, фигурирующие в ограничениях прямой задачи становятся коэффициентами левой части соответствующего ограничения двойственной задачи, а коэффициент, фигурирующий при той же переменной в выражении для целевой функции прямой задачи становится постоянной правой части этого же ограничения двойственной задачи. Из указанного правила построения двойственной задачи следует, что она имеет m переменных (y₁, y₂, … y_m) и n ограничений (соответствующих n переменным прямой задачи x₁, x₂, … x_n).

Пусть в прямой задаче имеем свободные переменные х₁,…, х_i и задача сформулирована в виде: максимизировать 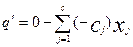 при условиях: 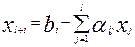, 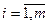.  (12)

Этой задаче соответствует матрица:

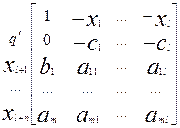  (13)

В двойственной задаче за свободные переменные выберем u₁,…, u_m и сформулируем её в виде: минимизировать: 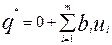  (14) при условиях: 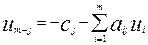, 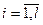.  (15). Этой задаче соответствует матрица вида:

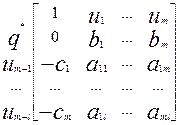  (16)

Как видим, матрица (13)- транспонированная матрица (16), значит прямая, и двойственная задача могут быть описаны одной матрицей, однако между прямыми и двойственными переменными должно быть установлено соответствие:

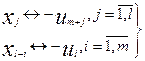.  (17)

Если в матрице заданы положительные элементы первой строки, и первого столбца, то матрица соответствует оптимальному решению как прямой, так и двойственной задаче. При этом .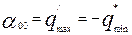

Список используемой литературы.

• Ашманов С.А., «Линейное программирование», Москва, 1961 г.
• Коршунов Ю.М., «Математические основы кибернетики», Москва, 1987 г.;