Министерство общего и профессионального образования
Российской Федерации
Южно-Уральский Государственный Университет
Кафедра АиУ.
Реферат
по математическим основам теории систем
НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Выполнил:
Подрезов Сергей Валерьевич
Группа:
ПС-243
Преподаватель:
Разнополов Олег Александрович
Челябинск, 2005
Содержание.
Введение. 3
Необходимые
и достаточные условия существования экстремума. 3
Итеративные методы. Постановка задачи. 7
Пример. 8
Список используемой литературы. 10
Введение.
Классическая теория оптимизации
основана на использовании дифференциального исчисления для нахождения точек
максимума и минимума (экстремумов) функции в условиях наличия и отсутствия
ограничений.
Постановка задачи нелинейного программирования
В задаче нелинейного
программирования (НЛП) требуется найти значение многомерной переменной 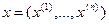 , минимизирующее целевую функцию
, минимизирующее целевую функцию 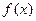 при условиях, когда на
переменную
при условиях, когда на
переменную  наложены ограничения
типа неравенств, а переменные
наложены ограничения
типа неравенств, а переменные 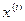 , то есть компоненты вектора
, то есть компоненты вектора 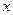 , неотрицательны. Если некоторые ограничения входят в задачу
со знаком равенства, например,
, неотрицательны. Если некоторые ограничения входят в задачу
со знаком равенства, например, 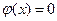 то их можно
представить в виде пары неравенств
то их можно
представить в виде пары неравенств 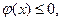
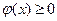 , сохранив тем самым типовую формулировку задачи.
, сохранив тем самым типовую формулировку задачи.
Необходимые и достаточные условия существования экстремума.
Рассмотрим условия существования
экстремумов функции и переменных 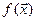 , предполагая, что первая и вторая производные
, предполагая, что первая и вторая производные 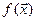 непрерывны.
непрерывны.
Теорема 1:
Если точка 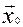 является экстремальной
точкой функции
является экстремальной
точкой функции 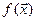 , то
, то 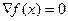 .
.
Если 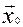 - точка максимума
(минимума), то
- точка максимума
(минимума), то 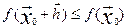 (
(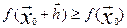 ), для всех
), для всех  при малых hj.
при малых hj.
По теореме Тейлора при 0≤Θ≤1 верно
разложение 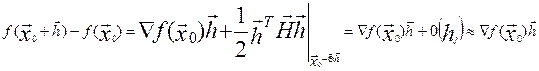 .
.
Предположим, что 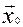 - точка минимума.
Предположим, что
- точка минимума.
Предположим, что 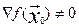 , тогда для некоторого j
, тогда для некоторого j 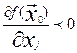 , либо
, либо 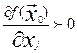 .
.
Выберем знак 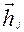 так, чтобы
так, чтобы 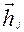
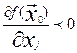 , остальные
, остальные 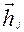 =0. Тогда получим, что
=0. Тогда получим, что  , что противоречит определению точки минимума. Значит,
, что противоречит определению точки минимума. Значит, 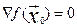 .
.
Это условие является необходимым,
но не достаточным. Точки, удовлетворяющие условие 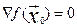 будем называть
стационарными.
будем называть
стационарными.
Теорема 2:
Стационарная точка 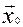 является
экстремальной, когда матрица Гессе Н в точки
является
экстремальной, когда матрица Гессе Н в точки 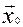 оказывается, определена
положительно (т. минимума) или отрицательно (т. максимума).
оказывается, определена
положительно (т. минимума) или отрицательно (т. максимума).
Из предыдущей теоремы: 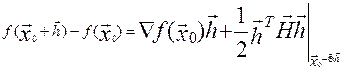 . Пусть
. Пусть  - точка минимума,
тогда по определению
- точка минимума,
тогда по определению 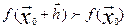 .
.
Для всех ненулевых 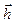 , это означает, что
, это означает, что 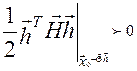 , т.к.
, т.к. 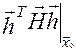 - квадратичная форма,
то рассматриваемая величина положительна тогда и только тогда, когда
- квадратичная форма,
то рассматриваемая величина положительна тогда и только тогда, когда 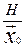 - положительно определенная
матрица.
- положительно определенная
матрица.
Матрица Гессе 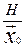 - матрица с элементами
- матрица с элементами
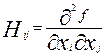 . Если
. Если 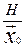 неопределенна, то
неопределенна, то 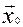 - седловая точка.
- седловая точка.
Если 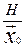 полуопределена, то в
точке может быть экстремум, но для установления этого нужно рассматривать члены
разложения в ряд Тейлора более высокого порядка. В некоторых случаях можно
сделать вывод об отсутствии экстремума. Сформулируем теорему для f(g) одной переменой.
полуопределена, то в
точке может быть экстремум, но для установления этого нужно рассматривать члены
разложения в ряд Тейлора более высокого порядка. В некоторых случаях можно
сделать вывод об отсутствии экстремума. Сформулируем теорему для f(g) одной переменой.
Теорема 3:
Если в стационарной точке у0 первые (n-1) производные f(y) равны 0, а f(n)(y)≠0, то при y=y0 функция:
1) Имеет
точку перегиба, если h
- нечетное,
2) Экстремальную
точку, если h - четное.
При 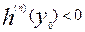 - максимум, а при
- максимум, а при 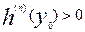 - минимум.
- минимум.
Ограничения в виде равенств.
1)
Метод
Якоби (приведённого градиента).
Данный метод является обобщенный
симплекс метод линейного программирования. Рассмотрим задачу минимизирования z=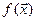 при ограничениях
при ограничениях 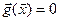 где
где 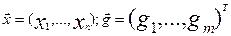 , а функция
, а функция 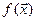 и
и 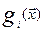 дважды не прерывно
дифференцируемы.
дважды не прерывно
дифференцируемы.
Идея заключается в том, чтобы
найти аналитическое выражение для первых частных производных функций 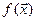 , во всех точках удовлетворяющих
, во всех точках удовлетворяющих 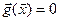 .
.
Из теоремы Тейлора следует, что
для точки 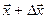 можно записать:
можно записать:
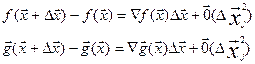
При ∆xj→0 имеем:

т.к. 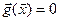 , то
, то 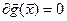 , значит
, значит
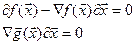 (1)
(1)
Пусть 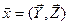 , где
, где 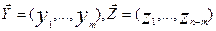 являются зависимыми и
независимыми переменными (m<n), образующими вектор
являются зависимыми и
независимыми переменными (m<n), образующими вектор 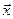 . Градиенты имеют вид:
. Градиенты имеют вид:
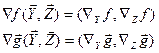
Введём определение двух матрицу:
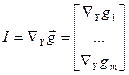 (2)
(2)
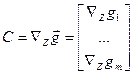 (3)
(3)
Матрицу 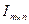 называют матрицей
Якоби, а
называют матрицей
Якоби, а 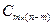 матрицей управления.
матрицей управления.
Перепишем (1):
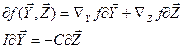 (4)
(4)
Далее: т.к. 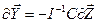 , то
, то 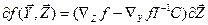 (5)
(5)
 , (6)
, (6)
где 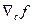 - проведенный
градиент. Вектор
- проведенный
градиент. Вектор 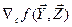 должен обратятся в
нуль в стационарных точках. При этом элементы матрицы Гессе соответствуют
компонентам вектора независимых переменных
должен обратятся в
нуль в стационарных точках. При этом элементы матрицы Гессе соответствуют
компонентам вектора независимых переменных 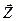 . Вектор
. Вектор 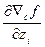 задаёт i-ю строку матрице Гессе Нс.
задаёт i-ю строку матрице Гессе Нс.
2)
Метод
множителей Лагранжа
Пусть 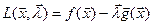 .
.
Функция L называется функцией Лагранжа, а
параметры  множителями Лагранжа.
Без доказательства приведем утверждение, что в стационарной точке Y0 верно равенство:
множителями Лагранжа.
Без доказательства приведем утверждение, что в стационарной точке Y0 верно равенство:
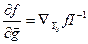
Пусть 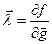 , откуда
, откуда 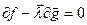 . Это уравнение выражает условие стационарности точек. В
более удобном виде
. Это уравнение выражает условие стационарности точек. В
более удобном виде
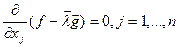 .
.
Применительно к функциям Лагранжа
эти условия стационарности имеют вид
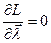 и
и 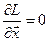 .
.
Это означает, что задача оптимизации 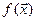 при
при 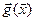 эквивалентна задаче
нахождения безусловного экстремума функции Лагранжа
эквивалентна задаче
нахождения безусловного экстремума функции Лагранжа 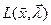 .
.
Ограничения в виде неравенств.
1. Обобщённый метод множителей Лагранжа.
Пусть дана задача максимизировать
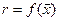 при ограничениях
при ограничениях 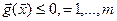 .
.
1) Решить
задачу без учёта ограничений. Если полученная точка удовлетворяет все ограничения,
то прекратить вычисления, иначе - положить k=1 и продолжить.
2) Сделать
любые k ограничений
активными (превратить в равенства) и найти оптимум при этих ограничениях. Если
найденная точка удовлетворяет оставшимся ограничениям, то локальный оптимум
найден. Иначе, увеличим k
и повторяем 2). Если все k
ограничений были активными, то переходим к 3).
3) Допустимых
решений не существует.
2. Условия Кука – Таккера.
Рассмотрим ту же задачу.
Ограничения – неравенство можно преобразовать к виду равенств, введя
соответствующие неотрицательные переменные 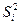 , которые прибавили к левым частям i-x ограничений.
, которые прибавили к левым частям i-x ограничений.
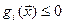 . Пусть
. Пусть  .
.
При этом функция Лагранжа
записывается в виде 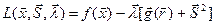 .
.
В задаче максимизации
(минимизации) необходимым условием оптимальности является неотрицательность
(неположительность)  .
.
Прировняем частные производные L к 0:
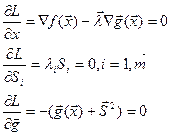
Из этих уравнений следует
необходимые условия Кука – Таккера, которые должны удовлетворять 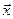 и
и  , определяющие стационарную точку в задаче оптимизации
, определяющие стационарную точку в задаче оптимизации
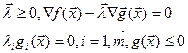
Для минимизации  . Если ограничения заданы в виде равенств, то на знак
. Если ограничения заданы в виде равенств, то на знак  ограничения не накладываются.
ограничения не накладываются.
3. Достаточность условий Кука – Таккера.
Необходимые условия Кука –
Таккера являются также достаточными, если целевая функция и область допустимых
значений обладают определенными свойствами:
|
Типы
оптимизации
|
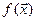
|
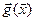
|
λi
|
|
Максимизация
|
Вогнутая
|
|
≥0 1 ≤ i ≤ r
≤0 r+1 ≤ i
≤ p
без огр.
p+1 ≤ i ≤ m
|
|
Минимизация
|
Выпуклая
|
|
≤0 1 ≤ i ≤ r
≥0 r+1 ≤ i
≤ p
без огр.
p+1 ≤ i ≤ m
|
Ограничения задаются в виде:
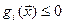 i = 1,…, r,
i = 1,…, r,
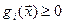 i = r+1,…, p,
i = r+1,…, p,
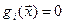 i = p+1,…, m.
i = p+1,…, m.
Функция Лагранжа:
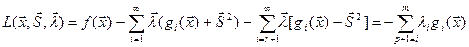
4. Квадратичное
программирование.
Модель квадратичного
программирования определяется, как максимизировать (минимизировать) 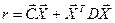 при ограничениях
при ограничениях 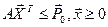 , где
, где 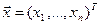 ,
, 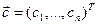 ,
, 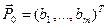 ,
, 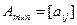 ,
, 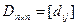 .
.
Матрица D квадратичной формы предполагается
отрицательно (положительно) определённой в задаче максимизации (минимизации).
Решение получается путём применения условий Кука – Таккера: 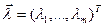 и
и 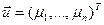 - множители Лагранжа:
- множители Лагранжа:
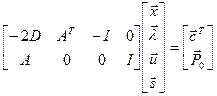 ,
,
где 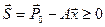 - вектор дополнительных
переменных.
- вектор дополнительных
переменных.
Итеративные методы. Постановка задачи.
Ограниченные возможности
симплексного метода привели к широкому распространению градиентных и других
итеративных методов, в основе которых лежит понятие градиента целевой функции g(x).
Градиентом функции g(x), обозначаемым grad g(x) и 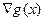 , называют вектор, величина которого определяет скорость изменения
функции g(x), и наибольшего возрастания
этой функции. Пусть
, называют вектор, величина которого определяет скорость изменения
функции g(x), и наибольшего возрастания
этой функции. Пусть 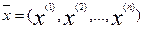 , но
, но 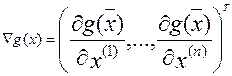 . (1)
. (1)
Условия стационарности точки 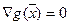 . (2) Разложим
. (2) Разложим 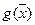 в ряд Тейлора в
окрестности точки оптимума
в ряд Тейлора в
окрестности точки оптимума 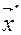 , которую считаем стационарной
, которую считаем стационарной 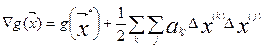 (3), где
(3), где 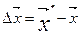 - отклонение от точки
оптимума;
- отклонение от точки
оптимума; 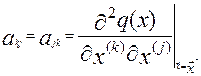 (4), т.к.
(4), т.к. 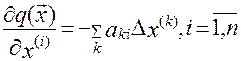 , то
, то
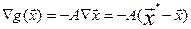 , (5) где элементы матрицы
А определяются akj по формуле (4).
Разрешая систему уравнений (5) относительно
, (5) где элементы матрицы
А определяются akj по формуле (4).
Разрешая систему уравнений (5) относительно 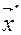 , получаем:
, получаем: 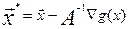 . (6) Если заменить
неизвестную матрицу А-1 на матрицу Г ([γkj]), то можно
надеется, что величина
. (6) Если заменить
неизвестную матрицу А-1 на матрицу Г ([γkj]), то можно
надеется, что величина 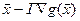 даст значение, более
близкое к оптимуму, чем x.
При этом открываются возможности многошаговой процедуры поиска.
даст значение, более
близкое к оптимуму, чем x.
При этом открываются возможности многошаговой процедуры поиска.
Обозначим через 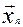 , значение
, значение 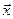 на n-ом шаге. Тогда процедура поиска запишется
в виде
на n-ом шаге. Тогда процедура поиска запишется
в виде 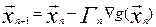 .
.
Градиентный метод.
Этот метод представляет собой
последовательность шагов, содержащих две операции:
1) Определение
направления наибольшей крутизны спуска, т.е направление антиградиента g(x).
2) Перемещение
в выбранном направлении на заданное расстояние.
Математически
стратегия градиентного метода получается, если перемещение на каждом шаге 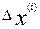 будет пропорционально
составляющей градиента в направлении этой оси:
будет пропорционально
составляющей градиента в направлении этой оси: 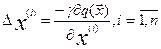 (8) тогда Гn будет диагональной Гn =γI (9) при этом, поправка на n-м шаге равна:
(8) тогда Гn будет диагональной Гn =γI (9) при этом, поправка на n-м шаге равна: 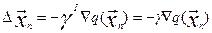 . (10) При таком
ограничении некоторые шаги могут оказаться мелкими. Это можно исправить,
используя стратегию с постоянным шагом γ.
. (10) При таком
ограничении некоторые шаги могут оказаться мелкими. Это можно исправить,
используя стратегию с постоянным шагом γ. 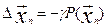 (11) где
(11) где 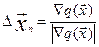 .
.
Метод наискорейшего спуска (подъема).
В этом методе градиент находят
только в начальной точке и движении в найденном направлении продолжается c одинаковыми шагами до тех
пор, пока уменьшается значение 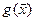 . Если на каком-то шаге
. Если на каком-то шаге 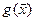 возросло, то движение
в данном направлении прекращается, последний шаг снимается полностью, или на
половину, и вычисление нового градиента функции
возросло, то движение
в данном направлении прекращается, последний шаг снимается полностью, или на
половину, и вычисление нового градиента функции 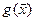 , т. е новое направление движение.
, т. е новое направление движение.
При этом, шаг движения не должен
быть большим, чтобы не пропустить оптимум на данном направлении.
Алгоритм Ньютона.
Этот метод применим, когда поверхность отклика достаточно
хорошо описывается уравнением 2-го порядка. Метод позволяет резко уменьшить
число шагов. При хорошей поверхности отклика вторые производные: 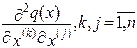 (12) вычисленные в
точки
(12) вычисленные в
точки 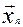 будут близкими и
элементам akj матрицы А. Используя в качестве
Гn матрицу вторых производных
будут близкими и
элементам akj матрицы А. Используя в качестве
Гn матрицу вторых производных 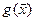 в точке
в точке 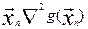 , получим вектор поправок для алгоритма Ньютона:
, получим вектор поправок для алгоритма Ньютона: 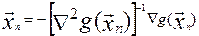 . (13) Если разложения
(3) является точным, то оптимум достигается за один шаг.
. (13) Если разложения
(3) является точным, то оптимум достигается за один шаг.
Пример.
Задача "О почтовой посылке": найти ее максимальный объем при
ограничении на обхват и длину.
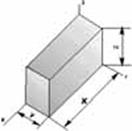
Постановка (формализация задачи)
Формулируем цель:
s=xyz->max
и ограничения:
x+2y+2z < 72,
0< x,y,z.
Задача является смешанной. ЦФ s -нелинейная, а область ограничений -
линейная. Область ограничений - многогранник, ограниченный координатными
плоскостями x,y,z и плоскостью x/72+y/36+z/36=1.
Т.к. значения x,y,z должны быть больше нуля и точка, определяющая максимум
ЦФ, должна лежать на поверхности многогранника, то заключаем, что положения
точки, обеспечивающей максимум ЦФ, возможны на грани р1-р3 многогранника
ограничений.
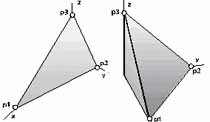
Алгоритм решения задачи.
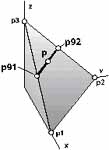
) В плоскости р1-р3 выполняем перебор точек р (возможные
сочетания переменных x,y,z) по формулам:
p=(1.-s11)*p91+s11*p92, 0 < s11 < 1,
где, р91, р92, в свою очередь, определяются:
p91=(1.-s12)*p1+s12*p3, 0 < s12 < 1,
p92=(1.-s12)*p2 +s12*p3, 0 < s12 < 1.
2) Вычисляем ЦФ s (s=x*y*z) при каждом сочетании x,y,z.
3) Сравниваем s с эталоном (регистром) s99. Как только s при расчете будет
больше s99, помещаем его в s99. В результате перебора (например, с помощью 2-го
цикла) и сравнения s c s99 (s > s99 ? s99=s) получаем s99 максимальное
из возможных s.
3) В момент достижения максимального значения s выполняем принудительный выход
из МК. Искомые значения x,y,z будут лежать в p.
4) Для контроля вычислений строим графики ЦФ в координатных плоскостях sx, sy,
sz (рис. 9, а,б.с или (рис. 9, д) непосредственно над плоскостью р1-р3 в
трехмерной координатной системе (аксонометрии) sxy.
Рис. Отображение ЦФ: s=x*y*z -> max на комплексном и
ортогональном чертежах а) полностью, б) до достижения максимума.
Список используемой литературы.
·
Таха Х., «Введение в исследование операций»,
Москва, 1985 г.;
·
Коршунов Ю.М., «Математические основы
кибернетики», Москва, 1987 г.;