Задача 1. В таблице 1 приведены следующие данные: единичная стоимость процесса добычи нефти и газа (Y), процент жидкости в добываемом из скважины газе (X) для различных месторождений.

1.                          В рамках линейной модели найдите регрессионную зависимость Y от Х.

2.                          Вычислите коэффициент корреляции между Х и Y.

3.                          Определите значимость регрессии для  a = 0,05.

4.                          Найдите 95% доверительные интервалы для параметров модели.

5.                          Найдите интервал, в котором с вероятностью 0,95 находится значение единичной стоимости добычи газа при наличии 25% жидкости.

6.                          Вычислите коэффициент детерминации R².

Исходные данные:

Х	Y
13.1	3.4
16.7	5.1
19.6	4.7
23.3	6.7
26.1	6.2
30.2	9.1
42.9	8.3

Решение:

1. Вычислим параметры уравнения линейной регрессии по формулам:

;  .

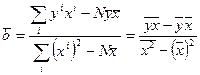Для этого организуем вычисления во вспомогательной таблице:

Номер	Х	Y	X2	Y2	XY
1	13.1	3.4	171.61	11.56	44.54
2	16.7	5.1	278.89	26.01	85.17
3	19.6	4.7	384.16	22.09	92.12
4	23.3	6.7	542.89	44.89	156.11
5	26.1	6.2	681.21	38.44	161.82
6	30.2	9.1	912.04	82.81	274.82
7	42.9	8.3	1840.41	68.89	356.07
Сумма	171.9	43.5	4811.21	294.69	1170.65
Среднее	24.6	6.2	687.3	42.1	167.2

Тогда

;

.

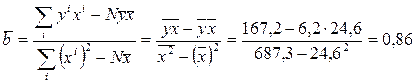Значит, уравнение линейной регрессии имеет вид

.

2. Вычислим коэффициент корреляции по формуле:

.

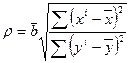Для применения формулы составим вспомогательную таблицу:

Номер	Х	Y		2
1	13.1	3.4	-11.5	132.25	-2.8	7.84
2	16.7	5.1	-7.9	62.41	-1.1	1.21
3	19.6	4.7	-5	25	-1.5	2.25
4	23.3	6.7	-1.3	1.69	0.5	0.25
5	26.1	6.2	1.5	2.25	0	0
6	30.2	9.1	5.6	31.36	2.9	8.41
7	42.9	8.3	18.3	334.89	2.1	4.41
Сумма	171.9	43.5		589.85		24.37

Тогда коэффициент корреляции найдется следующим образом:

.

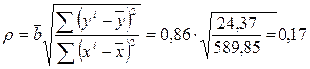3. Определим значимость регрессии для  a = 0,05, проверив гипотезу Н₀: «b=0», рассчитав статистику:

.

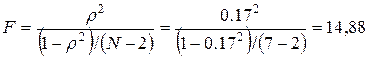По таблице F-статистики найдем критическое значение этого критерия:

.

Т.к. F>f_кр, то гипотезу Н₀: «b=0» отвергаем, т.е. регрессия значима.

4. Найдем 95%-ные доверительные интервалы для параметров модели. Для этого вначале найдем параметры распределения Стьюдента, оформив вспомогательную таблицу:

Номер	Х	Y
1	13.1	3.4	8.506	-5.106	26.07	-2.306	5.32
2	16.7	5.1	11.602	-6.502	42.28	-5.402	29.18
3	19.6	4.7	14.096	-9.396	88.28	-7.896	62.35
4	23.3	6.7	17.278	-10.578	111.89	-11.08	122.72
5	26.1	6.2	19.686	-13.486	181.87	-13.49	181.87
6	30.2	9.1	23.212	-14.112	199.15	-17.01	289.41
7	42.9	8.3	34.134	-25.834	667.40	-27.93	780.31
Сумма	171.9	43.5	128.514		1316.94		1471.16
Среднее	24.6	6.2	18.35914		188.13		210.17

Параметры двустороннего распределения Стьюдента:

;  .

Тогда, по таблице значений критерия Стьюдента, .

Тогда искомые доверительные интервалы:

Для коэффициента а:  .

Для коэффициента b:  .

5. Прогнозное значение .

При этом доверительный интервал для прогноза y(x) определяется границами:

, т.е. .

6.     Коэффициент детерминации

.

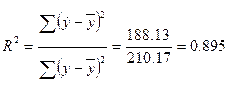Задача 2. Пусть b – оценка коэффициента наклона в регрессии Y на Х, а g – оценка коэффициента наклона в регрессии Х на Y. Покажите, что b = 1/g тогда и только тогда, когда R² = 1. В рамках линейной модели найдите регрессионную зависимость  Х от Y, пользуясь данными предыдущей задачи.

Решение: Используем обозначение Û – «тогда и только тогда»

R² = 1  Û  r = 1  Û 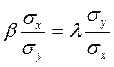   Û  b = 1/g.

Пояснения:

Коэффициент детерминации равен 1 тогда и только тогда, когда коэффициент корреляции равен 1. Коэффициент корреляции можно найти как с использованием b, так и с использованием g; приравняв эти формулы для вычисления коэффициента корреляции, получим утверждение b = 1/g.

Для нахождения регрессионной зависимости  Х от Y аналогично предыдущей задаче воспользуемся вспомогательной таблицей и формулами:

.

.

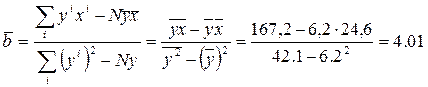Тогда искомое уравнение регрессии: .

Задача 3.  У семи сотрудников предприятия собраны данные об их среднемесячной зарплате (Y), возрасте (Х₁) и стаже работы (Х₂). С помощью метода наименьших квадратов оценить параметры линейной модели вида  влияния возраста и стажа работы на среднемесячную зарплату.

Исходные данные:

Х1	Х2	Y
35	6	1500
45	12	2100
20	3	1350
50	12	2100
30	2	1500
40	8	1800
25	2	1250

Решение:

Для подстановки числовых коэффициентов в систему уравнений, используемую в методе наименьших квадратов, составим вспомогательную таблицу:

	Х1	Х2	Y	Х12	Х22	Х1Х2	Y Х1	Y Х2
	35	6	1500	1225	36	210	52500	9000
	45	12	2100	2025	144	540	94500	25200
	20	3	1350	400	9	60	27000	4050
	50	12	2100	2500	144	600	105000	25200
	30	2	1500	900	4	60	45000	3000
	40	8	1800	1600	64	320	72000	14400
	25	2	1250	625	4	50	31250	2500
Сумма	245	45	11600	9275	405	1840	427250	83350
Квадрат суммы	60025	2025

Тогда система уравнений имеет вид:

.

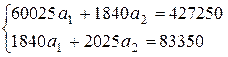С помощью пакета Excel – точнее, методом обратной матрицы с использованием функций МОБР и МУМНОЖ – найдем решение этой системы уравнений: а₁ = 6,02;  а₂ = 35,69.

Задача 4. Пользуясь данными задачи 3, построить линейную модель вида  влияния возраста и стажа работы на среднемесячную зарплату. Вычислите коэффициент детерминации R².

Решение:

Используя также вспомогательную таблицу из задачи 3, составим систему уравнений относительно коэффициентов модели:

.

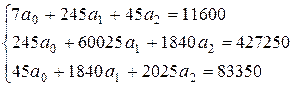Аналогично задаче 3 найдем оценки для параметров модели:

а₀ = 1611,46;  а₁ = 0,39;  а₂ = 5,0,   т.е. модель имеет вид:

Для применения формулы для нахождения коэффициента детерминации составим вспомогательную таблицу:

Номер	Х1	Х2	Y
1	35	6	1500	1655.14	155.14	24068.42	157.14	24693.88
2	45	12	2100	1689.04	-410.96	168888.1	-442.86	196122.4
3	20	3	1350	1634.29	284.29	80820.8	307.14	94336.73
4	50	12	2100	1690.99	-409.01	167289.2	-442.86	196122.4
5	30	2	1500	1633.19	133.19	17739.58	157.14	24693.88
6	40	8	1800	1667.09	-132.91	17665.07	-142.86	20408.16
7	25	2	1250	1631.24	381.24	145343.9	407.14	165765.3
Сумма			11600			621815.1		722142.9
Среднее			1657.14

Отсюда коэффициент детерминации:

.
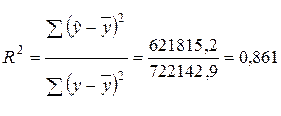