ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ
ИНСТИТУТ
Факультет Менеджмента и маркетинга
Кафедра «Экономико-математические методы и модели»
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Финансовая математика»
Вариант № 4
Исполнитель: Ходакова К.С.
Специальность: IV курс, Финансы и кредит,
день
№
зачетной книжки: 04ФФБ00884
Руководитель:.пр. Семененко
М.Г.
Калуга, 2008
Задание
1
Приведены поквартальные данные о кредитах от коммерческого банка на жилищное строительство (в условных
единицах) за 4 года (всего 16 кварталов).
Требуется:
1
Построить адаптивную мультипликативную модель Хольта-Уинтерса
с учетом сезонного фактора, приняв параметры сглаживания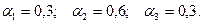 
2
Оценить точность построенной модели с использованием
средней относительной ошибки аппроксимации.
3
Оценить адекватность построенной модели на основе
исследования:
-
Случайности остаточной компоненты по критерию
пиков;
-
Независимости уровней ряда остатков по d-критерию (критические
значения d1=1,10
и d2=1,37) и
по первому коэффициенту автокорреляции при критическом значении r1=0,32;
-
Нормальности распределения остаточной компоненты
по R/S-критерию с критическими значениями от
3 до 4,21.
-
4
Построить точечный прогноз на 4 шага вперед, т.е. на 1
год.
5
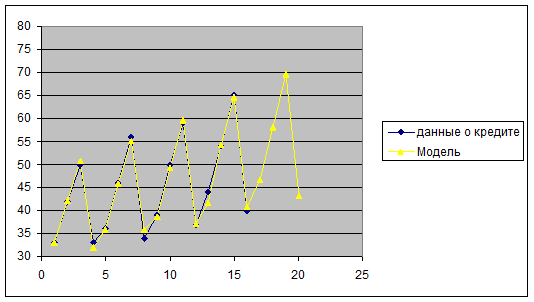
Отразить на графике фактические, расчетные и прогнозные
данные.
Решение:
1.
Таблица
1
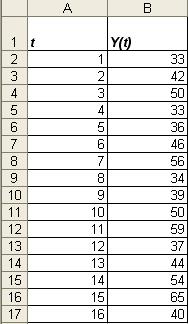
1
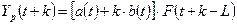Мультипликативная
модель Хольта-Уинтерса с линейным ростом имеет следующий вид:
k = 1, L
= 4
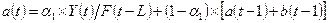Уточнение
коэффициентов модели производится с помощью формул:
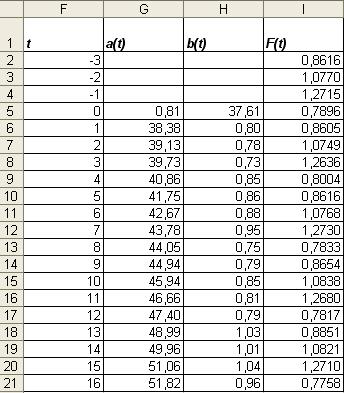
Для оценки начальных значений а(0) и b(0) применим линейную модель к первым 8
значениям Y(t)
из таблицы 1. а(0) находится с помощью функции НАКЛОН, b(0) с помощью функции ОТРЕЗОК в MS Excel.
а(0) = 0,81, b(0)
= 37,61. Линейная модель примет вид: Y(t) = (0,81 +37,61)*t
Из этого уравнения находим расчетные
значения Yр(t) и сопоставляем их с фактическими значениями. Такое сопоставление
позволяет оценить приближенные значения коэффициентов сезонности I-IV кварталов F(-3), F(-2), F(-1) и F(0) для года,
предшествующему первому году по которому имеются данные в таблице 1. Эти
значения находим для расчета коэффициентов сезонности первого года F(1), F(2), F(3) и F(4) и других параметров модели Хольта-Уинтерса.
Таблица 2
F(-3)
= [Y
(1)/ Yр(1) + Y (5)/ Yр(5)]/2 = 0,8616;
F(-2)
= [Y
(2)/ Yр(2) + Y (6)/ Yр(6)]/2 = 1,0770;
F(-1)
= [Y
(3)/ Yр(3) + Y (7)/ Yр(7)]/2 = 1,2715;
F(0)
= [Y
(4)/ Yр(4) + Y (8)/ Yр(8)]/2 = 0,7896.
Оценив значения а(0), b(0), а также F(-3), F(-2), F(-1) и F(0), можно перейти к построению
адаптивной мультипликативной модели Хольта-Уинтерса. ()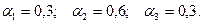
Таблица 3
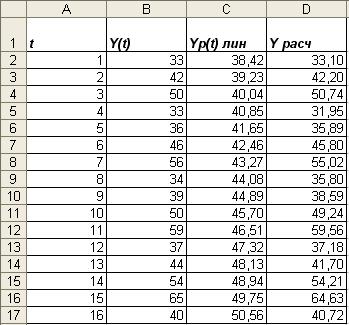
2.
Условие точности выполняется, если относительная
погрешность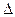 
Y (абсолютное
значение отклонения abs{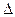Y},
поделенное на фактическое значение Y(t) и выраженное в процентах 100%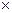 
abs{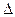Y}/Y(t)) в среднем не превышает 5%.
Таблица 4
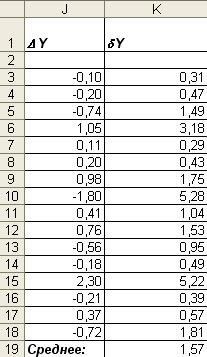
Из таблицы 4 видим, что это значение равно 1,57%. Следовательно,
условие точности выполнено.
3.
Оценка адекватности построенной модели на основе случайности остаточной компоненты по
критерию пиков:
Проверку случайности уровней остаточной компоненты (гр.1 табл.4)
проводим на основе критерия поворотных точек. Для этого каждый уровень ряда
сравниваем с двумя соседними. Если он больше (или меньше) обоих соседних
уровней, то точка считается поворотной (1), в противном случае ставится 0.
Таблица 5
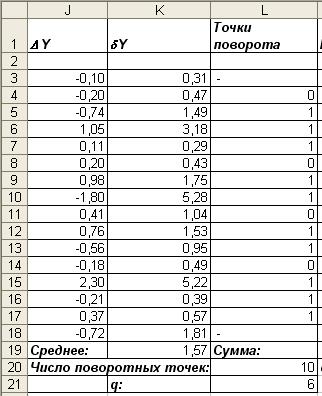
Общее число поворотных точек р=10.
Рассчитаем значение q:
q = int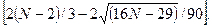
q = int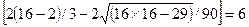
.
Если количество поворотных точек р больше q, то условие случайности уровней
выполнено. В нашем случае р=10, q=6,
значит условие случайности уровней ряда остатков выполнено.
Проверка независимости
уровней ряда остатков по d-критерию (критические
значения d1=1,10
и d2=1,37).
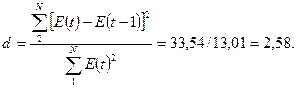
Т.к d
больше 2, значит имеет место отрицательная автокорреляция. В этом случае
величину d уточняют, вычитая полученное значение из 4. получаем d = 1,42. Сравниваем его с
табличными значениями d1
и d2.
Если d2
<d<2, то уровни
ряда остатков независимы. В нашем случае это условие выполнено, так как 1,37<1,42<2.
Проверка независимости
уровней ряда остатков по первому коэффициенту автокорреляции r(1)=0,32:
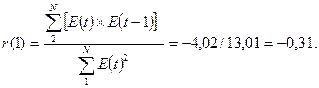
Таблица 6
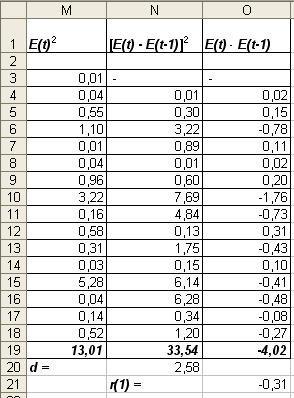
Если модуль рассчитанного значения первого коэффициента автокорреляции
меньше критического, то уровни ряда остатков независимы. Имеем: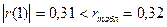 
- значит уровни ряда
независимы.
Проверка соответствия ряда
остатков нормальному распределению по RS-критерию. Рассчитаем
значение RS:
RS =(Emax-Emin)/S,
где Emax –
максимальное значение уровней ряда остатков;
Emin – минимальное значение ряда
остатков;
S – среднее квадратическое отклонение.
Emax = 2,3;
Emin = -1,8, Emax- Emin = 2,3 – (-1,8) = 4,1;
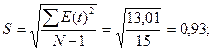
RS =
4,1/0,93 = 4,39.
Так как 3<4,39>4,21, уровни ряда остатков не подчиняются
нормальному распределению.
4.
Рассчитав значения а(16) и b(16) (см.табл.2), можно определить
прогнозные значения показателя Yр(t). Для t = 17 имеем:
Yр(17)
= 
.
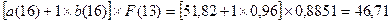Аналогично находим Yр(18), Yр(19) и Yр(20):
Yр(18)
= 
;
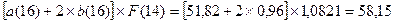Yр(19) =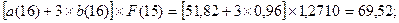 
.
Yр(20)
= 
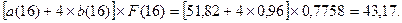
5.
ЗАДАНИЕ
2
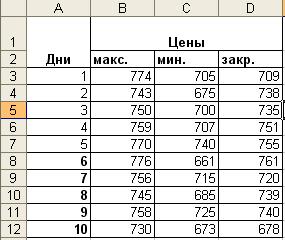
Даны цены (открытия, максимальная, минимальная и закрытия) за 10
дней. Интервал сглаживания принять равным пяти дням. Рассчитать:
-
Экспоненциальную скользящую среднюю;
-
Момент;
-
Скорость изменения цен;
-
Индекс относительной силы;
-
%R,
%K и %D.
Расчеты проводить для всех дней, для которых эти расчеты можно
выполнить на основании имеющихся данных.
Решение:
Экспоненциальная скользящая
средняя (ЕМА).
Рассчитывается по формуле:
EMAt = k Ct + (1-k) EMAt-1 ,
где k = 2/(n+1);
Ct - цена закрытия t-го дня;
EMAt – значение
EMA текущего дня t.
k = 2/(5+1) =
0,333
EMA1 =
709
EMA2 =
0,333*709 + (1-0,333)*709 = 709
EMA3 =
0,333*738 + (1-0,333)*709 = 718,66;
EMA4 =
0,333*735 + (1-0,333)*718,66 = 724,11;
EMA5 =
0,333*751 + (1-0,333)*724,11 = 733,07;
EMA6 =
0,333*755 + (1-0,333)*733,07 = 740,38;
EMA7 =
0,333*761 + (1-0,333)*740,38 = 747,26;
EMA8 =
0,333*720 + (1-0,333)*747,26 = 738,18;
EMA9 =
0,333*739 + (1-0,333)*738,18 = 738,45;
EMA10 = 0,333*740 + (1-0,333)*738,45 = 738,96.
Момент (МОМ)
Момент рассчитывается как разница конечной цены текущего дня Ct и цены n дней тому назад Ct-n
MOMt = Ct
- Ct-n,
MOM6 =
761 – 709 = 52;
MOM7
= 720 – 738 = -18;
MOM8
= 739 – 735 = 4;
MOM9
= 740 – 751 = -11;
MOM10
= 678 – 755 = -77.
Положительные значения MOM свидетельствуют об относительном росте цен, отрицательные – о
снижении.
Скорость изменения цен (ROC). Рассчитывается как отношение конечной цены текущего дня
к цене n дней тому
назад, выраженное в процентах.
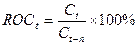
ROC6 =
761/709*100 = 107,33%;
ROC7 =
720/738*100 = 97,56%;
ROC8 =
739/735*100 = 100,54%;
ROC9 =
740/751*100 = 98,54%;
ROC10
= 678/755*100 = 89,8%.
Индекс относительной силы (RSI). Для расчета применяют формулу:
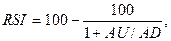
где AU – сумма
приростов конечных цен за n последних дней;
AD – сумма
убыли конечных цен за n последних дней.
AU = (761-755)
+ (739-720) + (740 – 739) = 26
AD = ([720-761]) + ([678 – 740])
= 103
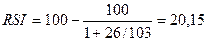- зона перепроданности
Стохастические линии: %К, %D, %R.
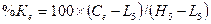, где
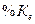- значение индекса
текущего дня t;
Ct – цена
закрытия текущего дня t;
L5
и Н5 – минимальная и максимальная цены за 5 предшествующих дней,
включая текущий.
%К5 = 100*(755-709)/(755-709) = 100;
%К6 = 100*(761-735)/(761-735) = 100;
%К7 = 100*(720-720)/(761-720) = 0
%К8 = 100*(739-720)/(761-720) = 46,34;
%К9 = 100*(740-720)/(761-720) = 48,78;
%К10 = 100*(678-678)/(761-678) = 0.
Индекс %D рассчитывается аналогично индексу %К, с той лишь разницей,
что при его построении величины (Ct – L5)
и (H5 – C5) сглаживают,
беря их трехдневную сумму.
%Dt =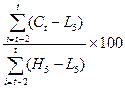 
%D7 =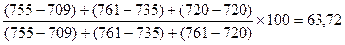 
;
%D8 =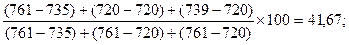 
%D9 =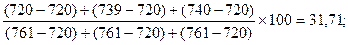 
%D10 =
.
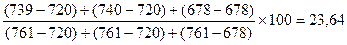%Rt = 100*(H5-Ct)/(H5-L5),
где
%Rt
– значение индекса текущего дня t;
Ct
– цена закрытия текущего дня t;
L5
и Н5 – минимальная и максимальная цены за 5 предшествующих дней,
включая текущий.
%R5 = 100*(755-755)/(755-709)
= 0;
%R6 = 100*(761-761)/(761-735) =
0;
%R7 = 100*(761-720)/(761-720) =
100;
%R8 = 100*(761-739)/(761-720) =
53,66;
%R9 = 100*(761-740)/(761-720) =
51,22;
%R10 = 100*(761-678)/(761-678) =
100.
задание 3
Выполнить различные коммерческие расчеты, используя данные,
приведенные в таблице. В условии задачи значения параметров приведены в виде
переменных. Например, S
означает некую сумму средств в рублях, Тлет – время в годах, i – ставку в процентах и т.д. По именам
переменных из таблицы необходимо выбрать соответствующие численные значения
параметров и выполнить расчеты.
|
Вариант
|
Сумма
|
Дата начальная
|
Дата конечная
|
Время в
днях
|
Время в
годах
|
Ставка
|
Число начислений
|
|
|
Тн
|
Тк
|
Тдн
|
Тлет
|
i
|
m
|
|
4
|
2000000
|
16.01.02
|
14.03.02
|
180
|
4
|
25
|
2
|
3.1 Банк, выдал ссуду,
размером 2000000 руб. Дата выдачи ссуду -16.01.02, возврата – 14.03.02. День
выдачи и день возврата считать за 1 день. Проценты рассчитываются по простой
процентной ставке 25% годовых. Найти:
3.1.1. точные проценты с
точным числом дней ссуды:
к = 365; t
= 57; i = 25%.
I =
2000000*0,25*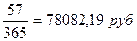
.
3.1.2. обыкновенные
проценты с точным числом дней ссуды:
к = 360; t
= 57; i = 25%.
I =
2000000*0,25*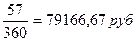
3.1.3. обыкновенные
проценты с приближенным числом дней ссуды:
к = 360; t
= 58; i = 25%.
I =
2000000*0,25*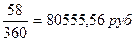
3.2 Через 180 дней после
подписания договора должник уплатит 2000 000 руб. Кредит выдан под 25%
годовых (проценты обыкновенные). Какова первоначальная сумма и дисконт?
S = 200000 руб, i = 0,25; t = 180; к = 360
P = S/(1+ni) = 
= 1777777,78 руб.
D =
2000000 – 1777777,78 = 222222,22 руб.
3.3 Через 180 дней
предприятие должно получить по векселю 2000000 руб. Банк приобрел этот вексель
с дисконтом. Банк учел вексель по учетной ставке 25% годовых (год равен 360
дням) Определить полученную предприятием сумму и дисконт.
S = 200000 руб, i = 0,25; t = 180; к = 360
D = Snd = 2000000*0,25*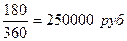
Р = S – D =
2000000 – 250000 = 1750000 руб.
3.4 В кредитном договоре
на сумму 2000000 руб. и сроком на 4 года, зафиксирована ставка сложных
процентов, равная 25% годовых. Определить наращенную сумму.
Р = 2000000 руб.; i
= 0,25; n=4
S =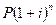 
S =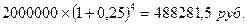 
3.5 Ссуда, размером
2000000 руб. предоставлена на 4 года. Проценты сложные, ставка 25% годовых.
Проценты начисляются 2 раза в год. Вычислить наращенную сумму.
S =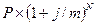 
S =
2000000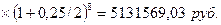
3.6 Вычислить
эффективную ставку процента, если банк начисляет проценты 2 раза в год, исходя
из номинальной ставки 25% годовых.
j = 0,25; m = 2
jэ =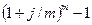 
jэ =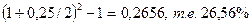 
3.7 Определить какой
должна быть номинальная ставка при начислении процентов 2 раза в год, чтобы
обеспечить эффективную ставку 25% годовых.
jэ = 25%; m = 2
j = m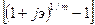
j = 2*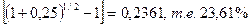
3.8 Через 4 года
предприятию будет выплачена сумма 2000000 руб. Определить ее современную
стоимость при условии, что применяется сложная процентная ставка 25% годовых.
S = 2000000 руб.;
i = =25%; n = 4
P = S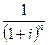
P = 2000000*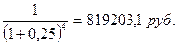
3.9 Через 4 года по
векселю должна быть выплачена сумма 2000000 руб. Банк учел вексель по сложной
учетной ставке 25% годовых. Определить дисконт.
S = 2000000; dсл = 25%
Р = S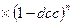
D = S - P
P = 2000000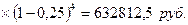
D = 2000000 –
632812,5 = 1367187,5 руб.
3.10 В течение 4 лет на
расчетный счет в конце каждого года поступает по 2000000 руб., на которые 2
раза в год начисляются проценты по сложной годовой ставке 25%. определить сумму
на р/с к концу указанного срока.
R = 2000000; n =
4; i = 25%
S =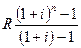 
S = 2000000