Введение.

Устойчивость или неустойчивость линейной стационарной системы определяется расположенным на S-плоскости нулей ее характеристического уравнения. Устойчивость системы не зависит от начальных условий или ее входных сигналов. Для нелинейных систем это перестает быть справедливым.

Ограниченность или неограниченность реакции нелинейной системы может зависеть от начальных условий или вынуждающей функции.

Устойчивость в смысле Ляпунова.

Под устойчивостью систем автоматического регулирования обычно понимают свойство системы возвращаться к первоначальному состоянию после прекращения действия внешнего возмущения.

            Требование устойчивости определяет, как правило, работоспособность системы. Полагая, что система автоматического регулирования описывается системой обыкновенных дифференциальных уравнений. Рассмотрим устойчивость решений дифференциальных уравнений. Пусть поведение системы автоматического регулирования описывается системой обыкновенных дифференциальных уравнений:

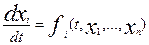 (i =1, 2, 3,…, n),  (1)

где x_i – переменные, характеризующие состояния системы.

            В векторной форме систему (1) можно записать следующим образом:

  (2)

            В уравнении (2) принято обозначение:

, , .

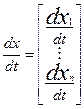Если система (1) является автономной (если вектор-функция f не зависит явно от времени t, т.е. система дифференциальных уравнений имеет в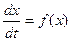ид , то система уравнений называется автономной (стационарной)), то уравнение (2) имеет вид:

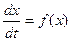.  (3)

            Введем в рассмотренные (n + 1)-мерное пространство Eⁿ⁺¹, координатами которого являются t, x₁,…, x_n. Будем рассматривать только такие системы, правые части которых по всем аргументам и имеют непрерывные частные производные по независимым переменным x₁,…, x_n в некоторой выпуклой области g пространства Eⁿ⁺¹. В этом случае выполняются условия теоремы существования и единственности, т.е. для любых начальных значений t₀, x₁₀,…, x_n0 существует, и притом единственное решение:

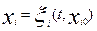(i =1, 2, 3,…, n),  (4)

удовлетворяющее начальным условиям:

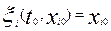(i =1, 2, 3,…, n).  (5)

Будем считать функции ξ_i(t) оптимальными для t₀ < t < ∞,

причем t₀ можно считать равным - ∞.

            Рассмотрим некоторое решение системы (2) 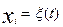, определенное на интервале [t₀, ∞), причем .

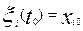            Решение ξ_i(t) называется устойчивым по Ляпунову при t → ∞, если для любого ε>0 существует такое δ>0, зависящее от ε и t, что любое решение x_i = φ_i(t), для которого t = t₀ выполняется неравенство │φ_i(t₀) - ξ_i(t₀)│< δ, удовлетворяет неравенству │φ_i(t) - ξ_i(t)│< ε, при t₀ ≤ t < ∞ для всех i =1, 2, 3,…, n.

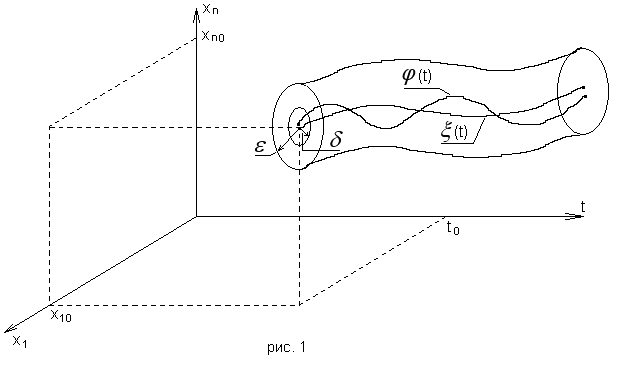
            Геометрически это означает, что все решения, которые при t = t₀ начинается в δ-окрестности точки(x₁₀,…, x_n0), никогда не покинут ε-трубку решение ξ(t) (рис.1).

            Решение ξ₁(t) называется неустойчивым, если существует ε>0 такое, что для любого δ>0 найдется такой момент времени t = t₁, что для некоторого значения i = k и t = t₁ будет выполняться неравенство: │φ_k(t₁) – ξ_k(t₁)│≥ ε, несмотря на то что: │φ_k(t₀) – ξ_k(t₀)│< δ для всех i =1, 2, 3,…, n.

            Решение ξ_i(t) называется ассиметрически устойчивым, если:

1)     Решение ξ(t) устойчиво по Ляпунову при t → ∞;

2)     Существует такое число μ > 0, что для любого решения φ_i(t), удовлетворяющие при t = t₀ неравенство:

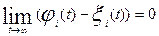
            Если μ = ∞, то динамическая система называется устойчивой в целом.

Устойчивость однородной системы.

Рассмотрим линейную систему дифференциальных уравнений:

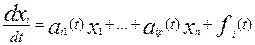,  (6)

где a_ij(t), f_i(t) – непрерывные функции на полуинтервале [b ≤ t ≤ ∞).

В векторной форме систему (6) можно представить следующим образом:

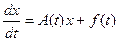,  (7)

где:

, , .

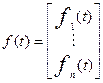            Однородная система, соответствующая (7), имеет вид: 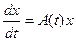  (8).

            Эта система имеет тривиальное решение x(t)≡0.

            Устойчивость произвольного решения связывают с устойчивостью тривиального решения.

Теорема 1: Любое решение однородной системы линейных дифференциальных уравнений устойчиво тогда и только тогда, когда устойчиво ее тривиальное решение

            Доказательство:

            Докажем, сначала достаточность условия теоремы. Пусть тривиальное решение x(t)≡0 устойчиво. Это означает, что для любого ε>0 существует δ>0 такое, что для любого решения х = ξ(t), удовлетворяющего при t = t₀ неравенству ║ξ(t₀)║< δ, будет справедливо неравенство ║ξ(t)║< ε для всех значений t ≥ t₀.

            Пусть x = ψ(t) – произвольное решение. Докажем его устойчивость. Обозначим через x = φ(t) другое произвольное решение, удовлетворяющее при t = t₀ условию:

║ψ(t₀) - φ(t₀)║ < δ.  (9)

            Из свойств однородной системы следует, что разность ψ(t) - φ(t) = ξ(t) – также решение системы (8), причем в силу устойчивости тривиального решения получим неравенство ║ψ(t) - φ(t)║ < ε при t = t₀, что означает устойчивость решения x = ψ(t). Достаточность доказана.

            Выполним доказательство необходимости условия теоремы. Пусть решение x=ψ(t) устойчиво. Покажем, что тогда будет устойчиво тривиальное решение. Устойчивость решения означает, что для произвольного решения φ(t), удовлетворяющего при t = t₀ неравенству ║ψ(t₀) - φ(t₀)║ < δ, будет справедливо неравенство ║ψ(t) - φ(t)║ < ε при t ≥ t₀.

            Пусть х = ξ(t) – решение системы (8), удовлетворяющее условию ║ξ(t₀)║< δ. Запишем это решение в виде: ξ(t) = [ξ(t) + ψ(t)] - ψ(t). Сумма решений ξ(t) + ψ(t) представляет собой также решение системы (8), причем при t = t₀ справедливо неравенство

║[ξ(t) + ψ(t)] - ψ(t)║ < δ. Тогда из устойчивости решения ψ(t) следует, что при t > t₀ будет выполняться неравенство:

║[ξ(t) + ψ(t)] - ψ(t)║ = ║ξ(t₀)║< ε,  (10)

что и означает устойчивость тривиального решения. Этим доказана необходимость условия теоремы.

            Из теоремы следует, что в линейной однородной системе с нетривиальными коэффициентами из устойчивости хотя бы одного решения вытекает устойчивость всех остальных решений, и обратно, из неустойчивости одного решения вытекает неустойчивость всех остальных решений.

            Однородная линейная система дифференциальных уравнений, все решения которой устойчивы, называется устойчивой системой, если все решения этой системы неустойчивы, то неустойчивая система.

Теорема 2: Линейная однородная система дифференциальных уравнений (ЛОСДУ) устойчива тогда и только тогда, когда каждое решение ограничено для t ≥ t₀.

            ЛОСДУ называется асимптотически устойчивой, если каждое ее решение асимптотически устойчиво.

Теорема 3: ЛОСДУ устойчива тогда и только тогда, когда асимптотически устойчиво ее тривиальное решение.

Из теоремы следует:

1)         Асимптотически устойчивая линейная однородная система устойчива в целом;

2)         Если в линейной однородной системе асимптотически устойчиво хотя бы одно решение, то все остальные решения так же асимптотически устойчивы.

Устойчивость неоднородной системы.

Теорема 4: Линейная неоднородная система дифференциальных уравнений (ЛНСДУ) устойчива (асимптотически устойчива) тогда и только тогда, когда устойчива (асимптотически устойчива) соответствующая однородная система уравнений.

            Доказательство:

            Пусть однородная система (8) устойчива. Покажем, что в этом случае будет устойчива и неоднородная система (7), т.е. будет устойчиво любое ее решение.

            Пусть x=ψ(t) – некоторое решение системы (2). Исследуем на устойчивость. Рассмотрим норму разности ║ψ(t) - φ(t)║, где φ(t) – некоторое другое решение системы (2) с начальным условием φ(t₀), удовлетворяющим неравенству:

║ψ(t₀) - φ(t₀)║ < δ.  (11)

            Разность двух решений ψ(t) - φ(t) неоднородной системы (7) является решением однородной системы (8). По условию теоремы однородная система (8) устойчива, т.е. выполнено неравенство (11), то для всех t ≥ t₀ справедливо неравенство ║ψ(t) - φ(t)║ < ε, что и означает устойчивость решения x=ψ(t) неоднородной системы.

Критерий Гурвица.

Рассмотрим полином:

P(λ) = a₀ λⁿ + a₁ λ^n-1 +…+a_n (n ≥ 1)  (12)

Будем полагать, что a_i – действительные числа, получим a₀>0. В общем случае корни полинома P(λ) могут быть комплексными числами и полином P(λ) может рассматриваться как функция комплексного переменного λ = a + iβ. Такой полином называется стандартным.

            Стандартным полиномом называется полиномом Гурвица или Гурвицевым полиномом, если действительные части всех корней отрицательны, т.е. все корни расположены в левой полуплоскости:

Re λ_i < 0 (i = 1, 2,…, n).  (13)

Теорема 5: Если стандартный полином есть полином Гурвица, то все его корни положительны.

            Доказательство:

            Пусть полином (12) имеет комплексные корни λ_m = -a_m + iβ_m (m = 1, 2,…, μ, a_m>0), причем их кратности соответственно равны е₁, е₂,…, е_μ. Но для полинома с действительными коэффициентами каждому комплексному корню соответствует сопряженный корень, причем той же кратности. Таким образом, число 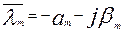 так же  будут корнями полинома P(λ) с кратностями е₁, е₂,…, е_μ.

            Пусть действительные корни полинома будут λ_n = -Y_n (n = 1, 2,…,υ), Y_n >0 и их кратности соответственно равны е_n. Тогда полином P(λ) можно разложить на линейные множители, т.е. записать в виде:

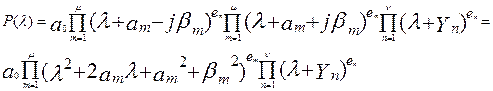
            Из разложения следует, что коэффициенты a_i полинома P(λ) положительны.

            Для полинома первой и второй степени необходимое условие является также достаточным.

            Для полинома третьей и выше степени это условие достаточным не будет.

            Пусть имеется стандартный полином Гурвица P(λ) = a₀ λⁿ + a₁ λ^n-1 +…+a_n.

Построим полином P^*(λ) следующим образом:

P^*(λ) = (-1)ⁿP(-λ) = a₀ λⁿ - a₁ λ^n-1 +…+(-1)ⁿ a_n.  (14)

Все корни полинома P(λ) расположены в левой полуплоскости, поэтому полином P^*(λ) имеет все корни в правой полуплоскости.

            Пусть с > 0 – некоторое положительное число.

            Полином: Q(λ) = (λ + c)P(λ) + λP^*(λ)  (15) называется полиномом, присоединенным к полиному P(λ). Степень полинома Q(λ) на единицу выше, чем степень P(λ).

Лемма 1:

            Для каждого полинома Гурвица его присоединенные полиномы так же являются стандартными полиномами Гурвица.

Лемма 2:

            Каждый стандартный полином Гурвица степени выше первой является присоединенным для некоторого стандартного полинома Гурвица более низкой степени.

            Если полином Q(λ) = A₀ λⁿ⁺¹ - A₁ λⁿ +…+ A_n+1 – стандартный полином Гурвица степени n + 1, то стандартный полином Гурвица P(λ) степени n, для которого полином Q(λ) является присоединенным, определяется выражением:

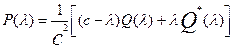,  (16)

где .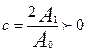

            Из лемм следует, что для любого стандартного полинома Гурвица P(λ) степени n можно построить как стандартный полином Гурвица Q(λ) степени n + 1, который будет присоединенный к полиному P(λ), так и стандартный полином Гурвица R(λ) степени n+1, для которого полином P(λ) будет присоединенным.

            Построим пространство полиномов Гурвица μ = {P(λ)}. Это пространство представляет собой объединение пространств μ_n, соответствующих полиномам Гурвица различных степеней.

            Согласно леммам, если полином P(λ)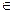μ_n, то присоединенный к нему полином Q(λ)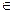μ_n+1, и обратно, существует такой полином R(λ)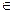μ_n-1, для которого полином P(λ)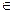μ_n является присоединенным.

            Пусть P(λ) = a₀ λⁿ + a₁ λ^n-1 +…+a_n – некоторый многочлен, причем a_i – действительные коэффициенты и a₀>0 образуют матрицу размера n×n

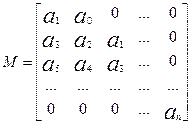  (17)

            Эта матрица строится следующим образом: по главной диагонали откладываются a_1,…,a_n. В право по строке от этих коэффициентов расположены коэффициенты с убывающими номерами, влево - с возрастающими.

            При этом полагается a_i =0, если i<0 или i>n. Такая матрица М называется матрицей Гурвица. Главные диагональные миноры будут иметь вид:

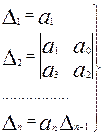  (18)

Теорема 6: Для того, чтобы стандартный полином P(λ) был полиномом Гурвица, необходимо и достаточно, чтобы все главные диагональные миноры его матрицы Гурвица были положительны, т.е. Δ_k > 0 (k = 1, 2,…, n). (19)

            Условие (19) называется условием Гурвица.

Второй метод Ляпунова.

Второй, или прямой, метод Ляпунова позволит исследовать устойчивость решений нелинейных дифференциальных уравнений, не производя решение самих уравнений

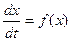,  (20)

где: , 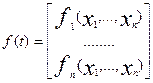.  (21)

            При этом полагаем, что функции f_i(x₁,…, x_n) имеют непрерывные частные производные по всем аргументам в некоторой выразимой области ς: ║х║≤μ n-мерного пространства.

1)     Законоопределенные и законопостоянные функции.

Рассмотрим функции V(x₁,…, x_n) определенные и непрерывные в области ς:║х║≤μ и обладающими в этой области непрерывными частными производными по переменным x₁,…, x_n.

Функция V(x) называется знакоположительной (знакоотрицательной) в указанной области ς, если для любого x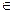ς имеем V(x)≥0 (V(x)<0), причем V(x)=0 тогда и только тогда, когда x =0.

Функции V(x) первого типа называются знокопостоянными, второго - знакоопределенными.

Пусть функция V(x) является квадратичной формой, т.е. 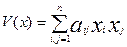.  (22)

Функция V(x) является определенно положительной (определенно отрицательной), если положительно определена (отрицательно определена) квадратичная форма (22). Квадратичная форма является положительно определенной тогда и только тогда, когда все главные диагональные миноры ее матрицы строго положительны.

Дадим знакоположительной функции V(x) геометрическую интерпретацию. Для простоты рассмотрим функцию двух переменных V(x₁, x₂). На плоскости x₁x₂ линия V(x₁, x₂)=с, где с – некоторое число, представляющее собой правило, содержащую внутри начало координат (рис.2).

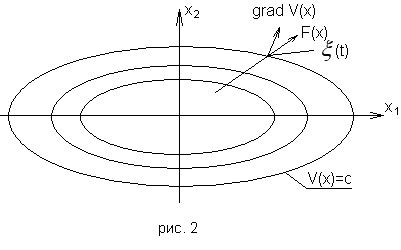
            Пусть ξ(t) – некоторое решение системы (20), удовлетворяющее начальному условию ξ(t₀)=x.

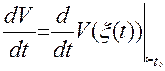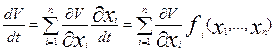            Полной производной по времени t функции V(x) в силу системы (1) называется функция , или   (23)

            Из формулы (4) следует, что производная 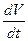 в силу системы (20) не зависит от выбранного решения ξ(t), а является функцией точки x.

            Если ввести обозначения 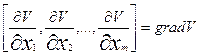, то выражение (23) можно переписать в виде 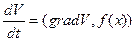.  (24)

            Производная 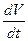 в силу системы (20) представляет собой скалярное произведение вектора gradV на вектор фазовой скорости f(x).

            Положительно определенные функции V(x), производные которых в силу системы (20) являются отрицательно определенным или знакоотрицательными называются функциями Ляпунова.

2)     Теорема Ляпунова об устойчивости.

Теорема 7: Если для системы уравнений (20) существует положительно определенная функция V(x), производная которой в силу системы (20) знакоотрицательна, то тривиальное решение системы x(t)≡0 системы (20) устойчиво по Ляпунову.

            Доказательство:

            Возьмем произвольное число ε >0 и рассмотрим множество значений х, удовлетворяющих соотношению: ║х║= ε.

            Обозначим: 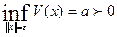  (25)

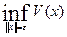 - точная нижняя грань функции V(x) по всем х, удовлетворяющих ║х║= ε.

            Т.к. V(0)=0, то можно указать такую δ-окрестность начала координат в n-мерном пространстве x₁,…, x_n, что V(x)<α, если ║х║< δ.  (26)

            Рассмотрим некоторое решение ξ(t) системы (20), удовлетворяющее начальному условию: ║ξ(t₀)║< δ. Функция V(ξ(t)) будет невозрастающей функцией t вдоль этого решения, т.к. производная в силу любых t > t₀ выполняется неравенство:

V(ξ(t)) ≤ V(ξ(t₀)) < α.  (27)

            Покажем, что для любых t > t₀ справедливо неравенство: ║ξ(t)║< ε.  (28)

            Пусть для некоторого момента времени t₁ > t₀ выполняется равенство ║ξ(t₁)║= ε₁, тогда 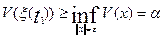.  (29)

            Это противоречит неравенству (27).

            Из доказательства теоремы следует способ определения по заданному t >0 такого числа δ >0, что ║ξ(t)║< ε, если при t₁ = t₀ справедливо неравенство ║ξ(t₀)║< δ. Для этого по заданному числу ε >0определяют 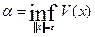, а затем выбирают δ >0 так, чтобы V(ξ(t₀)) < α для всех ξ(t₀) удовлетворяющих условию ║ξ(t₀)║< δ.

3)     Теорема Ляпунова об асимптотической устойчивости.

Теорема 8: Пусть для системы дифференциальных уравнений (1) существует положительно определенная функция V(x), производная которой в силу системы (20) отрицательно определена. Тогда тривиальное решение x(t)≡0 системы (20) асимптотически устойчиво по Ляпунову.

            Доказательство:

            Асимптотическая устойчивость тривиального решения означает, что:

1)     тривиальное решение x(t)≡0 устойчиво;

2)     если в начальный момент времени t₀ некоторое решение ξ(t) удовлетворяет неравенству ║ξ(t₀)║<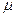, то .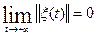

Устойчивость тривиального решения следует из предыдущей теоремы.

Рассмотрим произвольное нетривиальное решение ξ(t) системы (20), удовлетворяющее при t₁ = t₀ неравенству ║ξ(t₀)║<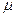, и покажем, что.

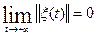Получим поведение функции V(x) вдоль этого решения. Т.к. производная функции V(x) в силу системы (20) 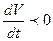, то функция V(x) моментально убывает вдоль решения ξ(t) при возрастании t. Эта функция ограничена снизу, т.к. V(x)≥0. Всякая монотонно убывающая, ограниченная снизу функция имеет предел, следовательно существует предел: 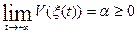.  (30)

Пусть α>0, тогда ║ξ(t)║≥ β >0, для всех t₁ ≥ t₀.

Если бы существовала последовательность значений {t_k}→ + ∞ такая, что (║ξ(t_k)║≥β>0 для всех t₁ ≥ t₀ при k→ ∞).

║ξ(t_k)║ → 0 при k→ ∞, то V(ξ(t_k)) → 0 при k→ ∞. Это противоречит утверждению, что α>0.

В силу отрицательность определенности производной 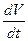 из уравнения ║ξ(t)║≥β>0 следует, что 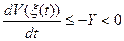,  (31)

где Y>0 – некоторое действительное число, тогда

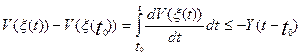.  (32)

            Из интеграла (32) получим:

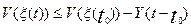.  (33)

            При достаточно большом t будет справедливо неравенство (ξ(t))<0, что противоречит условию положительной определенности функции V(x).

            Следовательно: 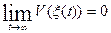.  (34)

            Докажем, что 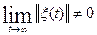. Пусть существует последовательность {t_k}→ ∞ такая, что .

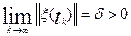            Тогда 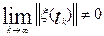, что противоречит равенству (34). Следовательно ║ξ(t)║ → 0 при t = t₀.

4)     Теорема Ляпунова о неустойчивости.

Теорема 9: Если для системы уравнений (20) существует непрерывная функция V(x), удовлетворяющая условию V(0)=0, производная которой в силу системы (20) знакоопределенная, причем в любой окрестности начала координат имеются точки, в которых знак функции V(x) совпадает со знаком ее производной, то тривиальное решение неустойчиво в смысле Ляпунова.

            Доказательство:

            Пусть множество точек х, удовлетворяющих неравенству ║х║<μ, является областью знакоопределенной производной 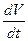функции V(x) в силу системы (20). Покажем, что как бы ни было мало число δ >0. В этом случае всегда имеется решение ξ(t) системы (20), обладающее следующими свойством:

Найдется такой момент времени t, при котором будет справедливо неравенство ║ξ(t₁)║≥ ε, несмотря на то, что в начальный момент времени t = t₀ выполнялось неравенство ║ξ(t₀)║< δ. Это и будет означать неустойчивость тривиального решения.

            Выберем ε = μ. Для определенности наложим 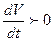. Выберем начальную точку ξ(t₀) так, чтобы V(ξ(t₀))> 0. По условию задачи такой выбор ξ(t₀) всегда возможен. Рассмотрим теперь решение ξ(t), удовлетворяющее начальному условию. Т.к. производная 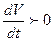 вдоль решения ξ(t), то функция V(ξ(t)) возрастает вдоль этого решения. Следовательно: V(ξ(t)) ≥ V(ξ(t₀)) при t > t₀.  (35)

            Из неравенства (35) получим, что решение ξ(t) не приближается к началу координат, т.е. ║ξ(t)║≥ α >0,  (36)

т.к. 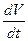 - определенно положительная функция, то в области α ≤║х║≤ μ производная 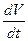 удовлетворяет неравенству: .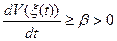

            Покажем, что найдется такой момент времени t₁, для которого ║ξ(t₁)║≥ μ. Действительно, пусть для всех значений t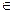[t₀, ∞) справедливо неравенство ║ξ(t)║< μ, но

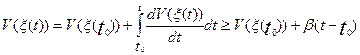.  (37)

            Из формулы (37) следует, что функция V(ξ(t)) неограниченно возрастает при t→ ∞. Получим противоречие, т.к. из неравенства ║ξ(t)║< μ следует ограниченность V(ξ(t)) для любых t.

Исследование устойчивости по уравнениям первого приближения.

1)     Уравнения первого приближения.

Пусть поведение системы автоматического регулирования описывается системой дифференциальных уравнений: 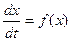.  (38)

Пусть, кроме того, f(0)=0, т.е. начало координат х = 0 является состоянием равновесия. Исследование устойчивости любого состояния равновесия можно свести к этому случаю с помощью соответствующей замены переменных.

Будем полагать, что функции f_i(x₁,…, x_n) имеют непрерывные частные производные в некоторой области ║х║<μ. Разложим функции f_i(x₁,…, x_n), являющиеся компонентами вектор-функции f(x), в ряд Тейлора в окрестности начала координат:

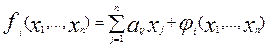; (i = 1, 2,…, n),  (39)

где 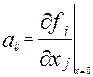, функции  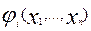содержат члены разложения порядка малости выше первого относительно переменных x₁,…, x_n и поэтому:

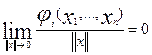.  (40)

            С учетом равенства (39) систему (38) можно переписать в виде: 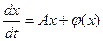,(41)

где А= [a_ij] – числовая матрица А;

      φ(х) – вектор столбец, удовлетворяющий условию: 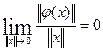.  (42)

            СЛДУ с постоянными коэффициентами: 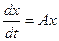  (43) называется системой первого приближения для (41), а значит и для системы (38).

2)     Теорема Ляпунова об устойчивости в первом приближении.

Теорема 10: Тривиальное решение системы (41) автоматически устойчиво по Ляпунову, если все корни характеристического уравнения матрицы А системы (41) имеют отрицательные вещественные части, т.е. Re λ_i < 0 (i = 1, 2,…, n).

Теорема 11: Если среди корней характеристического уравнения матрицы А хотя бы один корень с положительной вещественной частью, то тривиальное решение системы (41) неустойчиво.

Исследование устойчивости нелинейных систем автоматического регулирования с помощью второго метода Ляпунова.

1)     Уравнение нелинейных систем. Состояние равновесия.

Пусть нелинейная система автоматического регулирования состоит из линейного объекта регулирования и нелинейного регулятора. Поведение объекта регулирования описывается линейной системой дифференциальных уравнений с постоянными коэффициентами, которая в векторной записи имеет вид: 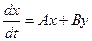,  (44) где  - вектор координат, характеризующих состояние объекта регулирования; у – скалярная координата, характеризующая воздействие регулятора на объект регулирования. Матрица А полагается невырожденной (detA≠0). Регулятор в своем составе имеет сервомеханизм, уравнение которого:

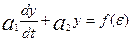  (45)

и чувствительный элемент, формирующий минор ошибки: ε = c^тх – rу,  (46) где c^т=[c₁,..,c_n] – векторы постоянных коэффициентов; r – постоянный параметр обратной связи.

            Относительно линейной функции f(ε) будем полагать f(0)=0, εf(ε)>0, если ε≠0.

            Функция f(ε) предполагается непрерывной при ε≠0, а в точке ε = 0 допускается разрыв непрерывности первого рода.

            Система автоматического регулирования будет:

1-     Собственно устойчива, если все корни характеристического уравнения out(A – λE) =0 имеют отрицательные вещественные части Re λ_i < 0.

2-     Нейтральна по координатам x₁,…, x_n, если Re λ₁ = Re λ₂ =…= Re λ_n = 0, а остальные корни характеристического уравнения существуют отрицательные вещественные части.

3-     Собственно неустойчива, если хотя бы один корень характеристического уравнения имеет положительную вещественную часть.

2)     Приведение уравнений движений к канонической форме.

Исследование устойчивости тривиального решения системы:

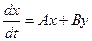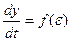; ; ε = c^тх – rу,  (47)

удобно проводить, когда (47) приведена к каноническому виду. Канонической формой уравнений (47) назовем такой их вид, когда матрица А приведена к жордановой форме.

            Сделаем в системе (47) замену переменных:

x = Tu (Dec T≠0).  (48)

            Тогда система уравнений примет вид:

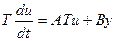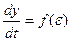; ; ε = c^т Tu – rу,

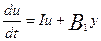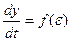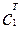или: ; ; ε =  u – rу,  (49)

где В₁=Т^-1В; 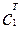=c^т T.

            Система (49) укрощается если выполнить еще раз замену:

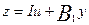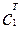, ε =  u – rу.  (50)

            Тогда вместо системы (47) получим систему:

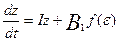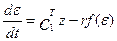, .  (51)

            Система уравнений (51) является канонической формой уравнений движения.

3)     Достаточные условия устойчивости состояния равновесия.

Исследуем устойчивость тривиального решения уравнения (51). Построим функцию Ляпунова, с помощью которой найдем условия накладываемые на параметры регулятора, при вынесении которых тривиальное решение (51) асимптотически устойчиво.

            Рассмотрим случай, когда все корни характеристического уравнения простые и лежат в левой полуплоскости. Функцию Ляпунова будем искать в виде:

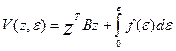.  (52)

            Функция , определяемая выражением (52) будет определенно положительной, если квадратичная форма  - положительно определена.

            Составим полную производную от функции :

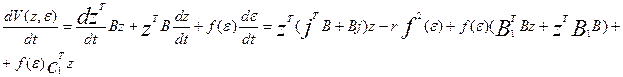
            Учитывая, что матрица квадратичной формы является асимметрической В^т = В получим:

.

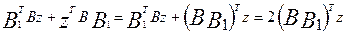            Введем в рассмотрение матрицу

с= -(j^TB + B_j).  (53)

Т.о. полная производная функции  может быть записана в виде:

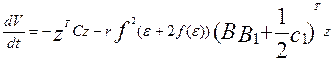.  (54)

            Если характеристические числа матрицы А заданной симметрической матрице С однозначно определяется симметрическая матрица В. Т.к. I=diag μ, то соотношение (53) можно представить в виде: c_ij = -(λ_iB_ij + λ_jB_ij)

откуда: 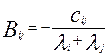.  (55)

Теорема 12: Пусть матрица А устойчива, т.е. ее характеристические числа лежат в левой полуплоскости. Тогда, если с-матрица некоторой положительно определенной квадратичной формы, то определенная по формуле (55) матрица В также является матрицей положительно определенной квадратичной формы.

Список литературы.

•           Чемоданов Б.К., «Математические основы теории автоматического регулирования», 1977

•           Воронов А.А., «Введение в динамику сложных систем», 1980

•           Заде Л., Дезоер Ч., «Теория линейных систем», 1970