Содержание:

Понятие дифференциального уравнения. 3

Представление непрерывных систем в виде дифференциальных уравнений. 3

Преобразование системы дифференциальных уравнений. 4

Основные свойства линейных дифференциальных уравнений. 6

Решение дифференциальных уравнений первого порядка. 6

Общее решение линейной однородной системы. 7

Физический смысл частного и вспомогательного решений. 7

Линейная неоднородная система. Метод вариации произвольных постоянных. 8

Дифференциальные уравнения систем автоматического регулирования. 10

Методика составления дифференциальных уравнений систем автоматического регулирования. 10

Общие замечания. 10

Составление и линеаризация дифференциальных уравнений элементов систем. 10

Понятие пространства состояний. 12

Понятие управляемости и наблюдаемости. 12

Соотношения вход – состояние – выход. 14

Уравнения состояния. 15

Классическим методом описания линейной системы считается записанная при помощи дифференциального или разностного уравнения связь между ее входом и выходом. Дифференциальное уравнение применяется для описания непрерывных систем, а уравнение в конечных разностях — для дискретных систем.

Понятие дифференциального уравнения

Уравнения, которые, кроме неизвестных функций одного или нескольких переменных, содержат также их производные, называются дифференциальными. Дифференциальные уравнения называются обыкновенными, если неизвестные функции являются функциями одного переменного, в противном случае дифференциальные уравнения называются уравнениями в частных производных.

Соотношение вида

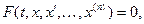
называется дифференциальным уравнением n-го порядка. Решением дифференциального уравнения называется функция x=x(t), определенная на некотором интервале D't, которая, будучи подставлена в это уравнение, обращает его в тождество на всем интервале D. Это уравнение можно рассматривать как функцию, определяющую неявно производную n-го порядка x⁽ⁿ⁾. При определенных условиях его можно решить относительно x⁽ⁿ⁾:

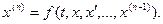
Пусть x=x(t) – решение данного дифференциального уравнения. Тогда x(t) является непрерывной и непрерывно дифференцируемой функцией t. На плоскости (t,x) решению x=x(t) будет соответствовать непрерывная кривая, называемая интегральной кривой.

Функция x=x(t,C) называется общим решением дифференциального уравнения, если путем соответствующего выбора постоянной можно любую интегральную кривую.

Представление непрерывных систем в виде дифференциальных уравнений.

Непрерывную систему часто описывают дифференциальным уравнением относи­тельно ее выхода y(t) и входа r(t). В общем виде уравнение представляется так:

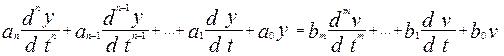(1)

Предполагая, что входной сигнал v (t) известен, правую часть уравнения можно представить как F(t), назы­ваемую часто вы­нуждающей функцией,

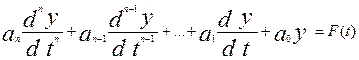 (2)

Для линейных систем а_i и b_i не являются функциями v или у но могут зависеть от вре­мени t.

Для линейных систем с постоянными параметрами эти коэффициенты должны быть постоянными.

Дифференциальное уравнение системы может быть задано или должно быть найдено на основе модели системы, в последнем случае модель дает непосредственно систему дифференциальных уравнений.

Оператор р, обозначающий часто операцию дифференцирования, определяется как

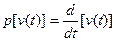 (3)

Если c₁ и c₂ - постоянные величины, то

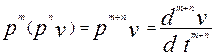    (4),

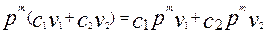   (5),

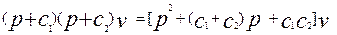  (6), где n и m неотрицательные целые числа. Как правило, с оператором р можно опе­рировать как с алгебраическим числом. Существенным исключением является то, что он в общем случае некоммутативен с функциями

p(tv)≠t(pv)

p(v₁v₂)≠v₁(pv₂).

При помощи оператора р уравнения (1) и (2) приводятся к виду

(a_npⁿ + a_n-1p^n-1 +…+ a₁p + a₀)y(t) = b_mp^m +…+ b₁p + b₀)v(t) = F(t)   (7)

стоящие в скобках перед у и v элементы сами являются операторами.

Для стационарных систем, коэффициенты которых постоянны, последнее выражение записывается символически как

A(p)y(t) = B(p)v(t) = F(t).

Для линейных систем с переменными параметрами, коэффициенты которых являются функциями времени, А и В - зависящие от времени

операторы. Это учитывается выражением

A(p, t)y(t) = B(p, t)v(t) = F(t).

Формальное определение операторов А и В следует из сравнения

последних трех выражений.

Преобразование системы дифференциальных уравнений.

Непрерывная модель может быть описана математически системой дифференциальных уравнений. Один класс уравнений служит главным образом для характеристики отдельных составляющих, а другой - для описания связей между этими составляющими. При математическом описании мо­дели указанные два типа уравнений обычно сочетаются с эксперименталь­ной проверкой. Полученная система уравнений может быть затем сведена к одному уравнению, связывающему вход и выход системы, хотя подобное преобразование не всегда элементарно. Решение системы уравнений с по­стоянными коэффициентами гораздо проще чем системы уравнений с пере­менными коэффициентами, а потому рассматривается в первую очередь.

Пример: Дли цепи изображенной на рисунке запишем уравнение, связы­вающее напряжение на выходе е₂ с напряжением источника e₁. Суммируя токи, выходящие соответственно из узлов 3 и 2, получим

.

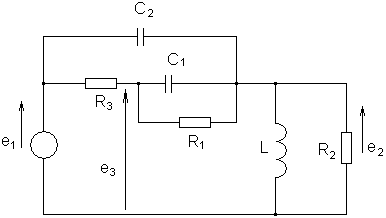
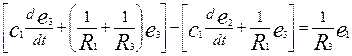
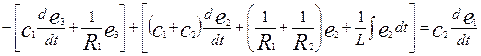Дифференцируя второе уравнение, чтобы избавиться от интеграла, и вводя оператор р - d/dt, приводим уравнения к виду

(p+2)e₃ – (p+1)e₂ = e₁,

-(p²+p)e₃ + (2p²+2p+1)e₂ = p²e₁.

Предполагается, для простоты, что все сопротивления, емкости и индуктив­ности равны соответственно 1 ом, 1 фарада, 1 генри. Помножим каж­дый из членов первого уравнения на оператор р²+р, а каждый из членов второго уравнения - на р + 2 и сложим затем эти уравнения. Поскольку

(p²+p)(p+2)e₃ = (p+2)(p²+p)e₃,

то выражение, содержащее е₃ уничтожится. Тогда

(p+2)(2p²+2p+1)e² – (p²+p)(p+1)e₂ = [(p²+p) + p²(p+2)]e₁

или

(p³ + 4p² + 4p + 2)e₂=(p³ + 3p² + p)e₁, что и является искомым результатом.

Процедура, используемая в данном примере, справедлива для любых двух дифференциальных уравнений с постоянными коэффициентами. Если L озна­чает оператор, являющийся функцией только р, то уравнения можно символиче­ски записать как

L₁₁(p)y₁(t) + L₁₂(p)y₂(t) = F₁(t),

L₂₁(p)y₁(t) + L₂₂(p)y₂(t) = F₂(t).  (8)

Умножим первое уравнение на L₂₁, а второе на L₁₁ и вычтем одно из другого. Так как L₂₁L₁₁y₁=L₁₁L₂₁y₁, то

(L₁₁ L₂₂ – L₂₁ L₁₂)y₂ = L₂₁F₁ + L₁₁F₂   (9)

Аналогично,

(L₁₁ L₂₂ – L₂₁ L₁₂)y₁ = L₂₂F₁ + L₁₂F₂   (10)

Каждое из последних двух уравнений содержит лишь одну не­зависимую пе­ременную.

Изложенный материал ограничивался дифференциальными уравнениями с постоянными коэффициентами. Получение дифференциального уравнения, связывающего вход и выход, для систем с переменными коэффициентами гораздо сложнее. Пред­положим, что система описывается уравнениями

t(py₁) + p(t²y₂) = F₁(t),

p(ty₁) + t(py₂) = F₂(t).

Чтобы исключить у₁, из этих уравнений, можно попытаться умножить первое из них на pt, а второе на tp и затем вычесть одно из другого. Если это выполнено, то

pt²(py₁) + pt(pt²y₂) = ptF₁(t),

tp(pty₁) + tp(tpy₂) = tpF₂(t).

Однако pt²(py₁) = (t²p² + 2tp)y₁, а tp(pty₁) = t(tp² + 2p) y₁. Следовательно, исключить у₁ вычитанием нельзя.

Для систем с переменными параметрами уравнения (9) и (10) несправедливы, так как

Основные свойства линейных дифференциальных уравнений.

Линейное дифференциальное уравнение n-го порядка можно записать в форме:

(a_npⁿ + a_n-1p^n-1 +…+ a₁p + a₀)y(t) = F(t).  (11)

В связи с тем, что все выражения справедливы как для систем с постоянными, так и с переменными параметрами, коэффициенты а_i могут быть в общем случае функциями времени t. Если правая часть последнего уравнение равна тождественно нулю, т. е.

(a_npⁿ + a_n-1p^n-1 +…+ a₁p + a₀)y(t) = 0.  (12)

то такое уравнение называют однородным. Уравнение (11) называют соответственно неоднородным дифференциальным уравнением.

Уравнение (12) может иметь не более, чем п линейно независимых решений, n объектов называются линейно зависимыми, если по крайней мере один из них можно выразить в виде линейной комбинации остальных. В противном случае объекты считаются независимыми. Необходимое и достаточное ус­ловие линейной независимости n решений уравнения (11) состоит в отличии от нуля определителя Вронского. Если у₁, у₂,... у_n - n решений уравнения, то определитель Врон­ского имеет вид

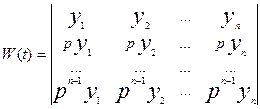        (13)

Общее решение уравнения (11) представляется как

y_н = K₁y₁ + K₂y₂ +…+ K_ny_n,  (14)

где K_i — произвольные постоянные. Индекс Н указывает на то, что решение соответствует однородному уравнению.

Из последнего уравнения следует, что если известны n независимых решений, то произвольное решение этого уравнения можно представить в виде линейной комбинация n известных решений. Для систем с постоянными параметрами существует общий метод

нахождения независимых решений однородного уравнения. Для систем с переменными параметрами такого метода, к сожалению, не существует.

Общее решение неоднородного уравнения (11) имеет вид У=У_н+У_p(15), где у_н — решение (14) соответствующего однородного уравнения, у_р - произвольное решение (вне зависимости оттого, каким образом оно получено), удовлетворяющее уравнению (11) и обычно называемое частным решением неоднородного уравнения, у_н называют вспомогательным решением. Для нахождения у_р приемлем любой способ, даже «метод проб». Так как у_р не содержит произвольных постоянные то в решении у, как и в у_н, содержится n постоянных.

Решение дифференциальных уравнений первого порядка

Линейной системой дифференциальных уравнений называется такая система уравнений, в которую неизвестные функции и их производные могут входить только в первой степени.

Нормальная линейная система дифференциальных уравнений имеет вид

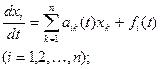(16)

Введем в рассмотрение векторные функции

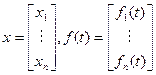 и матрицу  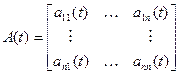   (17)

Тогда систему (1) можно переписать в виде

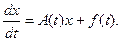    (18)

Теорема существования и единственности справедлива для линейной системы на любом отрезке [а₁ ,b₁]Ì(а, b), где (a, b) - интервал, на котором функции a_ik(t) и f_i(t) непрерывны.

Общее решение линейной однородной системы

Система (16) называется однородной, если f_i(t)º0 (i=1, 2, …, n). Однородная система в векторной форме запишется в виде

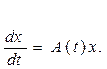  ⁽¹⁹⁾

Совокупность S всех решений {x(t)} образует линейное пространство размерности n, так как решения этой системы являются линейно-независимыми и образуют базис. Любой элемент этого пространства представим в виде

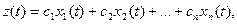         (20)

причем постоянные c₁, c₂, …, c_n определяются однозначно. Отсюда следует, что любое решение данной системы может быть представлено в виде (20). Поэтому выражение (20) называется общим решением системы (19). Любая система из n линейно-независимых решений системы (19), образующая базис пространства S, называется фундаментальной системой решений.

Физический смысл частного и вспомогательного решений.

Решение однородного уравнения (вспомогательное решение) зависит только от свойств системы и не зависит от входного воздействия. Характеристиче­ское уравнение зависит только от параметров системы, а корни характери­стического уравнения определяют вид составляющих вспомогательного ре­шения. В случае отсутствия внешних источников (т. е. система возбуждается запасенной в ней начальной энергией) вспомогательное решение совпадает с общим решением. Таким образом, вспомогательное решение характеризует «естественное» поведение системы при отсутствии внешних возмущений. В связи с этим вспомогательное решение называют также свободным или не ­вынужденными движением. Если вспомогательное решение системы неогра­ниченно возрастает при стремлении t к бесконечности, говорят, что система неустойчивая. Так как вспомогательное решение содержит экс­поненциаль­ные члены, то система станет неустойчивой, если ее характеристическое уравнение содержит корень с положительной действительной частью. С дру­гой стороны, корни с отрицательной действительной частью обусловливают стремление к нулю составляющих решения при стремлении t к бесконечности. При рассмотрении корней характеристического уравнения в комплексной плоскости можно сформулировать следующее утверждение. Если система устойчива, то ее корни должны лежать в левой полуплоскости, а на мнимой оси могут находиться только простые корни.

Если все корни характеристического уравнения лежат в левой полуплоскости, то вспомогательное решение стремится к нулю при стремлении t к бесконеч­ности и «совпадает» с переходным процессом в системе.

Величины составляющих во вспомогательном решении, т. е. произвольные постоянные решения, зависят от двух факторов, одним из которых является входной сигнал. Другим фактором служит предыстория системы (до момента приложения входного сигнала), которая полностью определяется знанием запасенной в системе энергии к моменту приложения входного воздействия. Вид частного решения обусловливается вынуждающей функцией; его легко усмотреть из метода неопределенных коэффициентов. Время влияет на вид решения лишь в том случае, если составляющая вынужденной функции сов­падает с каким-либо членом в у_н. Так как в этом случае система возбуждается на одной из ее собственных частот, то подобное явление называют резонан­сом.

В связи с тем, что вид част­ного ре­ше­ния зави­сит от вход­ного воз­дей­ствия, его назы­вают также вы­нуж­ден­ным дви­же­нием. Если все корни ха­рак­тери­сти­че­ского урав­нения лежат в ле­вой полу­плос­кости, вы­нуж­ден­ное ре­ше­ние сов­па­дает с уста­но­вив­шимся дви­же­нием. Ве­ли­чины вы­нуж­ден­ных со­став­ляю­щих зави­сят как от пара­мет­ров сис­темы, так и от вход­ного сиг­нала.

Обычно счи­тают, что вы­нуж­ден­ная со­став­ляю­щая ре­ше­ния уста­нав­лива­ется мгно­венно при по­даче вход­ного сиг­нала. Сво­бод­ная же со­став­ляю­щая, т. е. вспо­мога­тель­ное ре­ше­ние, как бы на­страивает себя путем пра­виль­ного опре­деле­ния про­из­воль­ных по­сто­ян­ных, чтобы обес­пе­чить над­ле­жа­щий пере­ход сис­темы из не­воз­буж­ден­ного со­стоя­ния в со­стоя­ние, под­чи­нен­ное вход­ному воз­дей­ствию.

Неко­торые склонны рас­смат­ри­вать вспо­мога­тель­ное ре­ше­ние как пер­вона­чаль­ное со­про­тив­ление сис­темы жела­ниям входа. Ве­ли­чины про­из­воль­ных по­сто­ян­ных зави­сят от того, на­сколько ха­рак­тер вход­ного воз­дей­ствия отли­ча­ется от «ес­тест­вен­ного» пове­дения сис­темы.

Линейная неоднородная система. Метод вариации произвольных постоянных.

Рассмотрим линейную неоднородную систему (18)

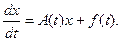
Соответствующая ей однородная система (19)

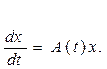
Пусть x=y(t) и j(t) – два решения системы (18). Тогда разность

x(t)= y(t)–j(t)

Представляет собой решение однородной системы (19).

Общее решение системы (18) имеет вид

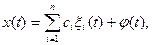
где c_i – произвольные постоянные; x_i(t) (i=1, 2, …, n) – фундаментальная система решений системы (19).

Частное решение системы (18) может быть найдено методом вариации произвольных постоянных. Рассмотрим этот метод. Пусть x₁(t), x₂(t), …, x_n(t)— фундаментальная система решений системы (19). Частное решение неоднородной системы (18) будем искать в виде

полагая, что c_i являются не постоянными, а некоторыми функ­циями t. Подставим это решение в систему (18):

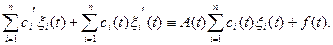
Так как вектор-функции x_i(t) – являются решениями однородной системы (19), то

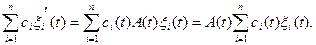
поэтому

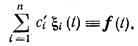
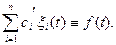
Это выражение представляет собой систему линейных алгебраи­ческих уравнений относительно сi(t) (i=l, 2, ,..., n). Определи­тель этой системы уравнений есть определитель Вронского для фундаментальной системы решений. Он отличен от нуля, поэтому эта система имеет единственное решение с_i’(t)=Ф_i(t) (i=l, 2,..., n).

Интегрируем полученные равенства:

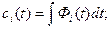
Следовательно, искомое частное решение имеет вид

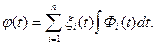
Значит, общее решение неоднородной системы будет

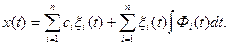
Дифференциальные уравнения систем автоматического регулирования.

Методика составления дифференциальных уравнений систем автоматического регулирования.

Общие замечания.

            Системы автоматического регулирования разнообразны по своему назначению и конструктивному исполнению. Поведение САР может описываться обыкновенными дифференциальными уравнениями в частных производных, разностными уравнениями и т.д.

            Любая САР представляет совокупность отдельных взаимодействующих друг с другом элементов, соединенных между собой связями. Первым этапом при составлении дифференциальных уравнений САР является разделение системы на отдельные элементы и составление дифференциальных уравнений этих элементов. Уравнения элементов и уравнения связей между отдельными элементами описывают процесс в системе регулирования, т.е. изменение по времени всех координат системы. Зная уравнения элементов и уравнения связей, можно составить структурную схему САР.

            Структурная схема САР характеризует геометрию системы, т.е. показывает, из каких элементов состоит САР и как эти элементы связаны между собой. Состояние САР, а также каждого входящего в нее элемента характеризуется некоторым числом независимых переменных. Этими переменными могут быть как электрические величины (ток, напряжение, и т.д.), так и механические (скорость, угол поворота, перемещение и т.д.). Обычно, чтобы характеризовать состояние системы или ее элемента, выбирают одну обобщенную координату на входе системы или элемента (g(t)) и одну – на выходе (x(t)). В ряде случаев такое представление невозможно, так как система или ее элемент могут иметь несколько входных и выходных величин. В многомерных системах можно рассматривать векторные входную и выходную величины с размерностями, совпадающими соответственно с числом входных и выходных величин САР.

Составление и линеаризация дифференциальных уравнений элементов систем.

            При составлении дифференциальных уравнений САР основной задачей является составление дифференциальных уравнений отдельных элементов системы. Уравнение отдельных элементов составляются на основе тех физических законов, которые характеризуют поведение элемента.

            При составлении дифференциальных уравнений элементов САР следует стремиться возможно точнее описать поведение данного элемента. Однако сложность получаемых при этом уравнений затрудняет исследование свойств их решений. Поэтому при составлении дифференциальных уравнений необходимо стремиться к разумному компромиссу между возможно более полным описанием поведения элемента и возможностью обозрения и исследования полученных уравнений.

            Если динамика элемента описывается линейным дифференциальным уравнением, то этот элемент называется линейным, если дифференциальное уравнение не линейно, то элемент называется нелинейным.

            Для упрощения анализа, когда это возможно, приближенно заменяют нелинейные дифференциальные уравнения такими линейными уравнениями, решение которых с достаточной степенью точности совпадают с решениями нелинейных уравнений. Этот процесс замены нелинейного дифференциального уравнения линейным называется линеаризацией.

            Если дифференциальное уравнение элемента нелинейно из-за нелинейности его статической характеристики, то линеаризация уравнения сводится к замене нелинейной характеристики элемента x=φ(g) некоторой линейной функцией x=ag+b. Аналитически эта замена производится с помощью разложения в ряд Тейлора функции x=φ(g) в окрестности точки, соответствующей установившемуся состоянию и отбрасывания всех членов содержащих отклонение ∆g входной величины элемента в степени выше первой. Геометрически это означает замену кривой x=φ(g) касательной, проведенной к кривой в точке (x₀, g₀), соответствующей установившемуся состоянию работы элемента (рис. 29). В других случаях линеаризация производится путем проведения секущей, мало отклоняющейся от функции x=φ(g) в требуемом диапазоне изменения входной величины элемента.

            Наряду с линеаризуемыми характеристиками имеются такие характеристики, которые не поддаются такой линеаризации. К ним относятся, например, характеристики, не разлагаемые в ряд Тейлора в окрестности точки установившегося состояния. Такие характеристики будем называть существенно нелинейными.

            Рассмотрим процесс линеаризации нелинейного уравнения элемента с помощью ряда Тейлора. Пусть поведение элемента описывается нелинейным дифференциальным уравнением

F(xⁿ, x^’, x, g) = 0 (1).

Тогда установившееся состояние элемента характеризуется уравнением F(0, 0, x, g) = 0 (2). пусть g₀ и х₀ – значения установившегося состояния. Тогда координаты g и х можно записать в виде x = x₀ + ∆x, g = g₀ + ∆g, где ∆g и ∆x – отклонение координат g и х от установившегося состояния. Уравнение (1) в отклонениях имеет вид:

F(∆x^’’, ∆x^’, x₀ + ∆x, g₀ + ∆g) = 0  (3).

            Разложим левую часть уравнения (3) в ряд Тейлора относительно точки установившегося состояния (0, 0, x₀, g₀):

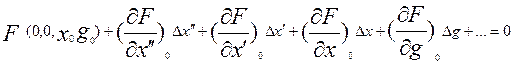 (4).

            Частные производные в левой части уравнения (4) представляют собой некоторые числа, величины которых зависят от вида функции F(x^’’, x^’, x, g) и значений координат x₀ и g₀.

            Считая отклонения ∆g, ∆x от установившегося состояния, а также их производные по времени малыми и пологая, что функция F(x^’’, x^’, x, g) достаточно гладкая по всем аргументам в окрестности точки, соответствующей установившемуся состоянию, отбросим в уравнении (4) все члены, которые содержат отклонения ∆g и ∆x, а также их производные в степени выше первой. Полученное уравнение 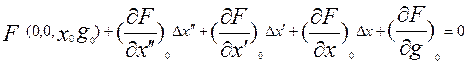 (5) является линейным дифференциальным уравнением с постоянными коэффициентами 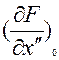, , ,  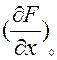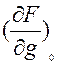и представляет собой результат линеаризации уравнения (1).

            Очевидно, что необходимым условием линеаризации является возможность разложения в ряд Тейлора функции F(x^’’, x^’, x, g) в окрестности точки, соответствующей установившемуся состоянию.

            Процесс линеаризации уравнения (1) может быть геометрически интерпретирован следующим образом. В пространстве переменных x^’’, x^’, x, g уравнение (1) задает некоторую поверхность. Переход от уравнения (1) к линейному уравнению (5) означает замену поверхности некоторой касательной плоскостью, проведенной к поверхности в точке, соответствующей установившемуся состоянию. Естественно, что ошибка при такой замене тем меньше, чем меньше отличаются друг от друга точки поверхности и точки плоскости. Это справедливо лишь в некоторой малой окрестности установившегося состояния.

Понятие пространства состояний

С точки зрения анализа и синтеза систем представляется целесообразным разделить все переменные, характеризующие систему, на три группы:

1) входные переменные или входные воздействия mi, представляющие сигналы, генерируемые системами, внешними по отношению к исследуемой, и влияющие на поведение системы;

2) выходные переменные или переменные, характеризующие реакцию системы y_j, позволяющие описать некоторые аспекты поведения системы, представляющие интерес для исследователя;

3) переменные (координаты) состояния или промежуточные переменные x_k, характеризующие динамическое поведение исследуемой системы.

Величины m_i, y_j и x_k предполагаются функциями времени. Для удобства оперирования с многомерными величинами совокупность входных переменных представим в виде вектора входа, совокупность выходных переменных – в виде вектора выхода, и совокупность переменных состояния – в виде вектора состояния:

.

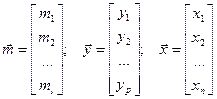Множество всех значений, которые может принять вектор входа m в момент t, образует пространство входа системы. Множество всех значений, которые может принять вектор выхода y в момент t, образует пространство выхода системы. Множество всех значений, которые может принять вектор состояния x в момент t, образует пространство состояний системы.

Понятие управляемости и наблюдаемости.

Управляемость: Пусть линейный многомерный процесс описывается векторным дифференциальным уравнением

dx(t)/dt=Ax(t)+Dm(t),        (1)

где x – n-мерный вектор состояния; m – r-мерный вектор, представляющий управляющие воздействия; A – квадратная матрица коэффициентов n-го порядка; D – матрица управления размера nxr.

Матрица A может быть приведена к диагональной матрице (или в общем случае к жордановой форме)

где l_ш – собственные значения матрицы A, которые предполагаются все различными.

Применяя подстановку x=Tz, исходное уравнение запишется в канонической форме

dz(t)/dt=Lz(t)+Dm(t),

где D=T^-1D=[d_ij]_nxr.

Вектор z в полученной формуле будем называть каноническим вектором состояния. Будем считать, что в предыдущих матричных выражениях собственные значения l_i расположены в порядке возрастания их модулей, комплексные l_i – в порядке возрастания их аргументов, векторы-столбцы матрицы T – нормализованы, то есть выбраны так, что евклидова длина их равна единице.

Запишем полученное выражение в развернутой форме, то есть в виде системы дифференциальных уравнений первого порядка:

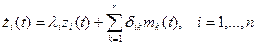
Эти уравнения показывают, что управляющее воздействие m_k не будет оказывать какого-нибудь влияния на движение по координате z_j, если

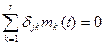
то есть когда d_jk=0 для k=1, 2, …, r. Запись в такой форме означает, что все элементы j-й строки матрицы D все равны нулю. Отсюда следует вывод, что неуправляемыми координатами системы являются все те канонические координаты, которые соответствуют нулевым строкам матрицы D. Равенство нулю всех элементов этих строк матрицы D делает невозможным управление по соответствующим координатам. Это означает также, что изменение координат происходит независимо от управляющих воздействий и, следовательно, целиком определяется начальными условиями и возмущениями. Можно сказать, что эти координаты развязаны от управления.

Приведенное рассмотрение позволяет дать следующее определение управляемости: процесс, описываемый уравнением (1), является полностью управляемым, если матрица D не содержит строк, элементы которых равны нулю; координаты, соответствующие ненулевым строкам D, считаются управляемыми.

Наблюдаемость: Перепишем еще раз выражение для вектора выхода линейного многомерного процесса:

y(t)=Bx(t)+Gm(t),        (1)

где y – p-мерный вектор, представляющий выходные переменные; B – матрица выхода размером pxn; G – матрица обхода системы размера pxr.

Пусть матрица B имеет вид

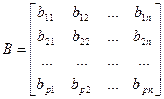
а матрица обхода G задана в виде

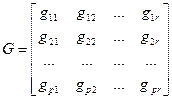
Тогда, развертывая формулу (1), получаем p выражений

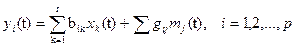      (2)

Координату состояния принято называть наблюдаемой, если она может быть определена или для нее может быть получена оценка по измеримым выходным переменным. Анализ уравнений (2) показывает, что координата x_k может быть определена или для нее может быть получена оценка по измеримым выходным переменным y₁, y₂, …, y_i, …, y_p, если коэффициенты b_ik для i=1, 2, …, p не все равны нулю. Другими словами, x_k является наблюдаемой координатой, если элементы k-го столбца матрицы выхода не все равны нулю. Если это условие не соблюдается, то координату x_k называют ненаблюдаемой. Таким образом, линейный процесс является наблюдаемым, если матрица выхода B не содержит столбцов, элементы которых равны нулю.

Соотношения вход – состояние – выход

            Пусть R – система, описываемая соотношением вход-выход вида

L(p)y = u₁ (1),

где L(p) = a_npⁿ +…+ a₀, a_n≠0 и a_i, 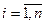 - постоянные, не обязательно вещественные. Тогда выражение для общего решения (1) будет

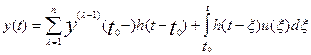, t ≥ t₀  (2)

где 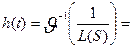импульсной реакции ,

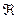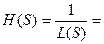       передаточной функции 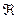,   (3)

         .

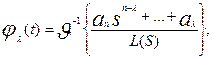
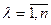            Функции времени φ₁,…, φ_n линейно независимые и удовлетворяют условию (дифференциальному уравнению)

L(p) φ_λ(t) = 0, ,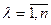

при начальных условиях

,

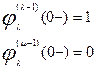для μ ≠ λ; μ,.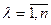

            Это значит, что они представляют собой множество (одностороннее) базисных функций .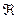

            Отождествим постоянные, появившиеся в (1), с составляющими вектора x(t₀) - состоянием 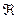 в момент времени t₀-. Наиболее естественным способом будет отождествление базисных функций с функциями φ₁,…, φ_n в (3). В этом случае составляющие x(t₀-), которые представляют собой коэффициенты базисных функций, будут

x₁(t_0-) = y₀(t₀-),

……………….

x_n(t_0-) = y^(n-1)(t₀-),

или в более компактной форме

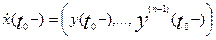. (4)

            Другой естественный способ состоит в том, чтобы положить базисные функции, или, точнее, их преобразования по Лапласу, равными

.

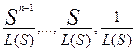            В этом случае составляющими x(t₀) будут

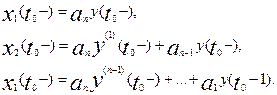(6)

            Рассмотрим случай, когда первая составляющая начального вектора состояния приравнена к выходу 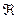 в моменты времени t₀-, вторая составляющая – первой производной выхода и т.д. Это значит, что вектор состояния в момент времени t представляется в виде

x(t) = (y(t),…, y^(n-1)(t)). (7)

Ради удобства вектор x(t), определенным с помощью (7), назовем нормальным вектором состояния 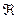, а соответствующие уравнения состояния – нормальными уравнениями для 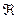. Пространство состояний, которому принадлежат х будет 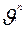, т.е. пространства упорядоченных наборов по n  комплексных чисел.

Уравнения состояния.

            Чтобы получить уравнение системы 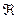 найдем выражение 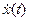, для чего продифференцируем  обе части равенства (7). В результате получим

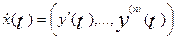. (8)

            С другой стороны из дифференциального уравнения (1) следует

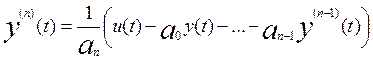
и, следовательно,

.

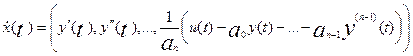            Это соотношение показывает, что составляющие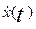 представляют собой линейные комбинации составляющих x(t) и u(t). Для представления этого соотношения в матричной форме обозначим через 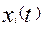и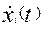, , 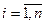i-ые составляющие 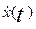 соответственно. Тогда из (8) следует

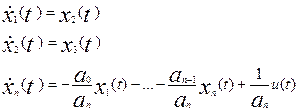
или в матричной форме

.

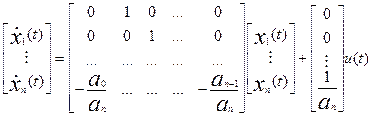            Последнее соотношение есть уравнение состояния в канонической форме 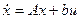, где А и b представляют собой соответственно, n×n матрицу с постоянными коэффициентами и n-мерный вектор.

            Таким образом, если x(t) задан с помощью (7), будучи определенным в 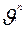, то x(t) удовлетворяет уравнению состояния (9). Этот результат совместно с соотношением

y(t) = x₁(t), или в матричной форме

.

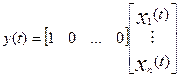            Пусть 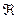 - обратно-дифференциально-операторная система, описываемая соотношением вход-выход-состояние

L(p)y = u, L(p) = a_npⁿ +…+ a₀, a_n≠0

            Тогда вектор 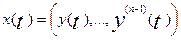 будет вектором состояния системы 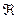 в момент времени t. При таком выборе x(t) уравнение для  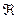будет

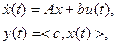 (10)

где

 , .

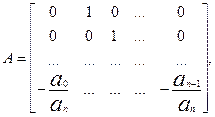
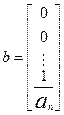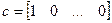            Соотношение вход-выход-состояние для 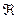 будет

  (11) 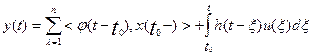  , t ≥ t₀ 

где

.

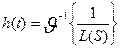
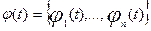
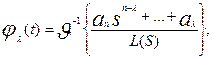
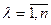
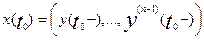Пример:

            Допустим, что система описывается уравнением

.

Тогда L(S) = S² + 3S + 2 = (S+1)(S+2)

и

,

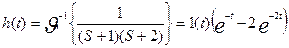
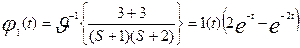
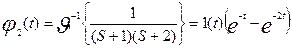где 1(t) обозначает единичную функцию.

            Соответствующие вектора состояния в момент времени t будут

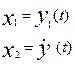
            Соответственно соотношение вход-выход-состояние можно записать в виде

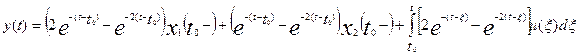, t ≥ t₀,

а матрицы и векторы будут

, , .

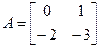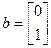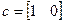Список литературы.

• Де Руссо, «Пространство состояний в теории систем»
• Чемоданов Б.К., «Математические основы теории автоматического регулирования», 1977
• Ту Ю., «Современная теория управления «Машиностроение», 1971
• Сю Д., Мейер А., «Современная теория автоматического управления и ее применение», 1972
• Заде Л., Дезоер Ч., «Теория линейных систем», 1970