ВСЕРОССИЙСКИЙ
ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА
СТАТИСТИКИ
О Т Ч
Е Т
о результатах выполнения
компьютерной лабораторной работы №2
«Автоматизированный корреляционно-регрессионный
анализ взаимосвязи статистических данных
в среде MS Excel»
Вариант № 52
Омск 2007
г.
1. Постановка задачи
Корреляционно-регрессионный
анализ взаимосвязи признаков является составной частью проводимого
статистического исследования и частично использует результаты Лабораторной
работы №1. В Лабораторной работе № 2
изучается взаимосвязь между факторным признаком Среднегодовая стоимость основных производственных фондов (признак Х) и результативным признаком Выпуск продукции (признак Y), значениями которых являются исходные данные
Лабораторной работы № 1 после исключения из них аномальных значений.
|
Номер предприятия
|
Среднегодовая стоимость
основных производственных фондов, млн.руб.
|
Выпуск продукции, млн.
руб.
|
|
|
1
|
2906,00
|
2781,00
|
|
2
|
3419,00
|
3051,00
|
|
3
|
3527,00
|
3402,00
|
|
4
|
3716,00
|
3780,00
|
|
5
|
2420,00
|
1890,00
|
|
6
|
3905,00
|
3240,00
|
|
7
|
4013,00
|
4374,00
|
|
8
|
3014,00
|
2970,00
|
|
9
|
3689,00
|
3483,00
|
|
10
|
4256,00
|
4347,00
|
|
11
|
4661,00
|
4590,00
|
|
13
|
3554,00
|
3618,00
|
|
14
|
3905,00
|
3942,00
|
|
15
|
4472,00
|
4779,00
|
|
16
|
5120,00
|
5130,00
|
|
17
|
3824,00
|
3456,00
|
|
18
|
4229,00
|
4104,00
|
|
19
|
3365,00
|
2565,00
|
|
20
|
4283,00
|
3510,00
|
|
21
|
4769,00
|
4725,00
|
|
22
|
3284,00
|
2673,00
|
|
23
|
2609,00
|
2511,00
|
|
24
|
4364,00
|
4023,00
|
|
25
|
3905,00
|
3510,00
|
|
26
|
3635,00
|
3321,00
|
|
27
|
2825,00
|
2160,00
|
|
28
|
3797,00
|
3375,00
|
|
29
|
4391,00
|
3699,00
|
|
30
|
4175,00
|
3510,00
|
|
32
|
3068,00
|
3132,00
|
|
|
|
|
В
процессе статистического исследования необходимо решить ряд задач.
1.
Установить
наличие стохастической связи между факторным признаком Х и результативным признаком Y:
а) графическим методом;
б) методом сопоставления параллельных рядов.
2.
Установить
наличие корреляционной связи между признаками Х и Y
методом аналитической группировки.
3. Оценить тесноту связи признаков Х и Y на основе:
а) эмпирического корреляционного отношения η;
б) линейного коэффициента корреляции r.
Сравнить значения η и r и сделать вывод о возможности линейной связи между
признаками Х и Y.
4. Построить однофакторную линейную регрессионную
модель связи признаков Х и Y, используя инструмент Регрессия надстройки Пакет анализа, и рассчитать
доверительные интервалы коэффициентов уравнения линейной регрессии.
Построить теоретическую кривую регрессии.
Дать экономическую интерпретацию коэффициента
регрессии.
Рассчитать коэффициент эластичности и дать его
экономическую интерпретацию.
5.
Найти наиболее
адекватное уравнение регрессии с помощью средств инструмента Мастер диаграмм.
II. Рабочий
файл с результативными таблицами и графиками.
|
|
Таблица 2.1
|
|
Исходные
данные
|
|
Номер предприятия
|
Среднегодовая стоимость основных производственных
фондов, млн.руб.
|
Выпуск продукции, млн. руб.
|
|
2420-2960
|
5
|
2420,00
|
1890,00
|
|
23
|
2609,00
|
2511,00
|
|
27
|
2825,00
|
2160,00
|
|
1
|
2906,00
|
2781,00
|
|
2960-3500
|
8
|
3014,00
|
2970,00
|
|
32
|
3068,00
|
3132,00
|
|
22
|
3284,00
|
2673,00
|
|
19
|
3365,00
|
2565,00
|
|
2
|
3419,00
|
3051,00
|
|
3500-4040
|
13
|
3554,00
|
3618,00
|
|
3
|
3527,00
|
3402,00
|
|
26
|
3635,00
|
3321,00
|
|
9
|
3689,00
|
3483,00
|
|
4
|
3716,00
|
3780,00
|
|
28
|
3797,00
|
3375,00
|
|
17
|
3824,00
|
3456,00
|
|
6
|
3905,00
|
3240,00
|
|
14
|
3905,00
|
3942,00
|
|
25
|
3905,00
|
3510,00
|
|
7
|
4013,00
|
4374,00
|
|
4040-4580
|
30
|
4175,00
|
3510,00
|
|
18
|
4229,00
|
4104,00
|
|
10
|
4256,00
|
4347,00
|
|
20
|
4283,00
|
3510,00
|
|
24
|
4364,00
|
4023,00
|
|
29
|
4391,00
|
3699,00
|
|
15
|
4472,00
|
4779,00
|
|
4580-5120
|
11
|
4661,00
|
4590,00
|
|
21
|
4769,00
|
4725,00
|
|
16
|
5120,00
|
5130,00
|
|
|
|
|
Таблица 2.2
|
|
Зависимость
выпуска продукции от среднегодовой стоимости основных фондов
|
|
Номер группы
|
Группы предприятий по стоимости основных фондов
|
Число предприятий
|
Выпуск продукции
|
|
Всего
|
В среднем
на одно
предприятие
|
|
1
|
2420-2960
|
4
|
10760,00
|
2690,00
|
|
2
|
2960-3500
|
5
|
16150,00
|
3230,00
|
|
3
|
3500-4040
|
11
|
41470,00
|
3770,00
|
|
4
|
4040-4580
|
7
|
30170,00
|
4310,00
|
|
5
|
4580-5120
|
3
|
14555,00
|
4851,67
|
|
Итого
|
|
30
|
113100,00
|
3770,00
|
|
|
|
Таблица 2.3
|
|
Показатели
внутригрупповой вариации
|
|
Номер группы
|
Группы предприятий по стоимости основных фондов
|
Число предприятий
|
Внутригрупповая дисперсия
|
|
1
|
2420-2960
|
4
|
155520,00
|
|
2
|
2960-3500
|
5
|
48600,00
|
|
3
|
3500-4040
|
11
|
104837,49
|
|
4
|
4040-4580
|
7
|
68040,00
|
|
5
|
4580-5120
|
3
|
116994,5
|
|
Итого
|
|
30
|
493991,99
|
|
|
|
Таблица 2.4
|
|
Показатели
дисперсии и эмпирического корреляционного отношения
|
|
Общая дисперсия
|
Средняя из внутригрупповых дисперсия
|
Межгрупповая дисперсия
|
Эмпирическое корреляционное отношение
|
|
586683,81
|
115731,27
|
470952,52
|
0,896
|
|
|
Таблица 2.5
|
|
Линейный
коэффициент корреляции признаков
|
|
|
Столбец 1
|
Столбец 2
|
|
Столбец 1
|
1
|
|
|
Столбец 2
|
0,91
|
1
|
Таблица
2.6
|
Выходные
таблицы
|
|
|
|
|
|
ВЫВОД
ИТОГОВ
|
|
|
|
|
|
|
|
|
Регрессионная статистика
|
|
|
|
|
Множественный R
|
0,91
|
|
|
|
R-квадрат
|
0,83
|
|
|
|
Нормированный R-квадрат
|
0,83
|
|
|
|
Стандартная ошибка
|
299,18
|
|
|
|
Наблюдения
|
30
|
|
|
Таблица
2.7
|
Дисперсионный
анализ
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
Регрессия
|
1
|
12583414,03
|
12583414,03
|
140,59
|
1,97601E-12
|
|
Остаток
|
28
|
2506190,13
|
89506,79
|
|
|
|
Итого
|
29
|
15089604,17
|
|
|
|
Таблица
2.8
|
|
Коэффи-
циенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 69,3%
|
Верхние 69,3%
|
|
Y-пересечение
|
-541,02
|
325,26
|
-1,66
|
0,11
|
-1207,29
|
125,26
|
-879,46
|
-202,57
|
|
Переменная X 1
|
1,09
|
0,09
|
11,86
|
1,97601E-12
|
0,90
|
1,28
|
0,99
|
1,19
|
|
ВЫВОД
ОСТАТКА
|
|
Таблица 2.9
|
|
|
|
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
|
1
|
1899,139357
|
-149,1393571
|
|
2
|
2089,776514
|
235,2234862
|
|
3
|
2307,64755
|
-307,64755
|
|
4
|
2389,349189
|
185,6508114
|
|
5
|
2498,284707
|
251,7152933
|
|
6
|
2552,752466
|
347,2475343
|
|
7
|
2770,623502
|
-295,6235019
|
|
8
|
2852,32514
|
-477,3251405
|
|
9
|
2906,7929
|
-81,79289952
|
|
10
|
3015,728418
|
134,2715824
|
|
11
|
3042,962297
|
307,0377029
|
|
12
|
3124,663936
|
-49,66393571
|
|
13
|
3179,131695
|
45,86830524
|
|
14
|
3206,365574
|
293,6344257
|
|
15
|
3288,067213
|
-163,0672129
|
|
16
|
3315,301092
|
-115,3010924
|
|
17
|
3397,002731
|
-397,002731
|
|
18
|
3397,002731
|
252,997269
|
|
19
|
3397,002731
|
-147,002731
|
|
20
|
3505,938249
|
544,061751
|
|
21
|
3669,341526
|
-419,3415262
|
|
22
|
3723,809285
|
76,19071476
|
|
23
|
3751,043165
|
273,9568352
|
|
24
|
3778,277044
|
-528,2770443
|
|
25
|
3859,978683
|
-134,9786829
|
|
26
|
3887,212562
|
-462,2125624
|
|
27
|
3968,914201
|
456,085799
|
|
28
|
4159,551358
|
90,44864238
|
|
29
|
4268,486876
|
106,5131243
|
|
30
|
4622,52731
|
127,4726905
|
III. Выводы по
результатам выполнения лабораторной работы.
Задача 1. Установление наличия стохастической связи
между факторным признаком Х и результативным
признаком Y:
а) графическим
методом.
Вывод: На основе анализа диаграммы рассеяния из
Лабораторной работы №1, полученной
после удаления аномальных значений, можно сделать вывод, что имеет место
стохастическая связь. Предположительный вид связи: линейная прямая.
б) методом
сопоставления параллельных рядов.
Вывод: Табл.2.1,
полученная путем ранжирования предприятий по возрастанию значения факторного
признака Х, показывает, что с
увеличением значений факторного признака увеличиваются значения результативного признака, за исключением
некоторых отклонений, что позволяет сделать вывод об обнаружении тесной
связи между признаками.
Задача 2. Установление наличия корреляционной связи
между признаками Х и Y методом
аналитической группировки.
Вывод: Результаты
выполнения аналитической группировки предприятий по факторному признаку Среднегодовая стоимость основных
производственных фондов даны в табл. 2.2 Рабочего файла, которая
показывает, что для каждой выделенной группы подсчитывается численность
составляющих ее факторных значений, а также
суммарные и средние групповые значения результативного признака. В
данном случаи между признаками
прямая и тесная связь.
Задача 3.Оценка тесноты связи признаков Х и Y:
а)
на основе эмпирического
корреляционного отношения
Для анализа тесноты связи между факторным и
результативным признаками, рассчитывается показатель η - эмпирическое корреляционное отношение, задаваемое
формулой
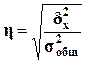
Для вычисления η необходимо знать общую
дисперсию 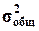 и межгрупповую
дисперсию
и межгрупповую
дисперсию 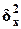 результативного
признака Y - Выпуск
продукции.
результативного
признака Y - Выпуск
продукции.
Результаты выполненных расчетов
представляются табл. 2.4 Рабочего файла.
Вывод: Величина η=0,896 является близкой к единице, что свидетельствует о
том, что корреляционная зависимость
полная , т.е. функциональная ( т.е. означает, что отсутствие влияния на Y любых иных, кроме X, факторов)
б)
на основе линейного коэффициента
корреляции признаков
В
предположении, что связь между факторным и результативным признаком имеется,
для определения тесноты связи на основе линейного коэффициента корреляции r был
использован инструмент Корреляция
надстройки Пакет анализа.
Результатом
работы инструмента Корреляции
является табл. 2.5 Рабочего файла.
Вывод: Значение коэффициента корреляции r=0,91 интервале 0,9-0,99 , что в
соответствии со шкалой Чэддока, говорит о весьма высоком значении.
Так как значение коэффициента
корреляции r положительное,
то связь между признаками соответствует линейной прямой зависимости.
Посредством
показателя η измеряется
теснота связи любой формы, а с помощью коэффициента корреляции r – только прямолинейная,
следовательно, значения η и r совпадают только при наличии
прямолинейной связи. В теории статистики установлено, что если 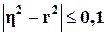 , то гипотезу о прямолинейной связи можно считать
подтвержденной.
, то гипотезу о прямолинейной связи можно считать
подтвержденной.
Вывод: :
В данном случаи действие 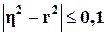 выполняется, а значит, гипотеза о прямолинейной связи
подтверждается.
выполняется, а значит, гипотеза о прямолинейной связи
подтверждается.
Задача 4. Построение однофакторной линейной регрессионной
модели связи изучаемых признаков с помощью инструмента Регрессия надстройки
Пакет анализа.
Построение
регрессионной модели заключается в определении аналитического выражения
связи между факторным признаком X
и результативным признаком Y.
Инструмент
Регрессия производит расчет
параметров а0 и а1 уравнения
однофакторной линейной регрессии 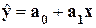 и проверка его адекватности исследуемым
фактическим данным.
и проверка его адекватности исследуемым
фактическим данным.
В
результате работы инструмента Регрессия
были получены результативные таблицы 2.6 – 2.9 Рабочего файла.
Вывод: Однофакторная линейная
регрессионная модель связи факторного и результативного признаков имеет вид:
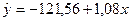
Доверительные интервал
коэффициентов уравнения регрессии представим в нижеследующей таблице
|
Коэффициенты
|
Границы доверительных интервалов
|
|
С надежностью Р=0,68
|
С надежностью Р=0,95
|
|
Нижние
|
Верхние
|
Нижние
|
Верхние
|
|
а0
|
-200,39
|
-174,48
|
-1012,08
|
106,66
|
|
а1
|
0,99
|
1,18
|
0,9
|
1,27
|
С
увеличением надежности границы доверительных интервалов не изменится, так
как они являются приближенными.
Экономическая интерпретация коэффициента регрессии – это перевод модели с языка
статистики и математики на язык экономики. Интерпретация уравнения регрессии используется для целей
анализа и прогноза взаимосвязей.
Коэффициент эластичности 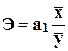 =
=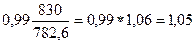
Экономическая
интерпретация коэффициента эластичности показывает на сколько процентов изменяется
а среднем результативный признак при изменении факторного признака на 1%.
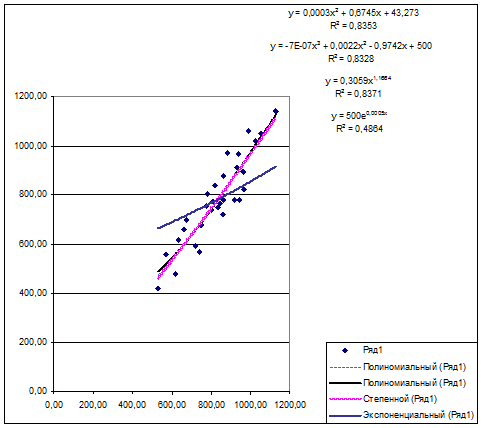
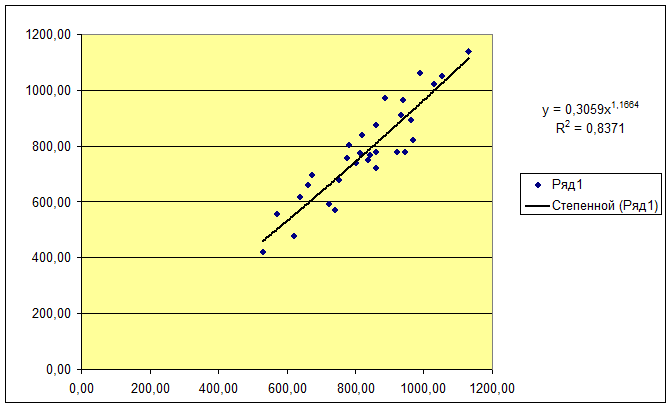
Задача 5.
Нахождение наиболее адекватного
уравнения регрессии с помощью средств инструмента Мастер диаграмм. Построение для этого уравнения теоретической
линии регрессии.
Возможности инструмента Мастер диаграмм позволяют быстро производить построение и анализ
адекватности регрессионных моделей, базирующихся на использовании различных
видов зависимости между признаками X и Y.
Построение моделей осуществляется непосредственно
на диаграмме рассеяния.
На диаграмме рассеяния отображается линия и
уравнение регрессии, а также коэффициент детерминации R2.
В лабораторной работе уравнения регрессии и их
графики были построены для 5-ти видов зависимости между признаками и даны на
диаграмме Рабочего файла.
Уравнения регрессии и соответствующие им
коэффициент детерминации R2 даны в следующей
таблице:
Регрессионные
модели связи
|
Вид уравнения
|
Уравнение регрессии
|
Коэффициент
детерминации R2
|
|
Линейное
|
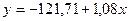
|
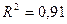
|
|
Полином 2-го порядка
|

|
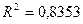
|
|
Полином 3-го порядка
|
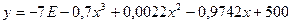
|
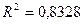
|
|
Степенное
|
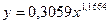
|
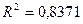
|
|
Экспоненциальное
|
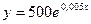
|
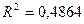
|
Выбор
наиболее адекватного уравнения регрессии определяется максимальным значением
коэффициента детерминации R2: чем ближе значение R2 к единице, тем более точно регрессионная модель
соответствует фактическим данным
Вывод: Максимальное
значение коэффициента детерминации R2 =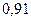 .
.
Вид
искомого уравнения регрессии –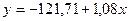
Это
уравнение регрессии и его график приведены на отдельной диаграмме рассеяния
Рабочего файла.
Вместе с тем, так как значения коэффициентов R2 кубического
и линейного уравнения расходятся очень незначительно (на величину 0,0747), а
для показателей тесноты связи имеет место неравенство 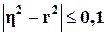 , то в качестве адекватного уравнения регрессии может быть
принято линейное уравнение
, то в качестве адекватного уравнения регрессии может быть
принято линейное уравнение 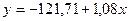 совпадающее с найденным с помощью
инструмента Регрессия надстройки Пакет анализа.
совпадающее с найденным с помощью
инструмента Регрессия надстройки Пакет анализа.