Вариант №6
Задание 1.
Имеются следующие отчетные данные 24 заводов одной из отраслей промышленности:
|
№ завода |
Среднегодовая стоимость ОПФ, млн. руб |
Валовая продукция в сопоставимых ценах, млн. руб |
|
1 |
1.6 |
1.5 |
|
2 |
3.9 |
4.2 |
|
3 |
3.3 |
4.5 |
|
4 |
4.9 |
4.4 |
|
5 |
3.0 |
2.0 |
|
6 |
5.1 |
4.2 |
|
7 |
3.1 |
4.0 |
|
8 |
0.5 |
0.4 |
|
9 |
3.1 |
3.6 |
|
10 |
5.6 |
7.9 |
|
11 |
3.5 |
3.3 |
|
12 |
0.9 |
0.6 |
|
13 |
1.0 |
1.1 |
|
14 |
7.0 |
7.5 |
|
15 |
4.5 |
5.6 |
|
16 |
8.1 |
7.6 |
|
17 |
6.3 |
6.0 |
|
18 |
5.5 |
8.4 |
|
19 |
6.6 |
6.5 |
|
20 |
1.0 |
0.9 |
|
21 |
4.7 |
4.5 |
|
22 |
2.7 |
2.3 |
|
23 |
2.9 |
3.2 |
|
24 |
6.8 |
6.9 |
С целью изучения зависимости между среднегодовой стоимостью ОПФ и выпуском валовой продукции произведите группировку заводов по среднегодовой стоимости ОПФ, образовав 4 группы заводов с равными интервалами. По каждой группе и совокупности заводов подсчитайте:
1. Число заводов.
2. Среднегодовую стоимость основных фондов – всего и в среднем на один завод.
3. Стоимость валовой продукции – всего и в среднем на один завод.
4. Размер валовой продукции на один рубль ОПФ (фондоотдачу).
Результат представить в виде групповой таблицы.
Решение.
Стоимость ОПФ мин. = 0.5
Стоимость ОПФ макс = 8.1
Размах = 8.1–0.5 = 7.6
Границы интервалов.
0.5+7.6·![]() = 0.5+1.875 = 2.475
= 0.5+1.875 = 2.475
0.5+7.6·![]() = 0.5+3.75 = 4.25
= 0.5+3.75 = 4.25
0.5+7.6·![]() = 0.5+5.625 = 6.225
= 0.5+5.625 = 6.225
Получаем следующие интервалы:
1 – (0.5; 2.475)
2 – (2.475; 4.25)
3 – (4.25; 6.225)
4 – (6.225; 8.1)
1. Число заводов.
1 группа – 5 заводов.
2 группа – 8 заводов.
3 группа – 6 заводов.
4 группа – 5 заводов.
2. Среднегодовая стоимость основных фондов.
По первой группе.
Всего.
0.5+0.9+1+1+1.6 = 5.1
В среднем на один завод
5.1/5 = 1.04
По второй группе.
Всего.
2.7+3+3.0+3.1+3.1+3.3+3.5+4 = 26.3
В среднем на один завод
26.3/8 = 3.1875
По третьей группе.
Всего.
4.5+4.7+5+5.1+5.5+5.6 = 30.5
В среднем на один завод
30.5/6 = 5.1
По четвертой группе.
Всего.
6.3+6.6+6.8+7+8.1 = 34.9
В среднем на один завод
34.9/5 = 6.88
По всей совокупности заводов.
Всего.
5.1+26.3+30.5+34.9 = 97
В среднем на один завод
97/24 = 3.942
3. Средняя стоимость валовой продукции
По первой группе.
Всего.
0.4+0.5+1.1+0.7+1.6 = 4.5
В среднем на один завод
4.5/5 = 0.88
По второй группе.
Всего.
2.6+3.3+2.1+4.2+3.7+4.6+3.3+4.2 = 28.2
В среднем на один завод
28.2/8 = 3.525
По третьей группе.
Всего.
5.6+4.5+4.5+4.5+8.4+7.5 = 34.9
В среднем на один завод
34.9/6 = 5.817
По четвертой группе.
Всего.
6+6.4+7+7.5+7.6 = 34.5
В среднем на один завод
34.5/5 = 6.8
По всей совокупности заводов.
Всего.
4.5+28.2+34.9+34.5 = 102
В среднем на один завод
102/24 = 4.25
4. Фондоотдача.
По первой группе.
4.5/5.1 = 0.846
По второй группе.
28.2/26.3 = 1.072
По третьей группе.
34.9/30.5 = 1.14
По четвертой группе.
34.5/34.9 = 0.988
Всего
102/97 = 1.052
|
Группа |
Число заводов |
Стоимость основных фондов |
Стоимость валовой продукции |
Фондо-отдача |
||
|
Всего |
На 1 завод |
Всего |
На 1 завод |
|||
|
1 |
5 |
5.1 |
1.04 |
4.5 |
0.88 |
0.846 |
|
2 |
8 |
26.3 |
3.1875 |
28.2 |
3.525 |
1.072 |
|
3 |
6 |
30.5 |
5.1 |
34.9 |
5.817 |
1.14 |
|
4 |
5 |
34.9 |
6.88 |
34.5 |
6.8 |
0.988 |
|
Всего |
24 |
97 |
3.942 |
102 |
4.25 |
1.052 |
Вывод. Наблюдается однонаправленное изменение средних групповых значений факторного и результативного признаков: при увеличении стоимости основных фондов увеличивается стоимость валовой продукции. Следовательно, приходим к выводу о наличии взаимосвязи между исследуемыми признаками.
Задание 2.
Имеются следующие данные по двум группам заводов промышленного объединения:
|
Первая группа |
Вторая группа |
||||
|
№ завода |
Фактический выпуск продукции, млн. руб. |
Выполнение плана выпуска продукции, % |
№ завода |
Плановое задание выпуска продук-ции, млн. руб. |
Выполнение плана выпуска продукции, % |
|
1 |
23 |
100 |
3 |
20 |
97 |
|
2 |
21 |
105 |
4 |
22 |
110 |
Вычислите средний процент выполнения плана выпуска продукции:
1. Первой группы заводов.
2. Второй группы заводов.
Укажите, какой вид средней надо применить для вычисления этих показателей.
Сравните средние проценты выполнения плана двух групп заводов.
Решение.
Для решения задачи необходимо пользоваться средней гармонической взвешенной.[1]
1. Найдем план по выпуску продукции на первом заводе. Он будет равен 23/1.02 = 22.12 млн. руб.
План по выпуску продукции на втором заводе. 21/1.07 = 18.97 млн. руб.
Средний процент выполнения плана выпуска продукции по первой группе заводов равен (23+21)/(22.12+18.97) = 1.04 = 104%.
2. Найдем фактический выпуск продукции на третьем заводе. Он будет равен 20·0.97 = 18.8 млн. руб.
Фактический выпуск продукции на четвертом заводе. 22·1.1 = 24.2 млн. руб.
Для нахождения среднего процента выполнения плана продукции по группам заводов воспользуемся формулой среднего арифметического.
Средний процент выполнения плана выпуска продукции по второй группе заводов равен (18.8+24.2)/(20+22) = 1.03 = 103%
Получаем, что на первой группе заводов показатель выполнения плана лучше.
Задание 3.
С целью изучения обеспеченности населения области предприятиями общественного питания проведена 5%-ная механическая выборка, в результате которой получено следующее распределение предприятий общепита по числу посадочных мест:
|
Группы предприятий по числу посадочных мест, единиц |
Удельный вес числа предприятий, % |
|
До 25 |
15 |
|
25-50 |
20 |
|
50-75 |
35 |
|
75-100 |
25 |
|
Свыше 100 |
5 |
|
Итого |
100 |
На основе этих данных вычислите:
1. Среднее число посадочных мест на одно предприятие.
2. Средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение.
3. Коэффициент вариации.
4. С вероятностью 0,997 предельную ошибку выборочной средней и возможные границы, в которых ожидается среднее число мест на одно предприятие области.
5. С вероятностью 0,997 предельную ошибку выборочной доли и границы удельного веса числа предприятий с числом посадочных мест от 25 до 100.
Решение.
Перепишем таблицу в виде: среднее число посадочных мест и количество предприятий:
|
Среднее число посадочных мест |
12.5 |
37.5 |
62.5 |
87.5 |
112.5 |
|
Число предприятий |
15 |
20 |
35 |
25 |
5 |
1. Среднее число посадочных мест.
![]() = (12.5·15+ 37.5·20+ 62.5·35+ 87.5·25 + 112.5·5)/100 = (125+ 937.5+
2187.5+ 1750+ 1125)/100 = 6125/100 = 61.25
= (12.5·15+ 37.5·20+ 62.5·35+ 87.5·25 + 112.5·5)/100 = (125+ 937.5+
2187.5+ 1750+ 1125)/100 = 6125/100 = 61.25
2. Дисперсия.
D(X) = (((12.5-61.25)2·10+ (37.5-61.25)2·25+ (62.5-61.25)2·35+ (87.5-61.25)2·20+ (112.5-61.25)2·10)/100 = ((48.752·10+ 23.752·25+ 1.252·35+ 26.252·20+ 51.252·10)/100 = (2376.5625·10+ 564.0625·25+ 1.5625·35+ 689.0625·20+ 2626.5625·10)/100 = (23765.625+ 14101.5625+ 54.6875+ 13781.25+ 26265.625)/100 = 77968.75/100 = 779.6875
Среднеквадратическое отклонение.
![]()
3. Коэффициент вариации.
![]()
4. Предельная ошибка выборочной средней равна
![]() =
= ![]() = 2.8.
= 2.8.
Для вероятности 0.997 коэффициент доверия равен t=3.
Предельная ошибка среднего значения равна Δ=t·μ = 3·2.8=8.4
Границы, в которых с вероятностью 0.997 лежит среднее число мест на одно предприятие равны
(61.25–8.4; 61.25+8.4)
(52.85; 69.65)
5. Для вероятности p=0.997 коэффициент доверия t=3. Найдем предельную ошибку при данных условиях.
Для нахождения w разделим количество предприятий, удовлетворяющих условию на общее число предприятий.
![]()
![]() =
= ![]() =
= ![]() = 0.117
= 0.117
Искомый интервал с вероятностью 0.997
(0.8–0.117; 0.8+0.117)
(0.683; 0.917)
Задание 4.
Производство пылесосов в СССР характеризуется следующими данными:
|
Годы |
Выпуск, млн. шт. |
|
1980 |
3.2 |
|
1981 |
3.4 |
|
1982 |
3.5 |
|
1983 |
3.6 |
|
1984 |
3.8 |
|
1985 |
4.1 |
Для анализа динамики производства электропылесосов за 1980-1985 гг. вычислите:
1. Абсолютные приросты, темпы роста и прироста по годам и к 1980 г., абсолютное содержание одного процента прироста. Полученные показатели представьте в таблице.
2. Среднегодовое производство пылесосов.
3. Среднегодовой темп роста и прироста производства пылесосов.
Постройте график динамики производства электропылесосов в СССР за 1980-1985 гг.
Сделайте выводы.
Решение.
|
Год |
Выпуск пылесосов |
Абсолютный прирост |
Темп роста |
Темп прироста |
Абсолютное содержание 1%прироста |
|||
|
за год |
к 1980 г. |
за год |
к 1980 г. |
за год |
к 1980 г. |
|||
|
1980 |
3.2 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
1981 |
3.4 |
0.2 |
0.2 |
1.038 |
1.038 |
0.038 |
0.038 |
0.05263 |
|
1982 |
3.5 |
0.1 |
0.3 |
1.019 |
1.058 |
0.019 |
0.058 |
0.05263 |
|
1983 |
3.6 |
0.1 |
0.4 |
1.018 |
1.077 |
0.018 |
0.077 |
0.05556 |
|
1984 |
3.8 |
0.2 |
0.6 |
1.036 |
1.115 |
0.036 |
0.115 |
0.05556 |
|
1985 |
4.1 |
0.3 |
0.9 |
1.052 |
1.173 |
0.052 |
0.173 |
0.05769 |
Среднегодовое производство пылесосов.
(3.2+3.4+3.5+3.6+3.8+4.1)/6 = 21.6/6 = 3.6
Среднегодовой темп роста
![]() = 1.0324
= 1.0324
Среднегодовой темп прироста.
0.9/5 = 0.18
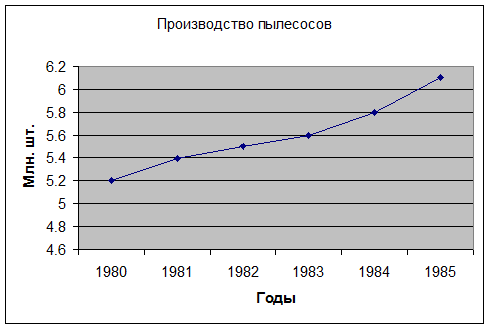
Вывод: в среднем производство пылесосов в стане за период с 1980 по 1985 год возрастало на 0.18 млн. шт. или в 1.0324 раза.
Задание 5.
Имеются следующие данные об остатках товаров в розничном торговом предприятии:
|
|
1 января |
1 февраля |
1 марта |
1 апреля |
1 мая |
1 июня |
1 июля |
|
Остатки товаров на начало месяца, млн. руб. |
50.2 |
51.4 |
53.6 |
52.8 |
51.6 |
50.8 |
50.0 |
Вычислите среднемесячные остатки товаров:
1. За первый квартал.
2. За второй квартал.
3. За полугодие.
Поясните, почему методы расчета средних уровней рядов динамики в задаче 4 и 5 различны.
Решение.
Среднемесячные остатки товаров за первый квартал
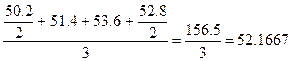
Среднемесячные остатки товаров за второй квартал
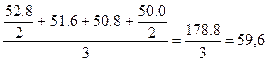
Среднемесячные остатки товаров за полугодие
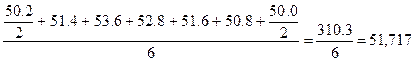
В задаче 4 был использован интервальный ряд динамики, а в задаче 5 – моментный.
Задание 6.
Динамика себестоимости и объема производства продукции заводов характеризуется следующими данными:
|
Вид продукции |
Выработано продукции, тыс. шт. |
Себестоимость единицы продукции, тыс. руб. |
||
|
Базисный период |
Отчетный период |
Базисный период |
Отчетный период |
|
|
Завод №1 |
|
|
|
|
|
ВН-25 |
2500 |
3000 |
14.0 |
13.0 |
|
НС-26 |
5000 |
6000 |
18.0 |
17.0 |
|
Завод №2 |
|
|
|
|
|
ВН-25 |
4000 |
5000 |
16.0 |
15.0 |
На основании имеющихся данных вычислите:
1. Для завода №1 (по двум видам продукции вместе):
а) общий индекс затрат на производство продукции;
б) общий индекс себестоимости продукции;
в) общий индекс физического объема производства продукции.
Определите в отчетном периоде изменение суммы затрат на производство продукции и разложите по факторам (за счет изменения себестоимости и объема выработанной продукции).
Покажите взаимосвязь между исчисленными индексами.
2. Для двух заводов вместе (по продукции ВН-25):
а) индекс себестоимости переменного состава;
б) индекс стоимости постоянного состава;
в) индекс влияния изменения структуры производства продукции на динамику средней себестоимости.
Объясните разницу между величинами индексов переменного и постоянного состава.
Решение.
Обозначим z0, z1 – себестоимость продукции в базисном и отчетном периодах.
q0, q1 – количество продукции базисном и отчетном периодах.
Общий индекс затрат на производство продукции.
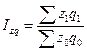 =
= ![]() = 0.8586
= 0.8586
Общий индекс себестоимости продукции.
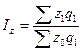 =
= ![]() = 0.9034
= 0.9034
Общий индекс физического объема производства продукции
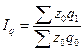 =
= ![]() = 0.9504
= 0.9504
Изменение затрат на производство 39.3–45.77=–6.47 млн. руб.
Изменение затрат за счет изменения себестоимости 39.3–43.5=–4.2 млн. руб.
Изменение затрат за счет изменения объема продукции 43.5–45.77=–2.27 млн. руб.
Связь между индексами.
Izq=Iz·Iq
2. Индекс переменного состава.
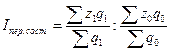 =
= ![]() = 1.0563
= 1.0563
Индекс постоянного состава.
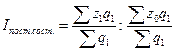 =
= ![]() = 1.0499
= 1.0499
Индекс влияния изменения структуры производства продукции на динамику средней себестоимости
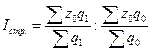 =
= ![]() = 1.006/
= 1.006/
Индекс переменного состава – это отношение двух средних величин, Он учитывает одновременно и структурные изменения в составе совокупности, и изменение уровня самого осредняемого признака у отдельных объектов.
Индекс постоянного или фиксированного состава – отражает изменение среднего уровня качественного показателя под влиянием изменения самого качественного показателя у отдельных единиц совокупности.
Задание 7.
Для изучения тесноты связи между выпуском валовой продукции на один завод (результативный признак Y) и оснащенностью заводов основными производственными фондами (факторный признак – Х) по данным задания 1 вычислите коэффициент детерминации и эмпирическое корреляционное отношение. Поясните их значение.
Решение.
Решение оформим в виде вспомогательной таблицы:
|
№ завода |
X |
Y |
XY |
X2 |
Y2 |
|
1 |
1.6 |
1.5 |
2.4 |
2.56 |
2.25 |
|
2 |
3.9 |
4.2 |
16.38 |
15.21 |
17.64 |
|
3 |
3.3 |
4.5 |
14.85 |
10.89 |
20.25 |
|
4 |
4.9 |
4.4 |
21.56 |
24.01 |
19.36 |
|
5 |
3.0 |
2.0 |
6 |
9 |
4 |
|
6 |
5.1 |
4.2 |
21.42 |
26.01 |
17.64 |
|
7 |
3.1 |
4.0 |
12.4 |
9.61 |
16 |
|
8 |
0.5 |
0.4 |
0.2 |
0.25 |
0.16 |
|
9 |
3.1 |
3.6 |
11.16 |
9.61 |
12.96 |
|
10 |
5.6 |
7.9 |
44.24 |
31.36 |
62.41 |
|
11 |
3.5 |
3.3 |
11.55 |
12.25 |
10.89 |
|
12 |
0.9 |
0.6 |
0.54 |
0.81 |
0.36 |
|
13 |
1.0 |
1.1 |
1.1 |
1 |
1.21 |
|
14 |
7.0 |
7.5 |
52.5 |
49 |
56.25 |
|
15 |
4.5 |
5.6 |
25.2 |
20.25 |
31.36 |
|
16 |
8.1 |
7.6 |
61.56 |
65.61 |
57.76 |
|
17 |
6.3 |
6.0 |
37.8 |
39.69 |
36 |
|
18 |
5.5 |
8.4 |
46.2 |
30.25 |
70.56 |
|
19 |
6.6 |
6.5 |
42.9 |
43.56 |
42.25 |
|
20 |
1.0 |
0.9 |
0.9 |
1 |
0.81 |
|
21 |
4.7 |
4.5 |
21.15 |
22.09 |
20.25 |
|
22 |
2.7 |
2.3 |
6.21 |
7.29 |
5.29 |
|
23 |
2.9 |
3.2 |
9.28 |
8.41 |
10.24 |
|
24 |
6.8 |
6.9 |
46.92 |
46.24 |
47.61 |
|
Сумма |
97 |
102 |
522.39 |
469.1 |
567.56 |
|
Среднее |
4,04 |
4,25 |
21.77 |
20.67 |
23.65 |
D(X) = 20.67-4.042 =20.67-16.3216=4.3484
![]()
D(Y) = 23.65-4.252 =23.65-18.0625=5.5875
![]()
Коэффициент корреляции.
![]() =
= ![]() =
= ![]() = 0.9326
= 0.9326
Коэффициент детерминации
R2 = 0.93262 = 0.8697
Это значение коэффициента детерминации говорит о том, что 86.97% изменения результативного признака объясняется изменением факторного признака.
Рассчитаем межгрупповые дисперсии.
Условные средние.
![]() = 1.04
= 1.04
![]() = 3.29
= 3.29
![]() = 5.1
= 5.1
![]() = 6.98
= 6.98
![]() = 0.88
= 0.88
![]() = 3.53
= 3.53
![]() = 5.82
= 5.82
![]() = 6.9
= 6.9
Межгрупповые дисперсии.
![]() =
= ![]() =
= ![]() = 2.7
= 2.7
![]() =
= ![]() =
= ![]() = 4.618
= 4.618
![]()
![]()
Эмпирические корреляционные отношения.
![]()
![]()
Это говорит о том, что связь между переменными весьма тесная.
[1] Нехорошков С.Б., Макаридина Е.В. Статистика. Сборник задач с методическими указаниями. – Новосибирск, СибАГСЮ 2001. – с. 12.