Численные методы

Контрольная работа

Приближённые числа и действия над ними

Задание 1.

1. Определить какое равенство точнее.

2. Округлить сомнительные цифры числа, оставив верные знаки: а) в узком смысле; б) в широком смысле. Определить абсолютную погрешность результата.

3. Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры: а) в узком смысле; б) в широком смысле.

1)  = 6,63; 19 / 41 = 0,463.

2) а) 22,553 (0,016); б) 2,8546;  = 0,3%.

3) а) 0,2387; б) 42,884.

Решение.

1. = 6,6332495

= 0,0032495

= 0,00041463

 = 0,0005

 = 0,0009

19 / 41 = 0,46341463

, тем не менее точнее первое равенство, ведь

2. Решение.

а) 22, 553 + = 22,553 + 0,016 = 22,569;

22,553 - = 22,537.

Значит, 22,553 22,5.

б)  * 100% = 0,3%

 = 0,003

= 2,8546 *  = 0,0086

2,8546 ≈ 2,8.

3. Решение.

а)  = 0,000099…

б)  = R * 10^-5;

% = 20 * 10^-3 % = 0,002%.

Задание 2.

Вычислить и определить погрешности результата.

 где а = 3,85 (0,01), b = 2,0435 (0,0004), с = (0,1).

Решение.

Х = 0,7968.

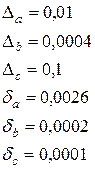
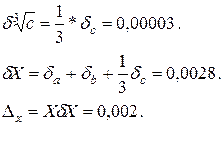
Значит, Х ≈ 0,797.

Х = 0,797 ( 0,002).

Приближённые решения алгебраических и трансцендентных уравнений

Отделить корни уравнения аналитически или графически и уточнить один из них с точностью до 0,001:

а) методом половинного деления;

б) методом хорд и методом касательных;

в) комбинированным методом;

г) методом итераций.

а) 3х⁴ + 4х³ – 12х² – 5 =0

б) х – sin х = 0,25

в) 2х³ – 3х² – 12х – 5 = 0

г) ln х + (х + 1)³ = 0.

Решение.

 

а) графический способ трудоёмкий, отделяем корни аналитически:

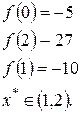
Следовательно,

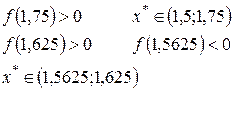
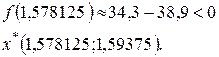
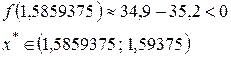
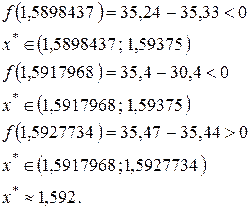
б) х – sin х = 0,25.

 

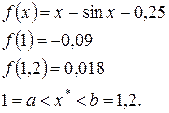
При методе хорд:

х_n+1 =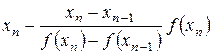

х₀ = b -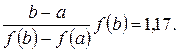

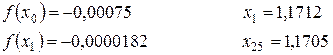
Уже видно, что х^* = 1,171.

Метод касательных:

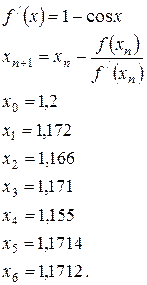
Видно, что х^* = 1,171.

в) 2х³ – 3х² – 12х – 5 = 0.

При переборе х для отделения корней получаем, что х^* = - 0,5 – точный корень.

При этом уравнение принимает вид (х + ½) (2х² – 4х + 10) = 0.

Выясняется, что х^* = -0,5 – единственный корень. Комбинированный метод теряет смысл, т.к. можно взять х₀ = -0,5 и процесс итераций тут же заканчивается.

г) ln х + (х + 1)³ = 0

ln х = - (х + 1)³

х =

		х

 

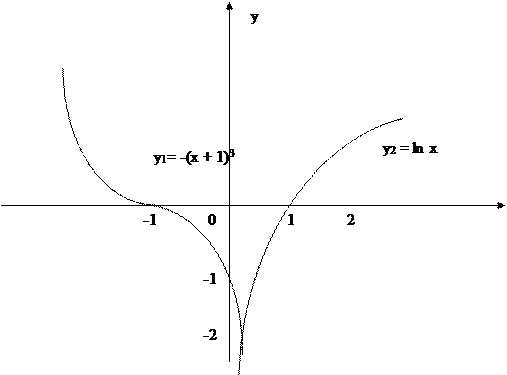Есть единственный корень х^*, 0 < х^* <0,25.

Интерационный процесс:

х_n+1 =

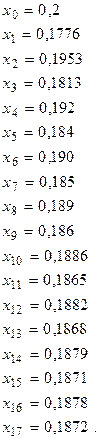
Уже видно, что х^* = 0,187.

Решение систем линейных алгебраических уравнений

Решить систему линейных алгебраических уравнений методом простой итерации и методом Зейделя.

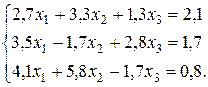
Решение.

Матрица системы имеет вид

А =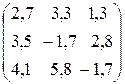

Диагонального преобладания элементов матрицы А нет. Значит, процессы итерации будут расходиться

А = D + В для матриц

D =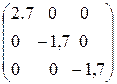

 В =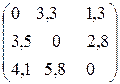

D^-1 =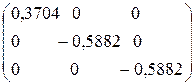

Метод простой итерации

х^{(к + 1)} = D^-1 ,

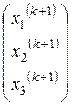=D^-1 *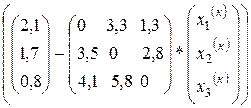

Обычно берут х⁽⁰⁾ = 0.

Затем вычисляют приближения

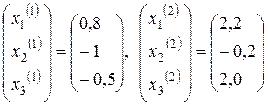
Уже видна расходимость, так как для данной системы

х^* ≈ (0,1; 0,3; 0,7).

Проверим метод Зейделя

А = L + D + C, где:

L =

Итерации имеют вид

+D) (

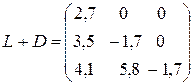
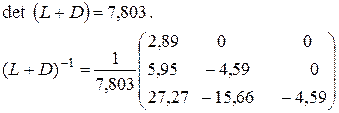
Нулевое приближение берём нулевым.

Вычисляется

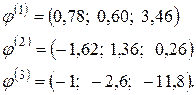
Процесс явно расходящийся.

Интерполирование и экстраполирование функции.

Задание 1.

Найти приближённое значение функции при данном значении аргумента с помощью интерполяционного многочлена Лагранжа.

х	у
1,375	5,04192
1,380	5,17744
1,385	5,32016
1,390	5,47069
1,395	5,62968
1,400	5,79788

х = 1,3832.

Решение.

Р₅ (х) = 5,04192 *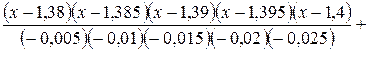

+

+

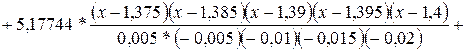
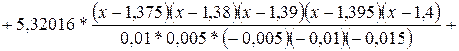
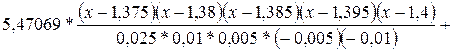
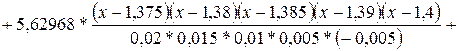
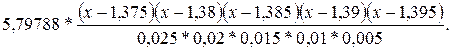
Знаменатели полученных дробей равны (по абсолютной величине):

15*25*10¹²

25*15*10¹⁰

3*25*10¹¹

25*30*10¹⁰

15*25*10¹⁰

15*25*10¹¹

При подстановке вместо х = 1,3832 получилось значение 6,28.

Интерполяция не состоялась. Видимо, не следует вычислять значения знаменателей, а оставить как есть, зато потом сокращать с множителями в числителе.

При втором способе вычислений получается F = (1,3832) = 5,26887.

Сказывается погрешность при использовании калькулятора.

Задание2.

Используя первую или вторую интерполяционные формулы Ньютона, вычислить значения функции при данных значениях аргумента. При составлении таблицы разностей контролировать вычисления.

х	у
1,415	0,888551
1,420	0,889599
1,425	0,890637
1,430	0,891667
1,435	0,892687
1,440	0,893698
1,445	0,894700
1,450	0,895693
1,455	0,896677
1,460	0,897653
1,465	0,898619

Значение аргумента
Х1	Х2	Х3	Х4
1,4161	1,4625	1,4135	1,470

Решение.

Вычисляем конечные разности.

0,001048
0,001038	-0,000010
0,001038	-0,000008	0,000002
0,001030	-0,000008	0	-0,000002
0,001011	-0,000019	-0,000011	-0,000011
0,001002	-0,000009	0,000010	0,000021
0,000993	-0,000009	0	-0,000010
0,000984	-0,000009	0	0
0,000976	-0,000008	0,000001	0,000001
0,000966	-0,000010	-0,000002	-0,000003
-0,00009
0,000032	0,000041
-0,000031	-0,000063	-0,000104
0,000010	0,000041	0,000104	0,000208
0,000001	-0,000009	-0,000050	-0,000150
-0,000004	-0,000005	0,000004	0,000054
-0,000358
0,000204	0,000562

Рассматриваем переменную:

t = x – 1,415 / 0,005.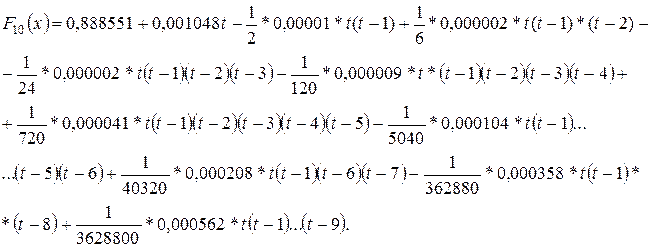

Для значения х₁ = 1,4161 будет t = 0,22.

В результате получается:

F₁₀ (х₁) = 0, 888551 + 0,00023056 + 0,0000010296 + … = 0,888782.

Для значения х₂ = 1,4625 будет t = 0,95

F₁₀ (х₂) = 0,898136.

Для значения х₃ = 1,4135 будет

t = -0,3;

F₁₀ (х₃) = 0,888227.

Для значения х₄ = 1,47 будет

t = 11;

F₁₀ (х₄) = 0,899585.

Видимо, по значениям F₁₀ (х₁), F₁₀ (х₂) проверяется правильность записи F₁₀ (х), а остальные значения уже решают задачу интерполяции.

Численное интегрирование.

1. Вычислить интеграл по формуле трапеций с тремя десятичными знаками;

2. Вычислить интеграл по формуле Симпсона при n = 8; оценить погрешность результата, составив таблицу конечных разностей;

3. Вычислить интеграл по формуле Гаусса.

1.

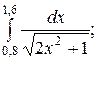
2. ;

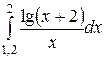3.

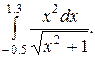
1. Решение.

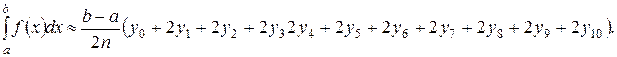
а = 0,8

в = 1,6

в – а = 0,8

n = 10

h = 0,08.

у₀ = 0,0662

у₁ = 0,627

у₂ = 0,593

у₃ = 0,562

у₄ = 0,534

у₅ = 0,508

у₆ = 0,484

у₇ = 0,461

у₈ = 0,441

у₉ = 0,422

у₁₀ = 0,404.

В результате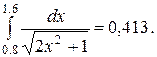

2. Решение.

а = 1,2

в = 2

в – а = 0,8

h = 0,8 / 8 = 0,1.

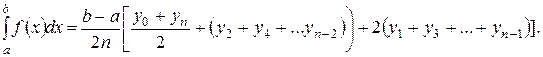
у₀ = 0,421

у₁ = 0,399

у₂ = 0,379

у₃ = 0,363

у₄ = 0,348

у₅ = 0,334

у₆ = 0,322

у₇ = 0,311

у₈ = 0,301.

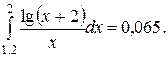
Погрешность определяется по формуле

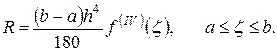
Производная четвёртого порядка имеет сложный вид. Погрешность оценить невозможно.

Учебник рекомендует взять шаг h / 2. Про использование конечных разностей в учебнике не написано.

3. Решение.

а = -0,5; в = 1,3.

х =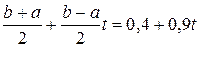

d_x = 0,9t

t =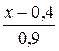

t₁ = -1

t₂ = 1.

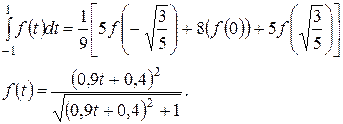
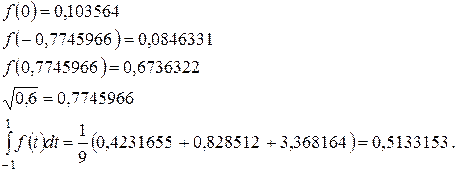
Про оценку погрешности в учебнике не сказано. Можно увеличивать число узлов, например, взять n = 5.

Численное решение обыкновенных дифференциальных уравнений

Используя метод Эйлера с уточнением, составить таблицу приближённых значений интеграла дифференциального уравнения у^/ = f (х,у), удовлетворяющего начальным условиям у(х₀) = у₀ на отрезке [a,b]; шаг h = 0,1. Все вычисления вести с четырьмя десятичными знаками.

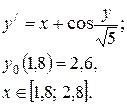
Решение.

В этом случае теория гарантирует хорошую сходимость.

х	у
1,8	2,6
1,9	2,8197
2,0	3,0402
2,1	3,2230
2,2	3,4460
2,3	3,6690
2,4	3,8920
2,5	4,1151
2,6	4,3385
2,7	4,5624
2,8	4,7871

Учебная литература

1.  Гладких Л.С. Курс вычислительной математики. Art – Avenue. –Новосибирск, 2004.

2.  Ращиков В.И., Рошаль А.С. Численные методы решения физических задач. – М.: Лань, 2005.