1. Теоретическая часть

Индексы, их виды. Агрегатные и средние индексы

Индекс (от лат. index – показатель, список, указатель) – статистический относительный показатель, характеризующий соотношение социально-экономических явлений во времени или в пространстве. То есть, любой показатель, выражающий сравнение двух величин между собой, можно называть индексом. В разговорной речи часто коэффициенты, разработанные статистической наукой для изучения отдельных социально-экономических явлений, также называют индексами. В статистике индекс – относительная величина, характеризующая изменение уровней сложных социально-экономических показателей во времени, в пространстве или по  сравнению с планом. Сложный показатель состоит из непосредственно несоизмеримых (несуммируемых элементов). Например, предприятие выпускает несколько видов продукции, но получить общий итог объема продукции путем суммирования количества различных ее видов в натуральном выражении нельзя.

В экономическом анализе индексы используются не только для сопоставления уровней изучаемого явления, но главным образом для определения экономической значимости причин, объясняющих абсолютное различие сравниваемых уровней.

Индексы вычисляются на высшей ступени статистического обобщения и опираются на результаты сводки и обработки данных статистического наблюдения.

С помощью индексных показателей  решаются следующие основные задачи[4,с . 188]:

1.     Характеристика общего изменения сложного экономического показателя и отдельных его элементов;

2.     Измерение влияния факторов на общую динамику сложного показателя, включая характеристику влияния изменения структуры явления.

Индексируемый признак – признак, изменение величины которого определяется. Название индексов обычно содержит указание на индексируемый признак. Например, если индексируемым признаком является объем произведенной продукции, выраженный в натуральных измерителях, то название индекса определяется как «Индекс физического объема произведенной продукции». При построении индексов, также как при построении средних величин, используются признаки-веса[3,с . 17].

Взаимосвязь между индексами выражается таким же соотношением, как и взаимосвязь между признаками, на основе которых строятся индексы. Например, если размер дохода за месяц одного жителя региона N умножить на число человек, живущих в этом регионе, то получим общий доход, получаемый всеми жителями данного региона, – именно так будет выглядеть взаимосвязь между этими признаками. Следовательно, и между индексами, отражающими изменение указанных признаков, будет такая же взаимосвязь: произведение индекса дохода на душу населения региона и индекса численности жителей региона даст индекс общего дохода всех жителей региона. Однако, следует внимательно относиться к данному правилу, т.к. взаимосвязь между признаками может выражаться суммой или разностью. Индексы, являясь относительным показателями, всегда взаимосвязаны между собой произведением или отношением.

Взаимосвязь между индексами выражается таким же соотношением, как и взаимосвязь между признаками, на основе которых строятся индексы. Например, если размер дохода за месяц одного жителя региона N умножить на число человек, живущих в этом регионе, то получим общий доход, получаемый всеми жителями данного региона, – именно так будет выглядеть взаимосвязь между этими признаками. Следовательно, и между индексами, отражающими изменение указанных признаков, будет такая же взаимосвязь: произведение индекса дохода на душу населения региона и индекса численности жителей региона даст индекс общего дохода всех жителей региона. Однако, следует внимательно относиться к данному правилу, т.к. взаимосвязь между признаками может выражаться суммой или разностью. Индексы, являясь относительным показателями, всегда взаимосвязаны между собой произведением или отношением.

Если известно, что изучаемое явление неоднородно и сравнение уровней можно провести только после приведения их к общей мере, экономический анализ выполняют посредством так называемых общих индексов. Индекс становится общим, когда в расчетной формуле показывается неоднородность изучаемой совокупности. Примером неоднородной совокупности является общая масса проданных товаров всех или нескольких видов. Тогда сумму выручки можно записать в виде агрегата (суммы произведений взвешивающего показателя на объемный), например[2, с. 190]:

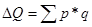
Отношение агрегатов, построенных для разных условий, дает общий индекс показателя в агрегатной форме. Так, например, получают индекс общего объема товарооборота в агрегатной форме:

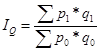
При анализе прироста общего объема товарооборота этот прирост также объясняется изменением уровня цен и количества проданных товаров.

Влияние на прирост товарооборота общего изменения цен выражается агрегатным индексом цен I_p, который в предположении первичности изменения количественного показателя (q) и вторичности – качественного (р) имеет вид

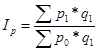
Влияние на прирост товарооборота изменения количества проданных товаров отражается агрегатным индексом физического объема I_q , который строится также в предположении первичности изменения количественных показателей (q) и вторичности влияния качественных (р):

В форме мультипликативной индексной модели динамика товарооборота будет выражаться соотношениями

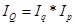или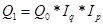 

где ;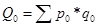

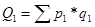
Если принимается предположение об очередности влияния факторов – сначала q, а затем р, то общий прирост товарооборота будет распределяться по факторам следующим образом:

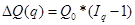
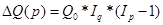
Если же принимается предположение об обратной последовательности влияния факторов – сначала р, затем q, то меняются и формулы разложения прироста и формулы расчета индексов I_q и I_p . Тогда

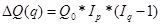
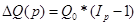
где

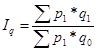
Примером мультипликативной индексной модели с большим числом факторов является изменение общей суммы материальных затрат на производство продукции. Сумма затрат зависит от количества выпущенной продукции (индекс I_q), удельных расходов (норм) материала на единицу продукции (индекс I_n) и цены на материалы (индекс I_p). Прирост общей суммы затрат распределяется следующим образом:

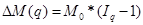
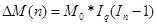
где 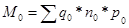, а величины индексов таковы:

Ø индекс увеличения суммы затрат в связи с изменением объемов производства продукции (индекс физического объема)

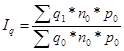
Ø индекс изменения суммы затрат за счет изменения удельных расходов материала (индекс удельных расходов)

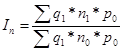
Ø индекс изменения общей суммы затрат, объясняемого изменением цен на материалы (индекс цен на материалы)

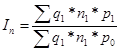
Аналогичным образом находят общие агрегатные индексы и по многим другим экономическим показателям. Нетрудно заметить, что используемые в приведенных формулах индексы I_q, I_Т, I_ф получаются по методу индекса физического объема, а индексы I_z, I_f, I_W, I_H – по методу индекса цен. Таким образом, рассмотренная выше методика распределения общего прироста товарооборота полностью приложима к анализу прироста продукции, изменения общих затрат на производство, изменения общего фонда оплаты труда и т.д.

Если необходимо охарактеризовать изменение качественных показателей, то находятся средние величины этих показателей, а на их основе определяется индекс переменного состава.

,

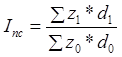где z1, z0 – себестоимость продукции на отдельных предприятиях (цехах) соответственно в отчётном и базисном периоде, тыс. руб./т.

d1, d0 – удельный вес, доля данного предприятия (цеха) в общем объёме производства соответственно в отчётном и базисном периоде.

Изменение средней себестоимости зависит от изменения себестоимости данного вида продукции на отдельных предприятиях (цехах) и от изменения доли, удельного веса данного предприятия (цеха) в общем объёме производства.

Чтобы определить влияние каждого из факторов по отдельности строят соответствующие индексы:

1. Индекс фиксированного состава. Он определяет влияние изменения себестоимости данного вида продукции на отдельных предприятиях (цехах) на общее изменение средней себестоимости.

,

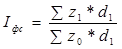где z1, z0 – себестоимость продукции на отдельных предприятиях (цехах) соответственно в отчётном и базисном периоде, тыс. руб./т.

d1 – удельный вес, доля данного предприятия (цеха) в общем объёме производства в отчётном периоде.

2. Индекс структурных сдвигов. Он определяет влияние изменения доли, удельного веса данного предприятия (цеха) в общем объёме производства на общее изменение средней себестоимости.

,

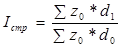где z0 – себестоимость продукции на отдельных предприятиях (цехах) соответственно в базисном периоде, тыс. руб./т.

d1, d0 – удельный вес, доля данного цеха (участка) в общем объёме производства соответственно в отчётном и базисном периоде.

Данные индексы образуют систему взаимосвязанных индексов, т.е.

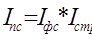
Удельный вес, доля данного предприятия (цеха) в общем объёме производства определяется по следующей формуле:

,

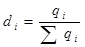где qi – объем производства i-ым цехом (предприятием), тыс.

2. Задача

УСЛОВИЕ ЗАДАЧИ

         По данному ряду построить  теоретический ряд. Оценить близость фактического и теоретического распределения с помощью критерия Пирсона. Теоретический и графический ряд изобразить графически.

РЕШЕНИЕ

Таблица 1

Исходные данные задачи

Определим средние значения интервалов

Таблица 2

1)    Принимаем величину стажа работников за переменную х, а величину количества работников за переменную y. Тогда значения х_ср и y_ср определяем по формулам (1) и (2):

х_ср = (Σ x_i) / n,                      (1)

y_ср = (Σ y_i) / n,                      (2)

где    n = 5,

         i = 1…5

Тогда, х_ср = 90 : 6 = 15

           y_{ср =}  86 : 6 = 14,3

2)    Дальнейшие результаты расчета представляем в виде таблицы 3

Таблица 3

Σ(x_i - х_ср)² = 317,25

Σ(y_i - y_ср)² = 114,45

Σ(x_i - х_ср)( y_i - y_ср) = 9,65

3)    Теснота связи между показателями измеряется критерием Пирсона, который исчисляется по формуле (3):

V = δ²_xy / δ_x · δ_y,                                      (3)

где    V – коэффициент корреляции,

δ_x = [Σ(x_i - х_ср)²/ n]^1\2,                   (4)

δ_y = [Σ(y_i - y_ср)²/ n]^1\2,                   (5)

δ²_xy = 1/n ∑ (x_i - х_ср)( y_i - y_ср),              (6)

Подставляя имеющиеся значения  в формулы (4),(5),(6),получаем:

δ_x = (317,25/6)^1/2 = (52,9)^1/2 = 7,3

δ_y = (114,45/6)^1/2 = (19,075)^1/2 =4,4

δ²_xy = 9,65/6 = 1,6

Тогда, значение критерия Пирсона равно:

V = 1,6/ (7,3 *4,4) ≈ 0,05

4)    Считая формулу связи между показателями линейной (y = a₀ + a₁x), определим зависимость показателем. Для этого решается система нормальных уравнений:

na₀ + a₁∑x_i = ∑y_i,                          (7)

a₀∑x_i + a₁∑x_i² = ∑ x_i y_i,                      (8)

Величины ∑x_i² и ∑ x_i y_i представлены в таблице 3.

Таблица 3

         Значение a₀ определяем из формулы (7):

6 a₀ + 90 a₁ = 86,

90 a₀ + 1787,5 a₁ = 1190

a₀ = (86 – 90  a₁)/ 6,

или a₀ = 14,3 – 15 a₁

         Подставляя найденное значение a₀  в формулу (8), находим значение a₁:

90 (14,3 – 15 a₁) + 1787,5 a₁ = 1190

1287 – 1350 a₁ + 1787,5 a₁ = 1190

437,5 a₁ = -97

a₁ =  - 0,22

Тогда, a₀ = 14,3 - 15 * - 0,22 = 11

         Итак, уравнение регрессии в окончательном виде имеет следующий вид:

y = 11 -  0,22 · x

Таблица 4

Фактические и теоретические значения

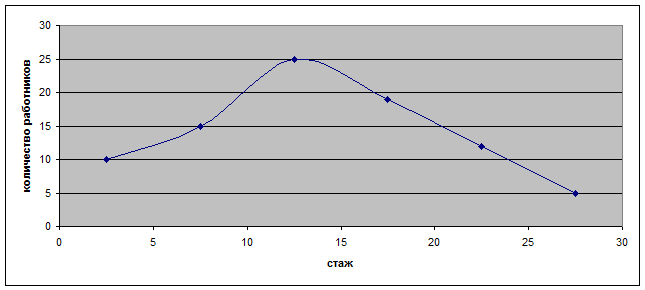
Рис. 1. Фактический тренд зависимости количества работников от стажа

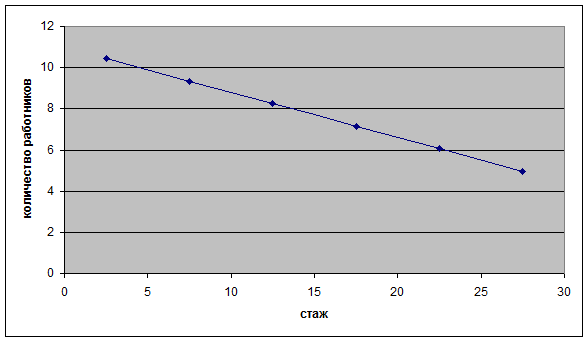
Рис. 2. Теоретический тренд зависимости количества работников от стажа