Задача 5.
Результаты роста Х (см) и
веса Y (кг) 86 школьников приведены в следующей таблице 1:
Таблица 1.
Исходные
данные для задачи
|
Y
Х
|
22,5 – 25,5
|
28,5 – 28,5
|
28,5 – 31,5
|
31,5 – 34,5
|
34,5 – 37,5
|
Всего
|
|
117,5 – 122,5
|
3
|
5
|
–
|
–
|
–
|
8
|
|
122,5 – 127,5
|
–
|
4
|
8
|
3
|
–
|
15
|
|
127,5 – 132,5
|
–
|
3
|
7
|
7
|
–
|
17
|
|
132,5 – 137,5
|
–
|
3
|
8
|
9
|
4
|
24
|
|
137,5 – 142,5
|
–
|
–
|
3
|
6
|
4
|
13
|
|
142,5 – 147,5
|
–
|
–
|
–
|
3
|
3
|
6
|
|
147,5 – 152,5
|
–
|
–
|
–
|
–
|
3
|
3
|
|
Всего
|
3
|
15
|
26
|
28
|
14
|
86
|
Предполагая, что между X и Y существует линейная корреляционная
зависимость, требуется:
А) Вычислить коэффициент
корреляции и проанализировать степень тесноты и направление связи;
Б) Составить уравнения
прямых регрессии и построить их графики;
В) Используя
соответствующее уравнение регрессии, определить рост школьника при весе в 45 кг.
Решение:
Так как в задаче нет
дискретных данных показателей, а только их интервальные значения, то и расчет
будет вестись, исходя из среднего интервального значения. Для этого составим
дополнительную таблицу 2.
Таблица2.
Вспомогательная
таблица данных
|
Y’
Х’
|
(22,5 + 25,5)/2 = 24
|
27
|
30
|
33
|
36
|
Всего
|
|
(117,5 + 122,5)/2 = 120
|
3
|
5
|
–
|
–
|
–
|
8
|
|
125
|
–
|
4
|
8
|
3
|
–
|
15
|
|
130
|
–
|
3
|
7
|
7
|
–
|
17
|
|
135
|
–
|
3
|
8
|
9
|
4
|
24
|
|
140
|
–
|
–
|
3
|
6
|
4
|
13
|
|
145
|
–
|
–
|
–
|
3
|
3
|
6
|
|
150
|
–
|
–
|
–
|
–
|
3
|
3
|
|
Всего
|
3
|
15
|
26
|
28
|
14
|
86
|
Х’, Y’ – средние значения показателей.
1.
Коэффициент корреляции высчитывается по следующим формулам
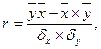где r – парный коэффициент корреляции,
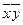- среднее произведение
факторного и результативного признаков,
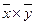-произведение средних
размеров факторного и результативного признаков,
, 
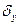- среднее
квадратическое отклонение факторного и результативного признаков. Причем
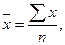
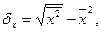
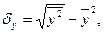
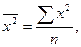
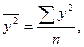
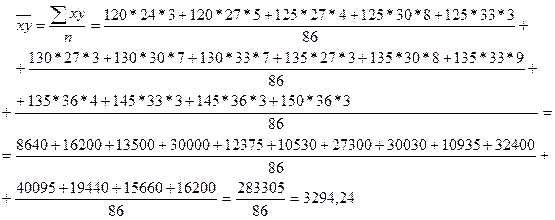
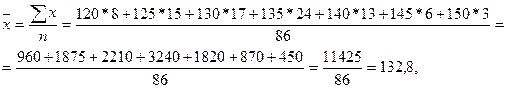
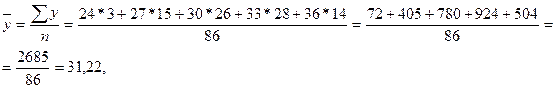
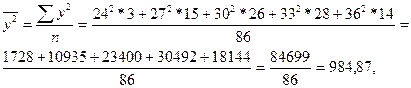
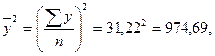
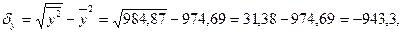
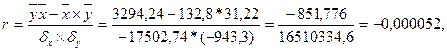
Коэффициент корреляции r = - 5,2*10-6, коэффициент
детерминации d =
27,04*10-12.
Это свидетельствует о слабой зависимости между
признаками. Влияние роста школьника на его вес составляет 27,04*10-12
% (d = 27,04*10-12).
Связь обратная, так как коэффициент корреляции отрицательный.
2.
При линейной форме связи используется уравнение прямой Y = A + Bx, где у – теоретический уровень результативного признака (вес
школьников), а – начало отсчета, х – факторный признак (рост школьников), в –
коэффициент регрессии, показывающий среднее изменение результативного признака
при изменении факторного признака на единицу.
При
линейной форме связи система имеет вид:
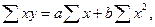где n – численность совокупности (в данном
случае n = 86).
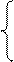2685 =
86a + 11425b;
283305 = 11425a + 1522725b.
Система
решается методом подстановки.
а = (2685
– 11425b)/86 = 31,22 –
132,8b
11425*(31,22
– 132,8b) = 283305
356688,5
– 1517240b = 283305
b = (356688,5 –
283305)/1517240 = 0,05.
a = 31,22 – 132,8*0,05 = 24,6.
Тогда
уравнение регрессии равно
Y = 24,6 + 0,05x.
Построим
его график
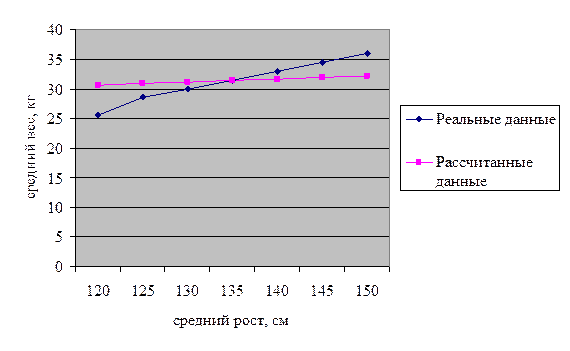
3.
Исходя из полученного уравнения регрессии выразим Х.
Х = (Y – 24,6)/0,05.
Отсюда
находим, что при весе в 45 кг
школьник будет иметь рост:
Х = (45 –
24,6)/0,05 = 165 см.
Список используемой литературы
1.
Барнгольц С.Б., Мельник М.В. Методология экономического
анализа деятельности хозяйствующего субъекта: Учеб. пособие. – М.: Финансы и
статистика, 2003.
2.
Башет К.В. Статистика коммерческой деятельности. – М: Финансы и статистика. 1996 г.
3.
Гологенов В.А. Статистическое наблюдение как один из
методов статистики//Вопросы статистики 1997 г. №2, №4, №5.
4.
Невзоров К.Л. Статистика как наука//Вопросы статистики 1996 г. №1, №11.
5.
Елесеева М.А. Общая теория статистики.– М.: Статистика,
1988.
6.
Елисеева И.И., Юзбашев М.М. Общая теория статистики. –
М.: «Инфра-М», 1999.
7.
Ефимова М.Р. Общая теория статистики. – М.:
«Мира-люкс», 2002.
8.
Савицкая Г.В. Экономический анализ: Учеб./Г.В.Савицкая.
– 8-е изд., перераб. – М.: Новое знание, 2003.
9.
Общая теория статистики/Под ред. Спирина И.А.. – М.:
«Инфра-М», 2001.
Харченко
Л.П. Статистика. – М: ИНФРА, 1997.