Министерство образования и науки РФ
Федеральное агентство по образованию
Государственное общеобразовательное
учреждение высшего
профессионального образования
Всероссийский заочный
финансово-экономический институт
Филиал в г. Туле
К О Н Т Р О Л Ь Н А Я Р А Б О
Т А
По дисциплине «Финансовая математика»
Вариант №8
Выполнил: студент 4 курса
факультета финансово-кредитного
специальности ФиК
группа: вечерняя
Руководитель: Арсеньев Ю.Н.
Тула
2007г.
ОГЛАВЛЕНИЕ
1. Задание 1……………………………….…………………………………....3
2.
Задание 2……………………………….…………………………………...14
3.
Задание 3……………………………………….…………………………...21
Список использованной литературы……..…………..………………………24
Задание 1.
Приведены поквартальные
данные о кредитах от коммерческого банка на жилищное строительство (в условных
единицах) за 4 года (всего 16 кварталов, первая строка соответствует первому
кварталу первого года):
Таблица 1. Исходные значения заданного временного ряда
|
Т
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
|
Y(t)
|
39
|
50
|
59
|
38
|
42
|
54
|
66
|
40
|
45
|
58
|
69
|
42
|
50
|
62
|
74
|
46
|
Требуется:
1) Построить адаптивную
мультипликативную модель Хольта-Уинтерса с учетом сезонного фактора, приняв
параметры сглаживания α1=0,3; α2=0,6; α3=0,3.
2) Оценить точность построенной модели с
использованием средней относительной ошибки аппроксимации.
3) Оценить адекватность построенной
модели на основе исследования:
- случайности остаточной компоненты по
критерию пиков;
- независимости уровней ряда остатков по d-критерию (критические значения d1=1,10 и d2=1,37) и по первому коэффициенту
автокорреляции при критическом значении r1=0,32;
- нормальности
распределения остаточной компоненты по R/S-критерию с критическими значениями
от 3 до 4,21.
4) Построить точечный прогноз на 4 шага
вперед, т.е. на 1 год.
5) Отразить на графике фактические,
расчетные и прогнозные данные.
Решение:
1. Построение модели
Хольта-Уинтерса
Для оценки начальных
значений 
и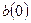 
применим линейную модель
с первыми восьми значениями заданного временного ряда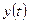 
(Таблица 2).
Линейная модель имеет
вид: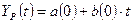 
. Оценим коэффициенты линейной модели и 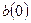с помощью метода
наименьших квадратов (МНК).
Таблица 2. Расчёт коэффициентов линейной модели
|
|
|
|
|
|
|
|
|
|
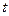
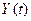
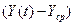
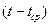
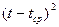
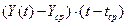
1
|
39
|
-9,5
|
-3,5
|
33,25
|
12,25
|
|
|
2
|
50
|
1,5
|
-2,5
|
-3,75
|
6,25
|
|
|
3
|
59
|
10,5
|
-1,5
|
-15,75
|
2,25
|
|
|
4
|
38
|
-10,5
|
-0,5
|
5,25
|
0,25
|
|
|
5
|
42
|
-6,5
|
0,5
|
-3,25
|
0,25
|
|
|
6
|
54
|
5,5
|
1,5
|
8,25
|
2,25
|
|
|
7
|
66
|
17,5
|
2,5
|
43,75
|
6,25
|
|
|
8
|
40
|
-8,5
|
3,5
|
-29,75
|
12,25
|
|
Сумма
|
36
|
388
|
|
|
38
|
42
|
|
Среднее
значение
|
4,5
|
48,5
|
|
|
|
|
Определим значения
коэффициентов нашей линейной модели по формулам:
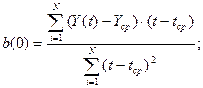
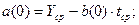
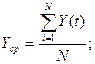
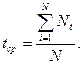
Подставив исходные
данные, получим:
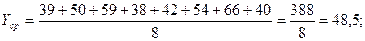
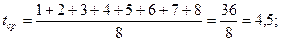
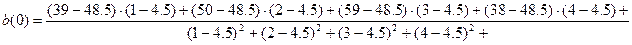
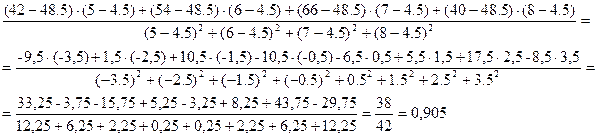
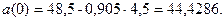
Линейная модель с учетом
полученных коэффициентов имеет вид:
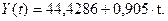
Из этого уравнения
находим расчётные значения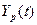 
и сопоставляем их с
фактическими значениями заданного временного ряда (Таблица 3).
Таблица 3. Значения заданного временного ряда и расчетной модели
|
Т
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
Y(t)
|
39
|
50
|
59
|
38
|
42
|
54
|
66
|
40
|
|
Yр(t)
|
45,3336
|
46,2386
|
47,1436
|
48,0486
|
48,9536
|
49,8586
|
50,7636
|
51,6686
|
Оценим приближенные
значения коэффициентов сезонности I – IV кварталов F(-3), F(-2), F(-1) и F(0) для года, предшествующего году,
по которому имеются данные. В результате расчёта получим следующие данные:
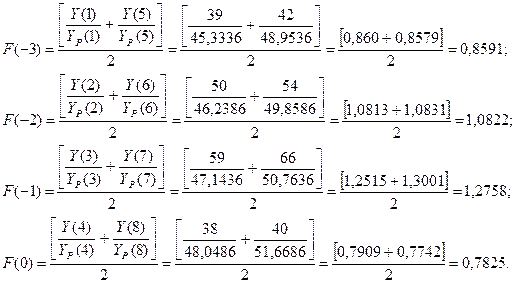
Адаптивная
мультипликативная модель Хольта-Уинтерса имеет вид:
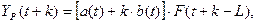
Где k – период упреждения;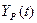 
- расчетное
значение показателя для t-го периода; a(t), b(t) и F(t) – коэффициенты модели;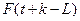 
- значение коэффициента сезонности
того периода, для которого рассчитывается показатель; L – период сезонности (для квартальных данных L=4).
Уточнение (адаптация к
новому значению параметра времени t) коэффициентов модели производятся
по формулам:
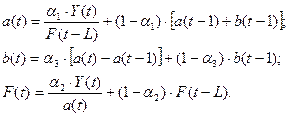
Значения параметров сглаживания,
согласно заданию, таковы:
Тогда для момента времени
t=0, k=1 имеем:
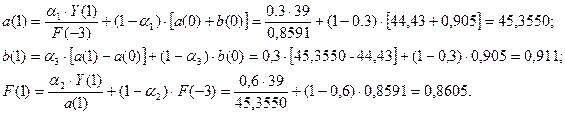
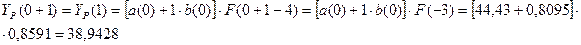
При моменте времени t=1 имеем:
Для t=1, k=1 имее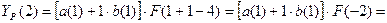м: 
Для момента времени t=2 имеем:
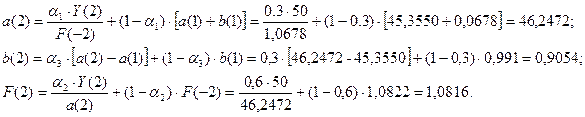
Для t=2, k=1 имеем: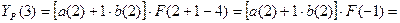 
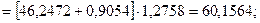
Для момента времени t=3 имеем:
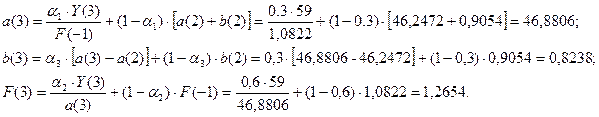
Для t=3, k=1 имеем: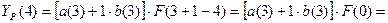 
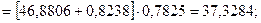
Для момента времени t=4 имеем:
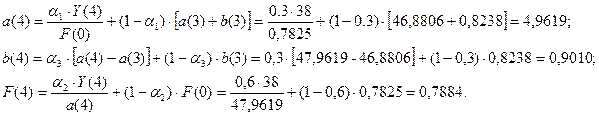
Для t=4, k=1 имеем: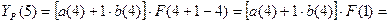 
Для момента времени t=5 имеем:
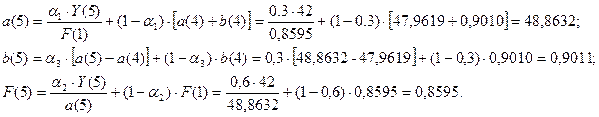
Для t=5, k=1 имеем: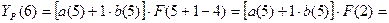 
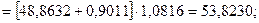
Для момента времени t=6 имеем:
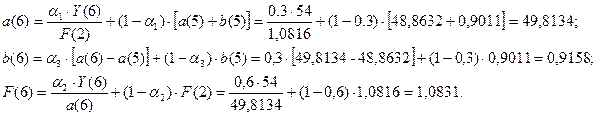
Для t=6, k=1 имеем: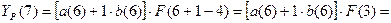 
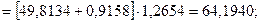
Для момента времени t=7 имеем:
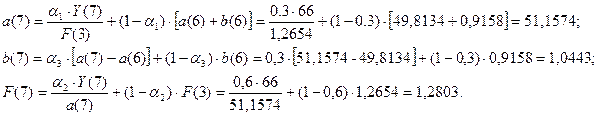
Для t=7, k=1 имеем: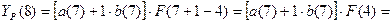 
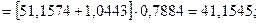
Для момента времени t=8 имеем:
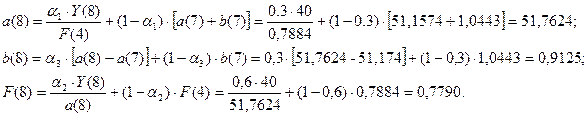
Для t=8, k=1 имеем: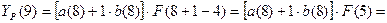 
Для момента времени t=9 имеем:
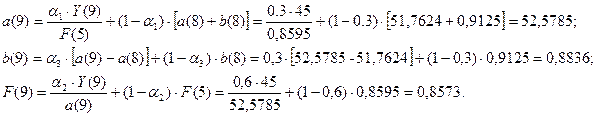
Для t=9, k=1 имеем: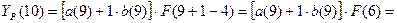 
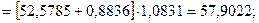
Для момента времени t=10 имеем:
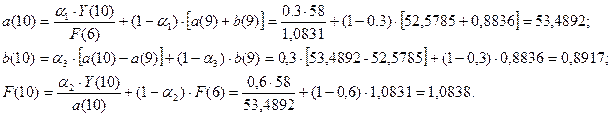
Для t=10, k=1 имеем: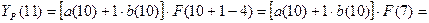 
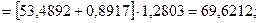
Для момента времени t=11 имеем:
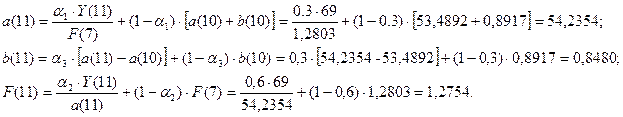
Для t=11, k=1 имеем: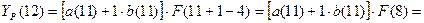 
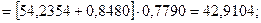
Для момента времени t=12 имеем:
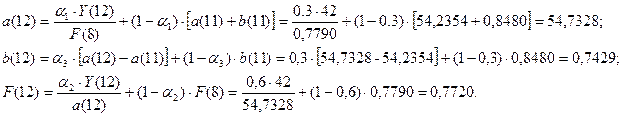Для t=12, k=1 имеем: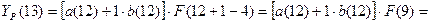 
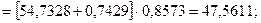
Для момента времени t=13 имеем:
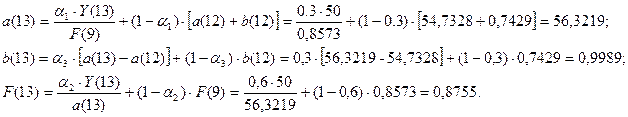
Для t=13, k=1 имеем: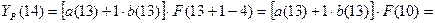 
Для момента времени t=14 имеем:
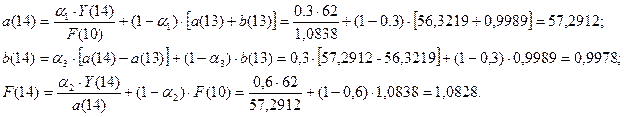
Для t=14, k=1 имеем: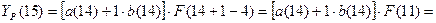 
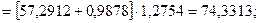
Для момента времени t=15 имеем:
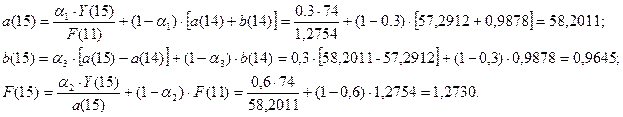
Для t=15, k=1 имеем: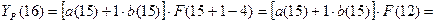 
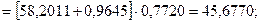
Для момента времени t=16 имеем:
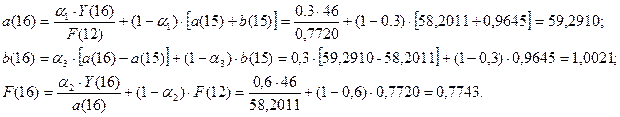
Занесем полученные данные
модели Хольта-Уинтерса в таблицу 4.
2. Проверка точности модели
Оценим точность полученной модели по средней
относительной ошибке аппроксимации:
Таблица 4. Расчётные данные по модели Хольта-Уинтерса
|
|
|
|
|
|
|
|
|
|
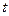
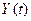
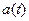
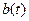
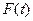
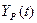
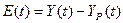
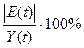
0
|
|
44,4300
|
0,9050
|
0,7825
|
|
|
|
|
1
|
39
|
45,3550
|
0,9110
|
0,8595
|
38,9428
|
0,0572
|
0,1468
|
|
2
|
50
|
46,2472
|
0,9054
|
1,0816
|
50,0678
|
-0,0678
|
0,1357
|
|
3
|
59
|
46,8806
|
0,8238
|
1,2654
|
60,1564
|
-1,1564
|
1,9600
|
|
4
|
38
|
47,9619
|
0,9010
|
0,7884
|
37,3284
|
0,6716
|
1,7675
|
|
5
|
42
|
48,8632
|
0,9011
|
0,8595
|
41,9991
|
0,0009
|
0,0021
|
|
6
|
54
|
49,8134
|
0,9158
|
1,0831
|
53,8230
|
0,1770
|
0,3278
|
|
7
|
66
|
51,1574
|
1,0443
|
1,2803
|
64,1940
|
1,8060
|
2,7364
|
|
8
|
40
|
51,7624
|
0,9125
|
0,7790
|
41,1545
|
-1,1545
|
2,8863
|
|
9
|
45
|
52,5785
|
0,8836
|
0,8573
|
45,2760
|
-0,2760
|
0,6134
|
|
10
|
58
|
53,4892
|
0,8917
|
1,0838
|
57,9022
|
0,0978
|
0,1687
|
|
11
|
69
|
54,2354
|
0,8480
|
1,2754
|
69,6212
|
-0,6212
|
0,9003
|
|
12
|
42
|
54,7328
|
0,7429
|
0,7720
|
42,9104
|
-0,9104
|
2,1676
|
|
13
|
50
|
56,3291
|
0,9989
|
0,8755
|
47,5611
|
2,4389
|
4,8777
|
|
14
|
62
|
57,2912
|
0,9878
|
1,0828
|
62,1332
|
-0,1332
|
0,2148
|
|
15
|
74
|
58,2011
|
0,9645
|
1,2730
|
74,3313
|
-0,3313
|
0,4478
|
|
16
|
46
|
59,2910
|
1,0021
|
0,7743
|
45,6770
|
0,3230
|
0,7021
|
|
Сумма
|
|
|
|
|
|
0,92
|
20,0549
|
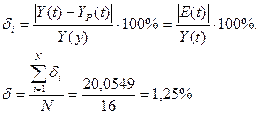
Так как средняя
относительная ошибка аппроксимации меньше 5%, то условие точности выполнено.
3. Проверка условий адекватности
Оценим адекватность построенной модели. Для
оценки адекватности модели исследуемому процессу нужно, чтобы ряд остатков E(t) обладал свойствами случайности,
независимости последовательных уровней, нормальности распределения.
Проверку случайностей
уровней остаточной компоненты проводим на основе критерия поворотных точек,
сведя промежуточные данные расчётов в
таблице 5.
Таблица 5. Промежуточные расчёты для оценки
адекватности модели
|
|
|
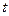
Точки
поворота
|
|
|
|
|
|
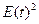
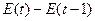
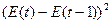
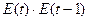
1
|
0,0572
|
-
|
0,0033
|
-
|
-
|
-
|
|
2
|
-0,0678
|
0
|
0,0046
|
-0,1251
|
0,0156
|
-0,0039
|
|
3
|
-1,1564
|
1
|
1,3373
|
-1,0886
|
1,1850
|
0,0784
|
|
4
|
0,6716
|
1
|
0,4511
|
1,8281
|
3,3418
|
-0,7767
|
|
5
|
0,0009
|
1
|
0,0000
|
-0,6708
|
0,4499
|
0,0006
|
|
6
|
0,1770
|
0
|
0,0313
|
0,1761
|
0,0310
|
0,0002
|
|
7
|
1,8060
|
1
|
3,2617
|
1,6290
|
2,6536
|
0,3197
|
|
8
|
-1,1545
|
1
|
1,3329
|
-2,9605
|
8,7648
|
-2,0851
|
|
9
|
-0,2760
|
0
|
0,0762
|
0,8785
|
0,7717
|
0,3187
|
|
10
|
0,0978
|
1
|
0,0096
|
0,3739
|
0,1398
|
-0,0270
|
|
11
|
-0,6212
|
0
|
0,3859
|
-0,7191
|
0,5170
|
-0,0608
|
|
12
|
-0,9104
|
1
|
0,8288
|
-0,2891
|
0,0836
|
0,5656
|
|
13
|
2,4389
|
1
|
5,9481
|
3,3493
|
11,2175
|
-2,2203
|
|
14
|
-0,1332
|
0
|
0,0177
|
-2,5720
|
6,6154
|
-0,3248
|
|
15
|
-0,3313
|
1
|
0,1098
|
-0,1982
|
0,0393
|
0,0441
|
|
16
|
0,3230
|
-
|
0,1043
|
0,6543
|
0,4281
|
-0,1070
|
|
Сумма
|
0,92
|
9
|
13,9026
|
|
36,2543
|
-4,2783
|
Общее число поворотных
точек р в данной задаче (см. таблицу
5) равно 9.
Рассчитаем значение q:
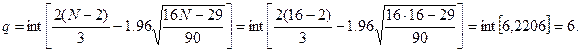
Так как p > q, то условие
случайностей ряда остатков выполняется, следовательно, модель по этому критерию адекватна.
Проверку независимости
уровней ряда остатков (отсутствие автокорреляции). Проверку проведем двумя
методами:
1. По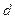 
-критерию Дарбина-Уотсона;
2. По первому
коэффициенту автокорреляции r(1).
Рассчитаем 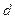-критерий Дарбина-Уотсона:
1. 
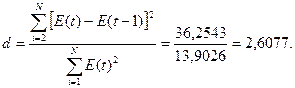
Расчётное значение
находится в интервале от 2 до 4, что свидетельствует об отрицательной связи. В
этом случае его надо преобразовать по формуле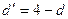 
и в дальнейшем
использовать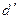 
.
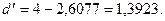
Так как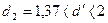 
, то уровни ряда остатков являются независимыми. Следовательно,
модель адекватна.
2.
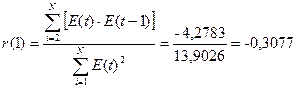
Так как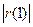 
< 
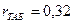, то уровни ряда остатков независимы.
Проверку соответствия
ряда остатков нормальному распределению выполним по R/S-критерию с
критическими значениями от 3 до 4,21:
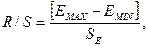где
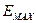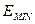- максимальное значение уровней ряда
остатков ,
- минимальное значение уровней ряда
остатков ,
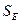- среднее квадратическое отклонение.
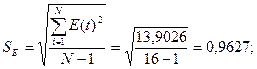
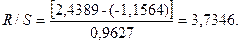
Так как полученное
значение входит в интервал от 3 до 4,21,
то уровни ряда подчиняются нормальному распределению, следовательно,
модель по этому критерию адекватна.
Таким образом, не все
условия адекватности выполнены. Следовательно, нельзя говорить об
удовлетворительном качестве модели и возможности проведения прогноза показателя
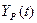на четыре квартала
вперед.
Построим точечный прогноз
на 4 шага вперед:
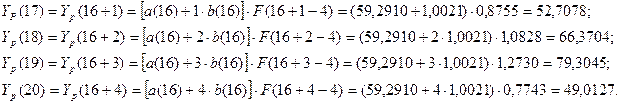
Отобразим на графике
фактические, расчётные и прогнозные данные. Из графика видно, что расчётные
данные хорошо согласуются с фактическими значениями, что говорит от
удовлетворительном качестве прогноза.
Задание 2.
Даны цены (открытия,
максимальная, минимальная и закрытия) за 10 дней. Интервал сглаживания принять
равным пяти дням. Рассчитать:
- экспоненциальную скользящую
среднюю;
- момент;
- скорость изменения цен;
- индекс относительной силы;
- %R, %K, %D.
Расчеты проводить для
всех дней, для которых эти расчеты можно выполнить на основании имеющихся
данных.
Таблица 6. Исходные данные
|
Дни
|
Цены
|
|
Макс.
|
Мин.
|
Закр.
|
|
1
|
595
|
580
|
585
|
|
2
|
579
|
568
|
570
|
|
3
|
583
|
571
|
578
|
|
4
|
587
|
577
|
585
|
|
5
|
586
|
578
|
582
|
|
6
|
594
|
585
|
587
|
|
7
|
585
|
563
|
565
|
|
8
|
579
|
541
|
579
|
|
9
|
599
|
565
|
599
|
|
10
|
625
|
591
|
618
|
Решение:
Рассчитаем
экспоненциальную скользящую среднюю по формуле:
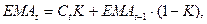
где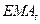 
- значение экспоненциальной скользящей
средней текущего дня t; 
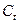- цена
закрытия t- го дня,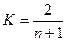 
- коэффициент.
Интервал сглаживания n=5.
Тогда коэффициент К будет равен: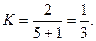 
Вычислим простую среднюю
для первых 5 дней. Получим следующее:
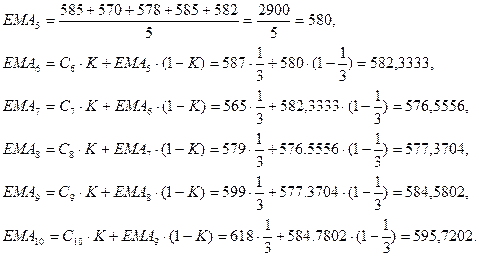
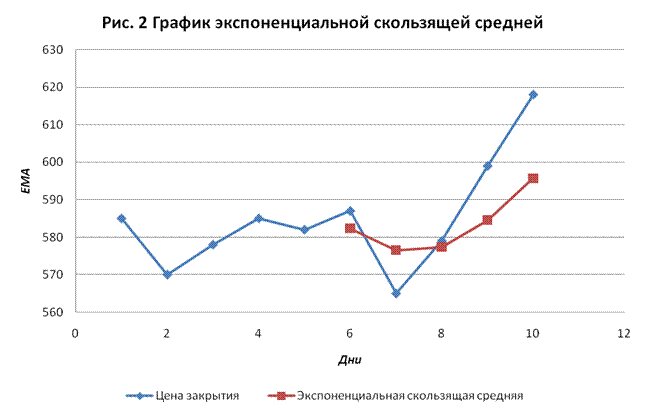
Экспоненциальная
скользящая средняя является индикатором тренда. Из графика (Рис. 2) видно, что ЕМА пересекает ценовой график в районе
6-8 дня и идет над графиком цен что является сигналом к продаже.
Рассчитаем момент по
следующей формуле:
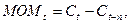
где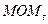 
- значение
момента текущего дня t,
- цена
закрытия t-го дня, 
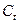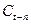- цена
закрытия n дней назад. В итоге получим
следующие значения момента:
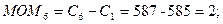
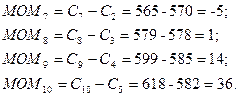
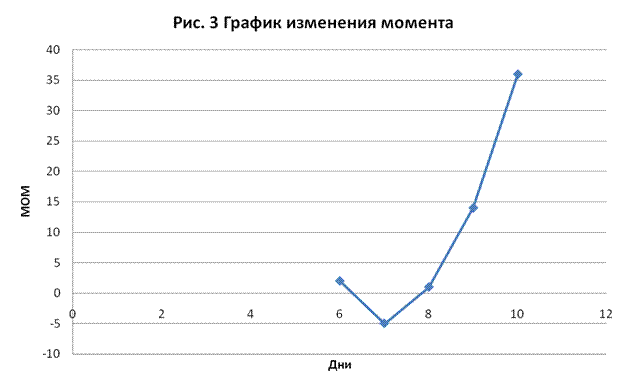
График момента (Рис. 3)
пересекает нулевую линию в районе 6-8 дня, что является сигналом к продаже.
Рассчитаем скорость
изменения цен по следующей формуле:
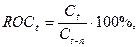
где 
- значение скорости изменения цен
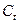текущего дня t, - цена закрытия t-го дня, 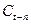- цена
закрытия n дней назад.
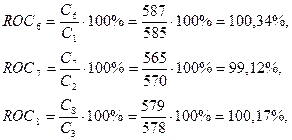
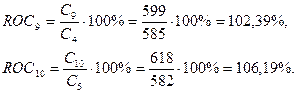
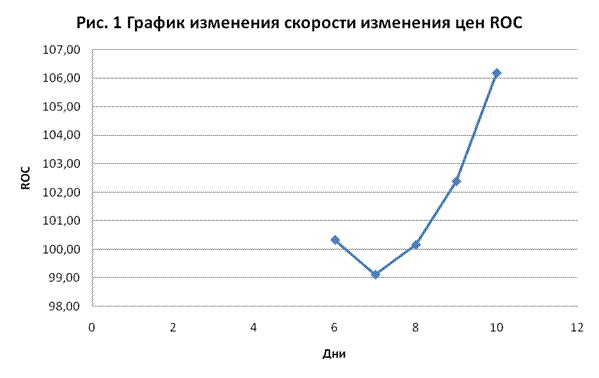
График ROC (Рис. 4) пересекает уровень 100% в районе 6-8 дня
сверху вниз, что является сигналом к продаже.
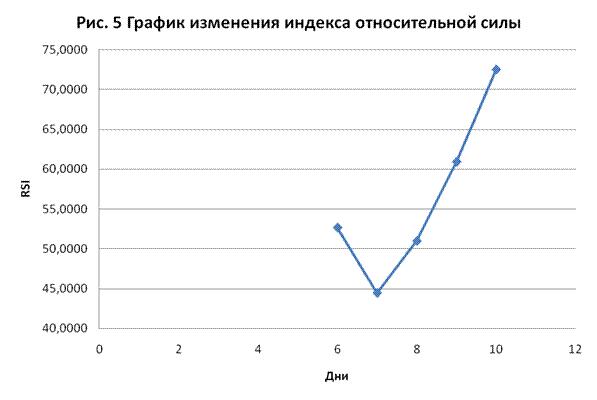
Рассчитаем индекс
относительной силы по следующей формуле:
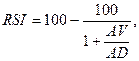
где AV (AD) – сумма приростов (убыли) конечных
цен за n дней.
Для этого заполним
таблицу.
|
Дни
|
Цена закрытия
|
Повышение цены
|
Понижение цены
|
Сумма повышений
|
Сумма понижений
|
RSI
|
|
Гр.1
|
Гр.2
|
Гр.3
|
Гр.4
|
Гр.5
|
Гр.6
|
Гр.7
|
|
1
|
585
|
|
|
|
|
|
|
2
|
570
|
|
15
|
|
|
|
|
3
|
578
|
8
|
|
|
|
|
|
4
|
585
|
7
|
|
|
|
|
|
5
|
582
|
|
3
|
|
|
|
|
6
|
587
|
5
|
|
20
|
18
|
52,6316
|
|
7
|
565
|
|
22
|
20
|
25
|
44,4444
|
|
8
|
579
|
14
|
|
26
|
25
|
50,9804
|
|
9
|
599
|
20
|
|
39
|
25
|
60,9375
|
|
10
|
618
|
19
|
|
58
|
22
|
72,5000
|
Заполним графу 3 и 4:
2-ой день: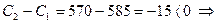 
заполняем графу 4;
3-ий день: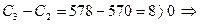 
заполняем графу 3;
4-ый день: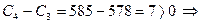 
заполняем графу 3;
5-ый день: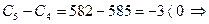 
заполняем графу 4;
6-ой день: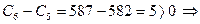 
заполняем графу 3;
7-ой день: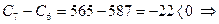 
заполняем графу 4;
8-ой день: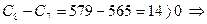 
заполняем графу 3;
9-ый день: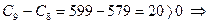 
заполняем графу 3;
10-ый день: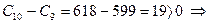 
заполняем графу 3.
Заполним графу 5:
6-ой день:
8+7+5=20;
7-ой день: 8+7+5=20;
8-ой день:
7+5+14=26;
9-ый день:
5+14+20=39;
10-ый
день:5+14+20+19=58.
Заполним графу 6:
6-ой день: 15+3=18;
7-ой день: 3+22=25;
8-ой день: 3+22=25;
9-ый день: 3+22=25;
10-ый день: 22.
Заполним графу 7:
; 
;
; 
;
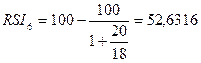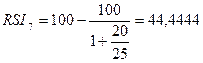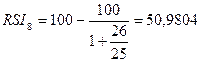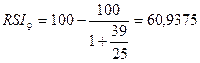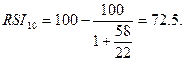
Индексы
стохастических линий %Rt, %Kt, %Dt рассчитаем по
формулам:
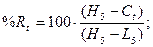
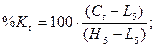
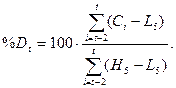
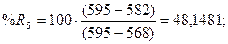
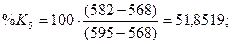
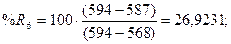
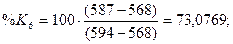
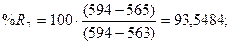
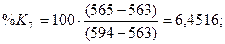
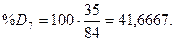
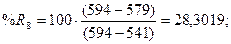
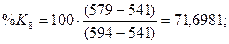
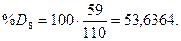
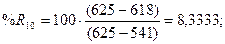
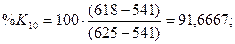
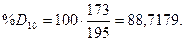
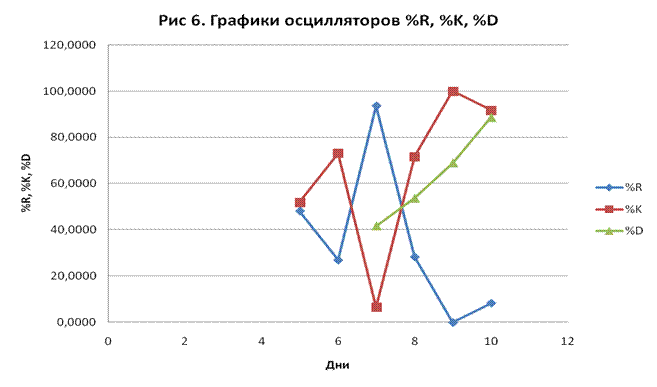
Ниже на графике (рис. 6)
приведены расчётные значения осцилляторов.
Задание 3
Выполнить различные
коммерческие расчеты, используя данные, приведенные в таблице. В условии задачи
значения параметров приведены в виде переменных. По именам переменных из
таблицы необходимо выбрать соответствующие численные значения параметров и
выполнить расчеты.
|
Сумма
|
Дата
начальная
|
Дата
конечная
|
Время в
днях
|
Время в
годах
|
Ставка
|
Число
начислений
|
|
S
|
Тн
|
Тк
|
Тдн
|
Тлет
|
i
|
M
|
|
4000000
|
10.01.02
|
20.03.02
|
90
|
5
|
45
|
4
|
3.1. Банк дал ссуду,
размером S руб. Дата выдачи ссуды – Тн, возврата – Тк.
День выдачи и день возврата считать за 1 день. Проценты рассчитываются по
простой процентной ставке i% годовых.
Найти:
3.1.1) точные проценты с
точным числом дней ссуды:
К=365 (дней) – количество
дней в году;
t= 69 (дней) – количество дней, за
которые начисляются проценты;
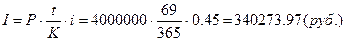
3.1.2) обыкновенные
проценты с точным числом дней ссуды:
К=360 (дней) – количество
дней в году;
t= 69 (дней) – количество дней, за
которые начисляются проценты;
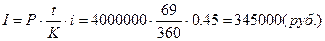
3.1.3)обыкновенные
проценты с приближенным числом дней ссуды:
К=360 (дней) – количество
дней в году;
t= 70 (дней) – количество дней, за
которые начисляются проценты;
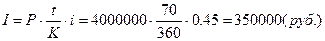
3.2. Через Тн
дней после подписания договора должник уплатит S руб. Кредит выдан под i%
годовых (проценты обыкновенные). Какова первоначальная сумма и дисконт?
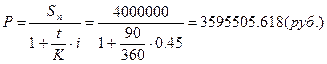
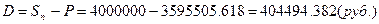
3.3. Через Тдн
дней предприятие должно получить по
векселю S руб. Банк приобрел этот вексель с дисконтом. Банк учел вексель по
учетной ставке i% годовых (год равен 360 дням). Определить полученную
предприятием сумму и дисконт.
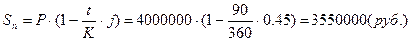
3.4. В кредитном договоре
на сумму S руб. и сроком на Тлет лет, зафиксирована ставка сложных
процентов, равная i% годовых. Определите наращенную сумму.
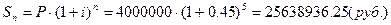
3.5. Ссуда, размером S
руб. предоставлена на Тлет. Проценты сложные, ставка – i% годовых.
Проценты начисляются m раз в году. Вычислить наращенную сумму.
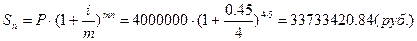
3.6. Вычислить
эффективную ставку процента, если банк начисляет проценты m раз в году, исходя
из номинальной ставки i% годовых.
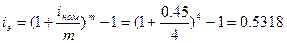или 53,18%
3.7. Определить какой
должна быть номинальная ставка при начислении процентов m раз в году, чтобы
обеспечить эффективную ставку i% годовых.
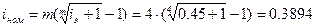или 38,94%
3.8. Через Тлет
предприятию будет выплачена сумма S руб. Определить ее современную стоимость
при условии, что применяется сложная процентная ставка i% годовых.
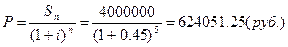
3.9. Через Тлет
по векселю должна быть выплачена сумма S руб. Банк учел вексель по сложной
учетной ставке i% годовых. Определить дисконт.
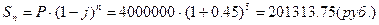
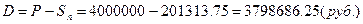
3.10. В течение Тлет
лет на расчетный счет в конце каждого года поступает по S руб., на которые m
раз в году начисляются проценты по сложной годовой ставке i%. Определить сумму
на расчетном счете к концу указанного срока.
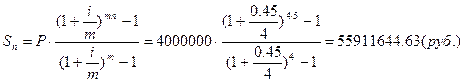
Список использованной литературы:
1. Финансовая математика: математическое моделирование финансовых операций: Учеб.
пособие / Под ред. В.А. Половникова и А.И. Пилипенко. - М.: Вузовский учебник,
2004.
2.
Финансовая математика:
Методические указания по изучению дисциплины и контрольные задания. Для
студентов 4-го курса специальности 060400 «Финансы и кредит» / ВЗФЭИ. - М.:
Финстатинформ, 2002.