ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КОНТРОЛЬНАЯ РАБОТА
по предмету
"Эконометрика"
Выполнил:
специальность:
Бухгалтерский
учет, анализ и аудит
группа №
№
МОСКВА
2004
ВАРИАНТ № 28
I
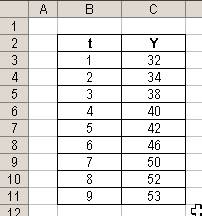
Таблица 1. Исходные данные.
|
t
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
Y
|
32
|
34
|
38
|
40
|
42
|
46
|
50
|
52
|
53
|
На
основании данных, приведенных в табл. 1. Требуется:
1) построить линейную модель Y(t) = ao + a1t, параметры которой оценить МНК;
2) оценить адекватность построенной
модели на основе исследования:
-
случайности
остаточной компоненты по критерию пиков;
-
независимости
уровней ряда остатков по d-критерию
(в качестве критических значений следует
использовать уровни d1 =
1,08 и d2 = 1,36) и по
первому коэффициенту автокорреляции,
критический уровень которого r(1) =
0,36;
-
нормальности
распределения остаточной компоненты по R/S-критерию
с критическими уровнями 2,7 – 3,7;
3) для оценки точности модели
используйте среднеквадратическое отклонение и среднюю по модулю относительную
ошибку;
4) построить точечный и интервальный прогнозы на два шага
вперед (для вероятности
Р= 70% используйте коэффициент = 1,12);
5) отобразить на графике фактические
данные, результаты расчетов и прогнозирования.
РЕШЕНИЕ
Ввод исходных данных
1.
оценка параметров
модели.
1.1. Оценка параметров модели с помощью надстройки EXCEL Анализ данных.
Построим линейную
однопараметрическую модель регрессии Y от
t. Для проведения
регрессионного анализа выполните следующие действия:
·
Выберите команду Сервис Þ
Анализ данных.
·
В диалоговом окне Анализ данных выберите инструмент Регрессия (рис.
2.8), а затем щелкните на кнопке ОК.
·
В диалоговом окне Регрессия в
поле Входной интервал Y введите адрес одного
диапазона ячеек, который представляет
зависимую переменную. В поле Входной интервал Х введите адрес диапазона,
который содержат значения независимой переменной t (рис. 2.9).
·
Если выделены и заголовки столбцов, то установить флажок Метки в первой строке.
·
Выберите параметры вывода. В данном примере Новая рабочая книга.
·
В поле График подбора поставьте флажок.
·
В поле Остатки поставьте необходимые флажки и нажмите
кнопку ОК.
Рис. 2.8. Выбран инструмент анализа Регрессия
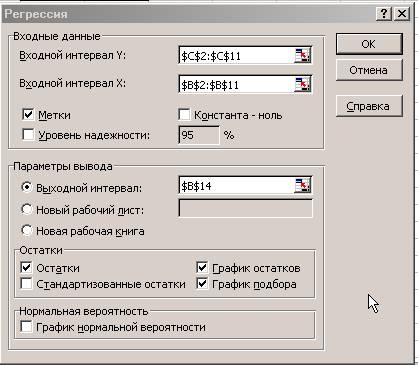
Рис. 2.9. Ввод исходных данных для Регрессии
Результат регрессионного анализа содержится
в нижеприведенных таблицах.
|
ВЫВОД ИТОГОВ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Регрессионная
статистика
|
|
|
|
|
|
|
Множественный R
|
0,9941
|
|
|
|
|
|
|
R-квадрат
|
0,988235
|
|
|
|
|
|
|
Нормированный R-квадрат
|
0,986555
|
|
|
|
|
|
|
Стандартная ошибка
|
0,894427
|
|
|
|
|
|
|
Наблюдения
|
9
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный анализ
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость
F
|
|
|
Регрессия
|
1
|
470,4
|
470,4
|
588
|
5,16E-08
|
|
|
Остаток
|
7
|
5,6
|
0,8
|
|
|
|
|
Итого
|
8
|
476
|
|
|
|
|
|
Таблица 2.5
|
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
Нижние
95%
|
Верхние
95%
|
|
Y-пересечение
|
a0
|
29
|
0,649786
|
44,63006
|
7,41E-10
|
27,4635
|
30,5365
|
|
t
|
a1
|
2,8
|
0,11547
|
24,24871
|
5,16E-08
|
2,526957
|
3,073043
|
|
|
|
|
|
|
|
|
|
ВЫВОД ОСТАТКА
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Наблюдение
|
Предсказанное
Y
|
Остатки
|
|
|
|
|
|
1
|
31,8
|
0,2
|
|
|
|
|
|
2
|
34,6
|
-0,6
|
|
|
|
|
|
3
|
37,4
|
0,6
|
|
|
|
|
|
4
|
40,2
|
-0,2
|
|
|
|
|
|
5
|
43
|
-1
|
|
|
|
|
|
6
|
45,8
|
0,2
|
|
|
|
|
|
7
|
48,6
|
1,4
|
|
|
|
|
|
8
|
51,4
|
0,6
|
|
|
|
|
|
9
|
54,2
|
-1,2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Во втором столбце табл. 2.5
содержатся коэффициенты уравнения регрессии a0, a1, в третьем столбце – стандартные ошибки коэффициентов уравнения
регрессии, а в четвертом – t-статистика,
используемая для проверки
значимости коэффициентов уравнения регрессии.
Уравнение регрессии зависимости Yt,
от tt (время) имеет вид:
Y(t) =29+2,8t
При вычислении
«вручную» по формуле получаем те же результаты:
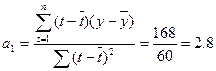
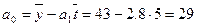
Таблица 2.7
|
|
t
|
Y
|
t-tcp
|
(t-tcp)2
|
y-ycp
|
(t-tcp)( y-ycp)
|
|
|
1
|
32
|
-4
|
16
|
-11,00
|
44,00
|
|
|
2
|
34
|
-3
|
9
|
-9,00
|
27,00
|
|
|
3
|
38
|
-2
|
4
|
-5,00
|
10,00
|
|
|
4
|
40
|
-1
|
1
|
-3,00
|
3,00
|
|
|
5
|
42
|
0
|
0
|
-1,00
|
0,00
|
|
|
6
|
46
|
1
|
1
|
3,00
|
3,00
|
|
|
7
|
50
|
2
|
4
|
7,00
|
14,00
|
|
|
8
|
52
|
3
|
9
|
9,00
|
27,00
|
|
|
9
|
53
|
4
|
16
|
10,00
|
40,00
|
|
Сумма
|
45
|
387
|
0,00
|
60,00
|
344,00
|
168,00
|
|
Среднее
|
5
|
43
|
|
|
|
|
2.
оценка качества построенной модели. Для этого исследуем адекватность модели. Модель
является адекватной, если математическое ожидание значений остаточного ряда
близко или равно нулю, и если значения остаточного ряда случайны, независимы и
подчинены нормальному закону распределения.
·
При проверке независимости (отсутствие
автокорреляции) определяется отсутствие в ряду остатков систематической
составляющей, например, с помощью d-критерия
Дарбина–Уотсона по формуле):
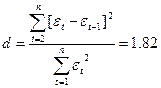
Так
как попало в интервал от d2 до 2 (рис. 2.10), значит модель уровня
ряда остатков независима, автокорреляции нет, свойство независимости
выполняется. Модель по этому критерию адекватна.
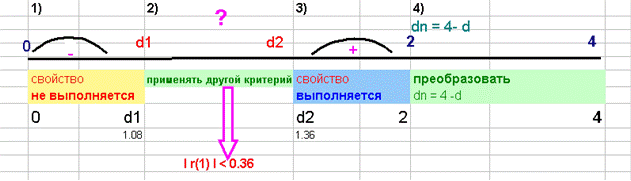 Рис. 2.10.
Рис. 2.10.
·
Проверку случайности уровней ряда остатков
проведем на основе критерия поворотных точек
(формула (2.6)).
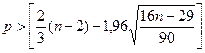
Формула 2.6
·
Количество
поворотных точек равно 4 (рис. 2.11). Неравенство выполняется (4>2).
Следовательно, свойство случайности выполняется. Модель по этому критерию адекватна.
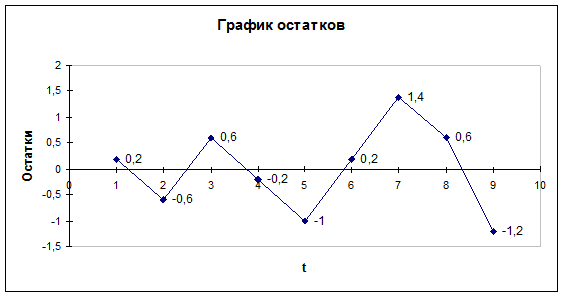
Рис. 2.11. График
остатков
·
Соответствие ряда остатков нормальному
закону распределения определим при
помощи RS-критерия:
|
Наблюдение
|
Предсказанное
Y
|
Остатки
E(t)
|
E(t)-E(t-1)
|
(E(t)-(E(t-1))^2
|
E(t)^2
|
|
1
|
31,8
|
0,2
|
|
|
0,04
|
|
2
|
34,6
|
-0,6
|
-0,8
|
0,64
|
0,36
|
|
3
|
37,4
|
0,6
|
1,2
|
1,44
|
0,36
|
|
4
|
40,2
|
-0,2
|
-0,8
|
0,64
|
0,04
|
|
5
|
43
|
-1
|
-0,8
|
0,64
|
1
|
|
6
|
45,8
|
0,2
|
1,2
|
1,44
|
0,04
|
|
7
|
48,6
|
1,4
|
1,2
|
1,44
|
1,96
|
|
8
|
51,4
|
0,6
|
-0,8
|
0,64
|
0,36
|
|
9
|
54,2
|
-1,2
|
-1,8
|
3,24
|
1,44
|
|
СУММА
|
|
|
|
10,12
|
5,56
|
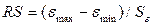
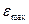 – максимальный уровень ряда остатков,
– максимальный уровень ряда остатков, 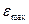 = 1,4;
= 1,4;
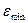 – минимальный уровень ряда остатков,
– минимальный уровень ряда остатков,
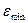 = – 1,2;
= – 1,2;
 – среднеквадратичное отклонение,
– среднеквадратичное отклонение,
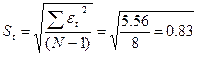
RS=[1,4–(-1,2)] / 0,83= 3,11.
Расчетное значение попадает в интервал (2,7–3,7),
следовательно, выполняется свойство нормальности распределения. Модель по этому
критерию адекватна.
·
Проверка равенства нулю математического ожидания
уровней ряда остатков.
В нашем случае 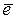 = 0, поэтому гипотеза о равенстве математического ожидания
значений остаточного ряда нулю выполняется.
= 0, поэтому гипотеза о равенстве математического ожидания
значений остаточного ряда нулю выполняется.
В табл. 2.8 собраны данные анализа ряда остатков.
Таблица 2.8. Анализ ряда остатков
|
Проверяемое
свойство
|
Используемые статистики
|
Граница
|
Вывод
|
|
наименование
|
значение
|
нижняя
|
верхняя
|
|
Независимость
|
d-критерий
Дарбина–Уотсона
|
d=1,82
|
1,36
|
2
|
адекватна
|
|
Случайность
|
Критерий пиков (поворотных
точек)
|
4 > 2
|
2
|
адекватна
|
|
Нормальность
|
RS-критерий
|
3,11
|
2,6
|
3,7
|
адекватна
|
|
Среднее = 0
|
t-статистика Стьюдента
|
0,000
|
-2,179
|
2,179
|
адекватна
|
|
Вывод: Модель статистически адекватна
|
|
|
|
|
|
|
|
3.
Построить точечный и интервальный прогнозы на
два шага вперед (для
вероятности 70% использовать t = 1,12):
Y10= a0
+ a1t =29 + 2,8t = 29 + 2,8 x 10 = 57;
Y11= a0 + a1t =29 + 2,8t = 29 + 2,8 x 11 =
59.8;
Для построения интервального прогноза рассчитаем
доверительный интервал. Примем значение уровня значимости α = 0,3, следовательно,
доверительная вероятность равна 70%, а критерий Стьюдента при 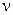 = n –2 =7 равен
1,12. Ширину доверительного интервала вычислим по формуле (3.10):
= n –2 =7 равен
1,12. Ширину доверительного интервала вычислим по формуле (3.10):
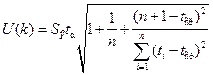 ,
,
где
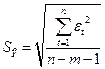 =0,8944,
=0,8944, 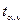 = 1,12,
= 1,12,  ,
, 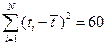 (находим из табл. 2.7),
(находим из табл. 2.7),
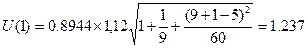
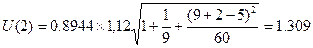
Далее
вычисляем верхнюю и нижнюю границы прогноза (табл. 2.9):
Таблица 2.9.
|
|
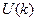
|
Прогноз
|
Формула
|
Верхняя граница
|
Нижняя граница
|
|
10
|
U(1)=1,237
|
57
|
Прогноз + U1
|
58,237
|
55,763
|
|
11
|
U(2)=1,309
|
59,8
|
Прогноз – U1
|
61,109
|
58,491
|
4.
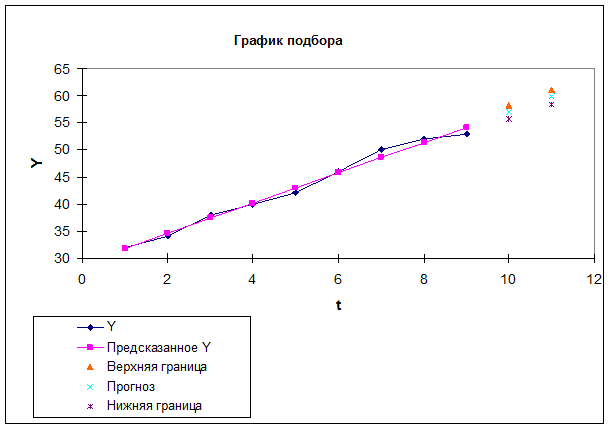
Отобразить на графике фактические данные,
результаты расчетов и прогнозирования.
II
1 – построить матрицу коэффициентов парной корреляции Y(t) с
X1(t) и X2(t) и выбрать
фактор, наиболее тесно связанный с зависимой переменной Y(t);
2 – построить линейную
однопараметрическую модель регрессии Y(t) = ao + a1 X(t);
3 – оценить качество построенной модели, исследовав ее адекватность
и точность;
4 – для модели регрессии рассчитать коэффициент эластичности и бета-коэффициент;
5 -
построить точечный и интервальный
прогнозы на два шага вперед по модели регрессии (для вероятности Р = 70%
используйте коэффициент 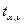 = 1,12) (прогнозные оценки фактора X(t) на два шага вперед получить на основе
среднего прироста от фактически достигнутого уровня).
= 1,12) (прогнозные оценки фактора X(t) на два шага вперед получить на основе
среднего прироста от фактически достигнутого уровня).
Таблица 2. Исходные данные.
|
|
ФАКТОРЫ
|
|
Y
|
X1
|
X2
|
|
32
|
90
|
55
|
|
34
|
87
|
57
|
|
38
|
85
|
54
|
|
40
|
86
|
59
|
|
42
|
82
|
57
|
|
46
|
80
|
60
|
|
50
|
81
|
63
|
|
52
|
78
|
66
|
|
53
|
76
|
64
|
РЕШЕНИЕ
5.
Ввод исходных данных. Результат показан на рис. 3.7.
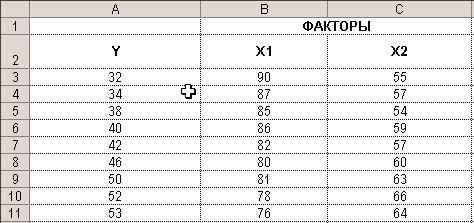
Рис. 3.7. Исходные данные введены в Excel
1.
ПОСТРОЕНИЕ СИСТЕМЫ ПОКАЗАТЕЛЕЙ (ФАКТОРОВ). АНАЛИЗ МАТРИЦЫ КОЭФФИЦИЕНТОВ
ПАРНОЙ КОРРЕЛЯЦИИ. ВЫБОР НАИБОЛЕЕ СУЩЕСТВЕННОГО ФАКТОРА Х
T..
Для
того чтобы выбрать фактор наиболее тесно связанный с зависимой переменной,
оценим величину влияния факторов при помощи коэффициента корреляции.
Для проведения
корреляционного анализа с помощью EXCEL выполните следующие действия:
1) Данные
для корреляционного анализа должны располагаться в смежных диапазонах
ячеек.
2) Выберите
команду СервисÞАнализ
данных.
3) В
диалоговом окне Анализ данных выберите инструмент Корреляция (рисунок 2.), а затем
щелкните на кнопке ОК.
4) В
диалоговом окне Корреляция в поле
Входной интервал необходимо ввести
диапазон ячеек, содержащих исходные данные. Если выделены и заголовки столбцов,
то установить флажок Метки в первой строке (рисунок 3.).
5) Выберите
параметры вывода.
6) ОК.
|
Результат корреляционного анализа
|
|
|
|
|
|
|
|
|
|
Y
|
X1
|
X2
|
|
Y
|
1
|
|
|
|
X1
|
-0,958245799
|
1
|
|
|
X2
|
0,90837152
|
-0,82044571
|
1
|
Анализ матрицы коэффициентов парной
корреляции показывает, что зависимая переменная Yt имеет более тесную связь с x1t.
вычисление коэффициентов
корреляции без ПЭВМ.
Коэффициент корреляции определяется по формуле
(используем данные таблицы 5.2):
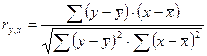 =ryx1 = -269/
=ryx1 = -269/ 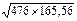 = -269/280.725=-0,958245799
= -269/280.725=-0,958245799
Аналогично вычисляются
остальные коэффициенты корреляции.
Таблица 5.2
|
Y
|
X1
|
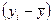
|
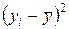
|
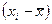
|
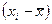 2 2
|
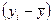 * *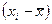
|
|
32
|
90
|
-11
|
121
|
7,22
|
52,16
|
-79,44
|
|
34
|
87
|
-9
|
81
|
4,22
|
17,83
|
-38,00
|
|
38
|
85
|
-5
|
25
|
2,22
|
4,94
|
-11,11
|
|
40
|
86
|
-3
|
9
|
3,22
|
10,38
|
-9,67
|
|
42
|
82
|
-1
|
1
|
-0,78
|
0,60
|
0,78
|
|
46
|
80
|
3
|
9
|
-2,78
|
7,72
|
-8,33
|
|
50
|
81
|
7
|
49
|
-1,78
|
3,16
|
-12,44
|
|
52
|
78
|
9
|
81
|
-4,78
|
22,83
|
-43,00
|
|
53
|
76
|
10
|
100
|
-6,78
|
45,94
|
-67,78
|
|
|
|
0,00
|
476,00
|
0,00
|
165,56
|
-269,00
|
Yср = 43
X1ср= 82,78
6.
оценка параметров модели.
6.1. Оценка
параметров модели с помощью надстройки EXCEL Анализ данных.
Построим линейную однопараметрическую модель регрессии
Y от X. Для проведения регрессионного анализа выполните
следующие действия:
·
Выберите команду Сервис Þ Анализ данных.
·
В диалоговом окне
Анализ данных
выберите инструмент Регрессия (рис. 3.8), а затем щелкните на кнопке ОК.
·
В диалоговом окне
Регрессия в поле Входной интервал Y введите
адрес одного диапазона ячеек, который
представляет зависимую переменную. В поле Входной интервал Х введите адрес диапазона, который содержат значения
независимой переменной t (рис. 3.9).
·
Если выделены и
заголовки столбцов, то установить флажок Метки в первой строке.
·
Выберите
параметры вывода. В данном примере Новая рабочая книга.
·
В поле График подбора поставьте
флажок.
·
В поле Остатки поставьте необходимые флажки и нажмите кнопку ОК.
Рис. 3.8.
Выбран инструмент анализа Регрессия
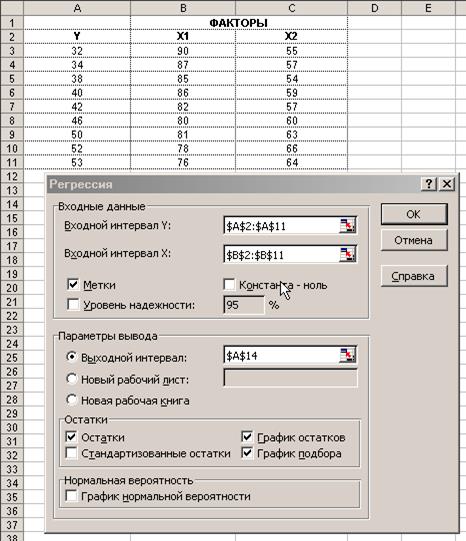
Рис. 3.9. Ввод исходных данных для Регрессии
Результат
регрессионного анализа содержится в нижеприведенных таблицах.
|
ВЫВОД ИТОГОВ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Регрессионная
статистика
|
|
|
|
|
|
|
|
|
Множественный R
|
0,958245799
|
|
|
|
|
|
|
|
|
R-квадрат
|
0,918235012
|
|
|
|
|
|
|
|
|
Нормированный R-квадрат
|
0,9065543
|
|
|
|
|
|
|
|
|
Стандартная
ошибка
|
2,357969291
|
|
|
|
|
|
|
|
|
Наблюдения
|
9
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный анализ
|
|
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость
F
|
|
|
|
|
Регрессия
|
1
|
437,0798658
|
437,0799
|
78,61122
|
4,7E-05
|
|
|
|
|
Остаток
|
7
|
38,92013423
|
5,560019
|
|
|
|
|
|
|
Итого
|
8
|
476
|
|
|
|
|
|
|
|
Таблица 3.5.
|
|
|
|
|
|
|
|
|
Переменная
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
Нижние
95%
|
Верхние
95%
|
Нижние
95,0%
|
Верхние
95,0%
|
|
Y-пересечение
|
a0
|
177,5
|
15,19015457
|
11,6852
|
7,6E-06
|
141,581
|
213,419
|
141,581
|
213,419
|
|
X1
|
a1
|
-1,624832215
|
0,183259402
|
-8,8663
|
4,7E-05
|
-2,05817
|
-1,19149
|
-2,05817
|
-1,19149
|
|
|
|
|
|
|
|
|
|
|
|
Таблица
3.6. ВЫВОД ОСТАТКА
|
|
|
|
|
|
|
|
|
Наблюдение
|
Предсказанное
Y
|
Остатки
|
|
|
|
|
|
|
|
1
|
31,26510067
|
0,734899329
|
|
|
|
|
|
|
|
2
|
36,13959732
|
-2,139597315
|
|
|
|
|
|
|
|
3
|
39,38926174
|
-1,389261745
|
|
|
|
|
|
|
|
4
|
37,76442953
|
2,23557047
|
|
|
|
|
|
|
|
5
|
44,26375839
|
-2,263758389
|
|
|
|
|
|
|
|
6
|
47,51342282
|
-1,513422819
|
|
|
|
|
|
|
|
7
|
45,8885906
|
4,111409396
|
|
|
|
|
|
|
|
8
|
50,76308725
|
1,236912752
|
|
|
|
|
|
|
|
9
|
54,01275168
|
-1,012751678
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Во втором столбце табл. 3.5
содержатся коэффициенты уравнения регрессии a0, a1, в третьем столбце – стандартные ошибки коэффициентов уравнения
регрессии, а в четвертом – t-статистика,
используемая для проверки
значимости коэффициентов уравнения регрессии.
Уравнение регрессии зависимости Yt,
(прибыль коммерческого банка) от tt
(время) имеет вид:
Y(X) = 177,5 -1,62X
При вычислении
«вручную» по формуле (3.4) получаем те же результаты:
7.
оценка качества построенной модели. Для этого исследуем адекватность модели. Модель
является адекватной, если математическое ожидание значений остаточного ряда
близко или равно нулю, и если значения остаточного ряда случайны, независимы и
подчинены нормальному закону распределения.
8.
·
При проверке независимости (отсутствие
автокорреляции) определяется отсутствие в ряду остатков систематической
составляющей, например, с помощью d-критерия
Дарбина–Уотсона по формуле (3.7):
|
Наблюдение
|
Предсказанное
Y
|
Остатки
E(t)
|
E(t)-E(t-1)
|
(E(t)-(E(t-1))^2
|
E(t)^2
|
|
1
|
31,265
|
0,735
|
|
|
0,540
|
|
2
|
36,140
|
-2,140
|
-2,874
|
8,263
|
4,578
|
|
3
|
39,389
|
-1,389
|
0,750
|
0,563
|
1,930
|
|
4
|
37,764
|
2,236
|
3,625
|
13,139
|
4,998
|
|
5
|
44,264
|
-2,264
|
-4,499
|
20,244
|
5,125
|
|
6
|
47,513
|
-1,513
|
0,750
|
0,563
|
2,290
|
|
7
|
45,889
|
4,111
|
5,625
|
31,639
|
16,904
|
|
8
|
50,763
|
1,237
|
-2,874
|
8,263
|
1,530
|
|
9
|
54,013
|
-1,013
|
-2,250
|
5,061
|
1,026
|
|
СУММА
|
|
|
|
87,735
|
38,380
|
d'= 4 -2,2859=1,714
Так
как d' попало в интервал от d2 до 2 (рис.
3.10), значит модель уровня ряда
остатков независима, автокорреляции нет, свойство независимости выполняется.
Модель по этому критерию адекватна.
 Рис. 3.10.
Рис. 3.10.
·
Проверку случайности уровней ряда остатков
проведем на основе критерия поворотных точек.
В случайном
ряду чисел должно выполняться строгое неравенство: р > [2(N-2)/3-2Ö(16N-29)/90]. Количество поворотных точек равно 4 (рис. 3.11).
Неравенство выполняется (4>2). Следовательно, свойство случайности выполняется.
Модель по этому критерию адекватна.
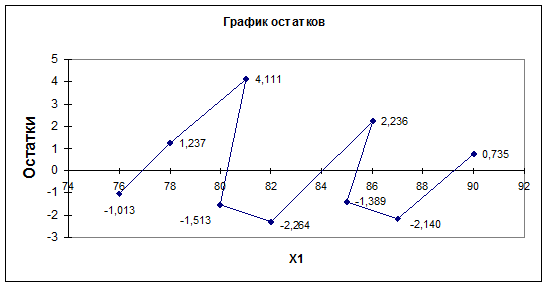
Рис. 3.11. График
остатков
·
Соответствие ряда остатков нормальному
закону распределения определим при
помощи RS-критерия:
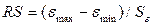
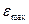 – максимальный уровень ряда остатков,
– максимальный уровень ряда остатков, 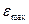 = 4,1114;
= 4,1114;
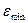 – минимальный уровень ряда остатков,
– минимальный уровень ряда остатков,
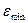 = – 2,2637;
= – 2,2637;
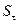 – среднеквадратичное отклонение,
– среднеквадратичное отклонение,
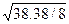
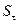 =
=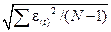 = =2,19;
= =2,19;
RS=[4,1114–(-2,2637)] / 2,19= 2,91.
Расчетное значение попадает в интервал (2,7–3,7),
следовательно, выполняется свойство нормальности распределения. Модель по этому
критерию адекватна.
·
Проверка равенства нулю математического ожидания
уровней ряда остатков осуществляется
с использованием t-критерия Стьюдента
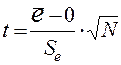 ,
,
где 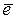 – среднее значение
уровней остаточного ряда , Sе -
среднее квадратичное отклонение уровней остаточного ряда
– среднее значение
уровней остаточного ряда , Sе -
среднее квадратичное отклонение уровней остаточного ряда
В нашем случае 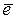 = 0, поэтому гипотеза о равенстве математического ожидания
значений остаточного ряда нулю выполняется.
= 0, поэтому гипотеза о равенстве математического ожидания
значений остаточного ряда нулю выполняется.
Для расширенной
характеристики модели регрессии вычислим несколько дополнительных показателей:
коэффициент детерминации R2
и коэффициент множественной корреляции R. Эти характеристики приведены в
таблице 3.7 протокола ЕХСЕL.
Таблица 3.7
|
Множественный R
|
0,958245799
|
|
R-квадрат
|
0,918235012
|
|
Нормированный R-квадрат
|
0,9065543
|
|
Стандартная ошибка
|
2,357969291
|
|
Наблюдения
|
9
|
Коэффициент детерминации:
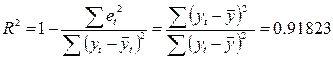
R2 показывает долю вариации результативного
признака под воздействием изучаемых факторов. Следовательно, более 91.8 % вариации
зависимой переменной учтено в модели и обусловлено влиянием включенного
фактора.
R - коэффициент множественной
корреляции. R = 0.9582 показывает
тесноту связи зависимой Y c факторами Х,
включенными в модель. в случае
однофакторной модели R совпадает с ryx1.
В табл. 3.8 собраны данные анализа ряда остатков.
Таблица 3.8. Анализ ряда остатков
|
Проверяемое
свойство
|
Используемые статистики
|
Граница
|
Вывод
|
|
наименование
|
значение
|
нижняя
|
верхняя
|
|
Независимость
|
d-критерий
Дарбина–Уотсона
|
d=2,2859
dn
=4 -2,285=1,714
|
1,36
|
2
|
адекватна
|
|
Случайность
|
Критерий пиков (поворотных
точек)
|
4 > 2
|
2
|
адекватна
|
|
Нормальность
|
RS-критерий
|
2,91
|
2,6
|
3,7
|
адекватна
|
|
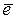 = 0 = 0
|
t-статистика Стьюдента
|
0,000
|
-2,179
|
2,179
|
адекватна
|
|
Вывод: Модель статистически
адекватна
|
|
|
|
|
|
|
|
9.
ОПРЕДЕЛИМ
КОЭФФИЦИЕНТ ЭЛАСТИЧНОСТИ И β-КОЭФФИЦИЕНТ
8.1 Коэффициент эластичности показывает, на сколько
процентов изменится Y если X1 изменится на
1%.
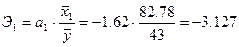 %
%
Таким образом, при изменении X1 на 1% Y изменится на -3.127%
8.2 β-коэффициент показывает, на какую долю в
среднем изменится среднеквадратическое отклонение зависимой переменной Y при
изменении X1 на одно свое
среднеквадратическое отклонение при фиксированных значениях остальных объясняющих
переменных.
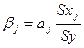
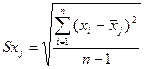
β1= - 0.958
10.
ОПРЕДЕЛИМ
ТОЧЕЧНЫЕ И ИНТЕРВАЛЬНЫЕ ПРОГНОЗНЫЕ ОЦЕНКИ ПРИБЫЛИ КОММЕРЧЕСКОГО БАНКА НА ДВА
КВАРТАЛА ВПЕРЕД (T0,7 = 1,12 для n-2= 9-2 =7).
Для
вычисления прогнозных оценок Y на основе построенной модели необходимо получить
прогнозные оценки фактора Х.
Получим
прогнозные оценки фактора на основе величины его среднего абсолютного прироста
САП.
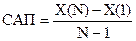 ;
;
CАП = (76-90)/(9-1) = -1.75
Xp(N+l) = X(N) + l ∙ САП;
l=1
Xp(10) = Х(9) -1.75 ∙ 1 = 76 -1,75 ∙ 1 =74.25
l=2
Xp(11) = Х(9) -1,75 ∙ 2 = 76 -1,75 ∙ 2 =72.5;
Для получения прогнозных оценок
зависимой переменной подставим в модель
Yt =
177,5-1,62*X1 найденные
прогнозные значения фактора Х:
Y10 =
=177,5-1,62* X10=177,5-1,62*74.25=57.215
Y11 =
=177,5-1,62* X11=177,5-1,62*72.5=60.05
Определим доверительный интервал
прогноза, который будет иметь следующие границы:
-
Верхняя граница
прогноза: Yp(N+l) + U(l);
-
Нижняя граница
прогноза: Yp(N+l) - U(l).
Величина
U(l) имеет вид:
и(l) = S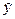 ta
ta , где
, где
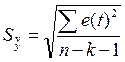 - стандартная ошибка - эта
характеристика приведена в таблице
протокола ЕХСЕL и равна 2,357969291;
- стандартная ошибка - эта
характеристика приведена в таблице
протокола ЕХСЕL и равна 2,357969291;
ta -является табличным значением критерия
Стьюдента для уровня значимости a и для числа степеней свободы, равного N-2. В нашем примере t0,7 =
1,12;
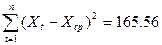
|
Y
|
X1
|
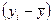
|
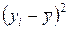
|
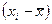
|
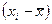 2 2
|
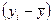 * *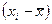
|
|
32
|
90
|
-11
|
121
|
7,22
|
52,16
|
-79,44
|
|
34
|
87
|
-9
|
81
|
4,22
|
17,83
|
-38,00
|
|
38
|
85
|
-5
|
25
|
2,22
|
4,94
|
-11,11
|
|
40
|
86
|
-3
|
9
|
3,22
|
10,38
|
-9,67
|
|
42
|
82
|
-1
|
1
|
-0,78
|
0,60
|
0,78
|
|
46
|
80
|
3
|
9
|
-2,78
|
7,72
|
-8,33
|
|
50
|
81
|
7
|
49
|
-1,78
|
3,16
|
-12,44
|
|
52
|
78
|
9
|
81
|
-4,78
|
22,83
|
-43,00
|
|
53
|
76
|
10
|
100
|
-6,78
|
45,94
|
-67,78
|
|
|
745
|
0,00
|
476,00
|
0,00
|
165,56
|
-269,00
|
Хср=745/9=82.78
Для прогноза на два шага
имеем:
U(1) = 2,357969291∙ 1,12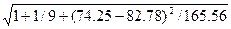 = 3.2589
= 3.2589
U(2) = 2,357969291∙ 1,12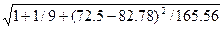 = 3.4615
= 3.4615
Результаты
прогнозных оценок по модели регрессии представим в таблице:
|
Время t
|
Шаг k
|
Прогноз Yp(t)
|
Нижняя граница
|
Верхняя граница
|
|
10
|
1
|
57,215
|
53,929
|
60,501
|
|
11
|
2
|
60,05
|
56,56
|
63,540
|
11.
Отобразить на графике
фактические данные, результаты расчетов и прогнозирования.
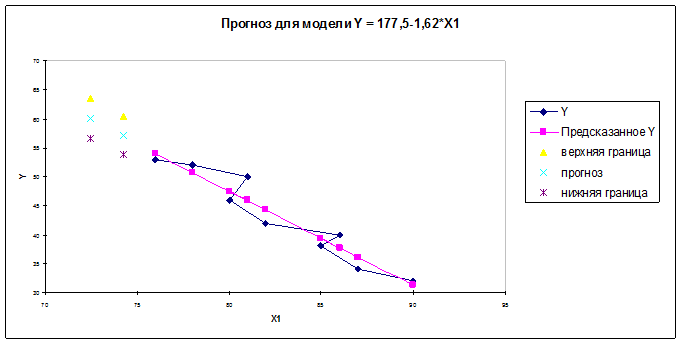
Рис. 3.16. Результаты моделирования и
прогнозирования