Федеральное агентство по образованию
Всероссийский заочный финансово –
экономический институт
Кафедра математики и информатики
КОНТРОЛЬАЯ РАБОТА
по дисциплине «Финансовая математика»
на тему
Вариант №7
Исполнитель: Наймушина Оксана Владимировна
Факультет:
Финансово-кредитный
Специальность: Финансы и
кредит
Группа: 4ФКп-2
№ 03ФФД10857
Руководитель: Поддубная Марина Львовна
Барнаул
2006
Задание 1.
В каждом варианте приведены поквартальные данные о
кредитах от коммерческого банка на жилищное строительство (в условных единицах)
за 4 года (всего 16 кварталов, первая строка соответствует первому кварталу
первого года).
Требуется:
1) Построить адаптивную мультипликативную модель
Хольта-Уинтерса с учетом сезонного фактора, приняв параметры сглаживания α1=0,3;
α2=0,6; α3=0,3.
2) Оценить точность построенной модели с
использованием средней относительной ошибки аппроксимации.
3) Оценить адекватность построенной Модели на основе
исследования:
3.1
случайности
остаточной компоненты по критерию пиков;
3.2
независимости
уровней ряда остатков по d-критерию
(критические значения d1=1,10 и d2=1.37) и по первому коэффициенту автокорреляции при
критическом значении г1= 0,32;
3.3
нормальности
распределения остаточной компоненты по R/S-критерию с
критическими значениями от 3до 4,21.
4) Построить точечный прогноз на 4 шага вперед, т.е.
на 1 год.
5) Отразить на графике фактические, расчетные и
прогнозные данные.
|
Квартал
|
Вариант
|
|
7
|
|
1
|
38
|
|
2
|
48
|
|
3
|
57
|
|
4
|
37
|
|
5
|
40
|
|
6
|
52
|
|
7
|
63
|
|
8
|
38
|
|
9
|
44
|
|
10
|
56
|
|
11
|
67
|
|
12
|
41
|
|
13
|
49
|
|
14
|
60
|
|
18
|
72
|
|
16
|
44
|
Задание 2.
Даны цены (открытия, максимальная, минимальная и
закрытия) за 10 дней. Интервал сглаживания принять равным пяти дням.
Рассчитать:
2.1
экспоненциальную скользящую среднюю;
2.2
момент;
2.3
скорость изменения цен;
2.4
индекс относительной силы;
2.5
%К, %К и %D.
Расчеты проводить для всех дней, для которых эти
расчеты можно выполнить на основании имеющихся данных.
|
Вариант 7
|
|
Дни
|
Цены
|
|
макс.
|
мин.
|
закр.
|
|
1
|
663
|
605
|
610
|
|
2
|
614
|
577
|
614
|
|
3
|
639
|
580
|
625
|
|
4
|
625
|
572
|
574
|
|
5
|
600
|
553
|
563
|
|
6
|
595
|
563
|
590
|
|
7
|
608
|
590
|
598
|
|
8
|
610
|
573
|
580
|
|
9
|
595
|
575
|
595
|
|
10
|
600
|
580
|
580
|
Задание 3.
Выполнить различные коммерческие расчеты, используя
данные, приведенные в таблице. В условии задачи значения параметров приведены в
виде переменных. Например, S означает некую
сумму средств в рублях, Тлет - время в годах, i - ставку в процентах и т.д.
По именам переменных из таблицы необходимо выбрать
соответствующие численные значения параметров и выполнить расчеты.
|
Вариант
|
Сумма
|
Дата начальная
|
Дата конечная
|
Время в днях
|
Время в годах
|
Ставка
|
Число начислений
|
|
S
|
Тн
|
Тк
|
Тдн
|
Тлет
|
i
|
m
|
|
7
|
3500000
|
11.01.2002
|
19.03.2002
|
90
|
5
|
40
|
4
|
3.1. Банк выдал ссуду, размером S руб. Дата выдачи ссуды - Тн, возврата - Тк.
День выдачи и день возврата считать за 1 день. Проценты рассчитываются по
простой процентной ставке 1% годовых.
Найти:
3.1 1) точные проценты с точным числом дней ссуды;
3.1.2) обыкновенные проценты с точным числом дней
ссуды;
3.1.3) обыкновенные проценты с приближенным числом
дней ссуды.
3.2. Через Тдн дней после подписания
договора должник уплатит S руб. Кредит
выдан под i% годовых (проценты
обыкновенные). Какова первоначальная сумма и дисконт?
3.3. Через Тдн дней предприятие должно
получить по векселю S руб. Банк приобрел этот вексель
с дисконтом. Банк учел вексель по учетной ставке i% годовых (год равен 360 дням). Определить полученную
предприятием сумму и дисконт.
3.4. В кредитном договоре на сумму S руб. и сроком на Тдн лет, зафиксирована
ставка сложных процентов, равная i% годовых.
Определить наращенную сумму.
3.5. Ссуда, размером S руб. предоставлена на Тлет. Проценты
сложные, ставка - i% годовых. Проценты начисляются m раз в году.
Вычислить наращенную сумму.
3.6. Вычислить эффективную ставку процента, если банк
начисляет проценты от раз в году, исходя из номинальной ставки i% годовых.
3.7. Определить, какой должна быть номинальная ставка
при начислении процентов m раз в году,
чтобы обеспечить эффективную ставку i%
годовых.
3.8. Через Тлет предприятию будет выплачена
сумма S руб. Определить ее современную стоимость при условии,
что применяется сложная процентная ставка i% годовых.
3.9. Через Тлет по векселю должна быть
выплачена сумма S руб. Банк учел вексель по
сложной учетной ставке i% годовых.
Определить дисконт.
3.10. В течение Тлет лет на расчетный счет
в конце каждого года поступает по S руб.,
на которые т раз в году начисляются проценты по сложной годовой ставке i%. Определить сумму на расчетном счете к концу
указанного срока.
Решение:
Задание 1.
В каждом варианте приведены поквартальные данные о
кредитах от коммерческого банка на жилищное строительство (в условных единицах)
за 4 года (всего 16 кварталов, первая строка соответствует первому кварталу
первого года).
Требуется:
1)
Построить
адаптивную мультипликативную модель Хольта-Уинтерса с учетом сезонного фактора,
приняв параметры сглаживания α1=0,3; α2=0,6;
α3=0,3.
1.1.1.
Построим адаптивную мультипликативную модель
Хольта-Уинтерса с линейным ростом,
используя основную формулу:
Yp(t+k)=[a(t)+k×b(t)]×F(t+k-L)
где k – период упреждения;
Yp (t ) – расчетное значение экономического показателя для t-го периода;
F(t+k-L) – коэффициент сезонности, найденный для
соответствующего сезона в предыдущем году;
a(t), b(t), F(t) – коэффициенты сезонности, найденные для
соответствующего сезона в предыдущем году.
L – период сезонности, например для квартальных данных L=4.
Коэффициенты модели a, b, F зависит от рассматриваемого момента времени t и требует пересчета, уточнения для каждого нового момента по формулам:
a(t)=α1×Y (t )/F(t-L)+(1-α1)×[a(t-1)+b(t-1)];
b(t)=α2×[a(t)-a(t-1)]+(1+α2)×b(t-1);
F(t)=α3×Y (t )/a(t)+(1-α3)×F(t-L).
Формулы выражают адаптивный характер модели с
получением новых данных Y(t) они
позволяют получить улучшенные, уточненные коэффициенты a(t), b(t) и F(t)
Чтобы начать расчет (для t-1) предварительно нужно определить a(0), b(0) – коэффициенты
трендовой модели для предыдущего сезона.
F(-3), F(-2), F(-1), F(0) –
коэффициенты сезонности для каждого квартала предыдущего года.
Подготовим расчетную таблицу в которой включим столбцы
t1, Y(t),
a(t), b(t), F(t), Yp(t).
|
t
|
Y(t)
|
a(t)
|
b(t)
|
F(t)
|
Yp(t)
|
|
|
|
|
|
|
Рассмотрим 3 периода времени:
Предварительный
–t – от -3 до 0
Основной t – от 1 до 16
Прогнозный t – от 16 до 20
Выполним предварительный расчет.
Для
определения трендовых коэффициентов построим вспомогательную линейную регрессию
по данным за первые 8 кварталов (2 года).
|
ВЫВОД ИТОГОВ
|
|
|
|
|
Регрессионная статистика
|
|
|
|
|
|
|
|
|
Множественный R
|
0,1847873
|
|
|
|
|
|
|
|
|
R-квадрат
|
0,0341463
|
|
|
|
|
|
|
|
|
Нормированный R-квадрат
|
-0,1268293
|
|
|
|
|
|
|
|
|
Стандартная ошибка
|
10,553435
|
|
|
|
|
|
|
|
|
Наблюдения
|
8
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный анализ
|
|
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
|
|
|
Регрессия
|
1
|
23,625
|
23,625
|
0,2121212
|
0,6613303
|
|
|
|
|
Остаток
|
6
|
668,25
|
111,375
|
|
|
|
|
|
|
Итого
|
7
|
691,875
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
|
Y-пересечение
|
43,25
|
8,2231707
|
5,2595284
|
0,0019023
|
23,128612
|
63,37138846
|
23,128612
|
63,371388
|
|
Переменная X 1
|
0,75
|
1,6284304
|
0,4605662
|
0,6613303
|
-3,2346287
|
4,734628669
|
-3,2346287
|
4,7346287
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ВЫВОД ОСТАТКА
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
|
|
|
|
|
|
|
1
|
44
|
-6
|
|
|
|
|
|
|
|
2
|
44,75
|
3,25
|
|
|
|
|
|
|
|
3
|
45,5
|
11,5
|
|
|
|
|
|
|
|
4
|
46,25
|
-9,25
|
|
|
|
|
|
|
|
5
|
47
|
-7
|
|
|
|
|
|
|
|
6
|
47,75
|
4,25
|
|
|
|
|
|
|
|
7
|
48,5
|
14,5
|
|
|
|
|
|
|
|
8
|
49,25
|
-11,25
|
|
|
|
|
|
|
Используем данные, найденного значения a(0)=43,59
b(0)=0,75
Оценим коэффициент сезонности:
С помощью построенной регрессии можно рассчитать:
Y1/Y1 - коэффициент
сезонности 1 квартала 1 го года.
Y5/Y5 - коэффициент
сезонности 1 квартала 2 го года.
В
качестве оценки коэффициента сезонности 1го квартала предыдущего года, возьмем
среднее арифметическое
F(-3)=1/2[Y(1)/Yp(1)+
Y(5)/Yp(5)]=0,857
F(-2)=1/2[Y(2)/Yp(2)+
Y(6)/Yp(6)]=1,081
F(-1)=1/2[Y(3)/Yp(3)+
Y(7)/Yp(7)]=1,276
F(0) =1/2[Y(4)/Yp(4)+
Y(8)/Yp(8)]=0,786
Используем значения параметров сглаживания, заданные в
условии: α1=0,3; α2=0,6; α3=0,3.
Рассчитаем Yp(t) по основной формуле,
выбираем t=0, k=1, находим Yp(1):
Yp(1)=[a(0)+1×b(0)]×F(-3)= 37,72
Уточним коэффициент модели, полагая, что t=1, находим:
a(1)=0,3×Y(1)/F(-3)+(1-0,3)×[a(0)+b(0)]=44,10
b(1)=0,6×[a(1)-a(0)]+(1+0,6)×b(0)=0,78
F(1) =0,3× (1)/a(0)+(1-0,3)×F(0)=0,86
Аналогично определяется остальные коэффициенты и
расчетные значения Yp(t) для всех уравнений исходящих данных t-1, 2,…., 16.
|
t
|
Y(t)
|
a(t)
|
b(t)
|
F(t)
|
Yp(t)
|
|
-3
|
|
|
|
0,857
|
|
|
-2
|
|
|
|
1,081
|
|
|
-1
|
|
|
|
1,276
|
|
|
0
|
|
43,25
|
0,75
|
0,786
|
|
|
1
|
38
|
44,10
|
0,78
|
0,860
|
37,72
|
|
2
|
48
|
44,74
|
0,74
|
1,076
|
48,50
|
|
3
|
57
|
45,23
|
0,67
|
1,266
|
58,02
|
|
4
|
37
|
46,26
|
0,77
|
0,794
|
36,07
|
|
5
|
40
|
46,87
|
0,73
|
0,856
|
40,44
|
|
6
|
52
|
47,82
|
0,79
|
1,083
|
51,22
|
|
7
|
63
|
48,95
|
0,89
|
1,279
|
61,56
|
|
8
|
38
|
49,24
|
0,71
|
0,781
|
39,59
|
|
9
|
44
|
50,39
|
0,84
|
0,866
|
42,76
|
|
10
|
56
|
51,38
|
0,89
|
1,087
|
55,48
|
|
11
|
67
|
52,30
|
0,90
|
1,280
|
66,83
|
|
12
|
41
|
53,00
|
0,84
|
0,776
|
41,53
|
|
13
|
49
|
54,65
|
1,08
|
0,884
|
46,64
|
|
14
|
60
|
55,57
|
1,03
|
1,083
|
60,59
|
|
15
|
72
|
56,50
|
1,00
|
1,277
|
72,46
|
|
16
|
44
|
57,25
|
0,93
|
0,772
|
44,64
|
|
17
|
|
|
|
|
51,45
|
|
18
|
|
|
|
|
63,99
|
|
19
|
|
|
|
|
76,64
|
|
20
|
|
|
|
|
47,04
|
1.2.1.
Оценить
точность построенной модели с
использованием средней относительной ошибки аппроксимации.
Для проверки точности рассчитаем относительные
погрешности каждого уровня:
Εотн=|Ε(t)/Y(t)|×100%
По полученным результатам определим среднее значение с
помощью функции СРЗНАЧ.
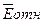=1,77(%).
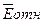=1,77 % находится в интервале (0; 5) значит точность модели
высокая.
1.3.1. Проверку случайности уровней остаточной компоненты
проводим на основании критерия поворотных точек. Для этого каждый уровень ряда Ε(t) сравниваем с
двумя соседними. Если он больше (либо меньше) обоих соседних уровней, то точка
считается поворотной.
Выделим поворотные точки и соединим их.
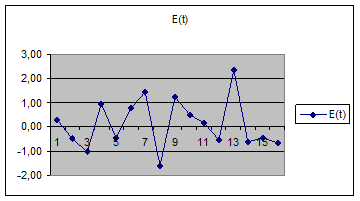
P=10
Определим по формуле p критические:
Pкр=|2(n-2)/3-1,96√(16n-29)/90|
При n=16, получим
P=10> Pкр=6=>если количество поворотных точек P больше Pкр , то
условие случайности уровней ряда остатков выполняется.
1.3.2. Для
проверки независимости остатков по d-критерию
подготовим:
d=∑|E(t)-E(t-1)|2/∑E(t)2=43,99/16,32=2,70
Полученное
значение больше 2, значит место имеет отрицательная автокорреляция. В этом
случае величину d уточняют, вычитая из 4.
d'=4-2,7=1,3.
Из таблицы выпишем критические уровни: d1=1,10; d2=1,37
d'=1,3 входит в интервал (d1; d2) =>
требуется дополнительная проверка.
Для расчета r(1) подготовим:
∑|E(t)-E(t-1)= -5,92
И вычислим r(1)= ∑[E(t)×E(t-1)]/∑E(t)2=-5,92/16,32=-0,36
Критическое
значение по таблице rкр=0,32
|r(1)|=0.36> rкр=0.32 =>
свойство независимых остатков не выполняется.
1.3.3.
Для
проверки нормального распределения остатков RS подготовим:
Emin=-1,59
Emax=2,36
Средний квадрат отклонений: S(E)= 1,04
R/S= (Emax- Emin)/S(E)= 3,82
Значение
RS для нормального распределения должно находиться в
интервале от 3,00 до 4,21.
Так
как R/S=3,82 входит в
критический интервал (3,00; 4,21), то свойство нормального распределения
остатков выполняется.
1.4.
Построим
точный прогноз на четыре квартала (т.е. на 1 год) вперед.
Для прогнозирования
используем построенную модель. Воспользуемся для этого основной формулой, в
которой t=n – фиксировано,
k-1, 2, 3, 4 – изменяется, получим:
Yp(17)=|t=16, k=1|=[a(16)+1×b(16)]×F(13)=
51,45
Yp(18)=|t=16, k=2|=[a(16)+2×b(16)]×F(14)= 63,99
Yp(19)=|t=16, k=3|=[a(16)+3×b(16)]×F(15)= 76,64
Yp(20)=|t=16, k=4|=[a(16)+4×b(16)]×F(16)= 47,04
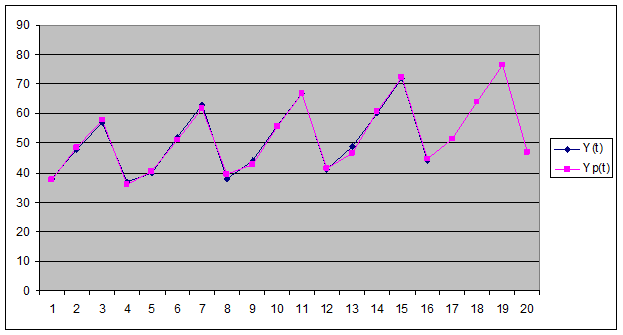
На рисунке показано сопоставление фактических и
расчетных данных. Так же показаны прогнозные данные о кредите на 1 год вперед.
Из рисунка видно, что расчетные данные хорошо согласуются с фактическими, что
говорит об удовлетворительном качестве прогноза.
Вывод: По точности модель удовлетворительная, но не является
адекватной (не выполняется свойство независимости остатков). Прогноз по этой
модели проводить не целесообразно.
Задание 2.
2.1. Рассчитаем экспоненциальную скользящую среднюю,
используя формулу:
EMAt=k×Ct+(1-k)×
EMAt-1
При
интервале сглаживания n=5, расчет
начинаем с 5 строки. Подготовим EMA5=EM5= 352,40
По формуле: EM(t)=Ct+Ct-1+Ct-2/n
где
Ct – цена закрытия t-го дня;
MAt- значение скользящего среднего текущего дня t.
Применим формулу EMAt, в
которой k=2/n+1=2/5+1=2/6
EMA6=1/3×
590+2/3× 352,40
Аналогично
рассчитываются EMA7, EMA8, EMA9, EMA10.
|
t
|
EMA(t)
|
|
1
|
|
|
2
|
|
|
3
|
|
|
4
|
|
|
5
|
352,40
|
|
6
|
431,60
|
|
7
|
487,07
|
|
8
|
518,04
|
|
9
|
543,70
|
|
10
|
555,80
|
График исходных данных C(t) и экспоненциальной
скользящей средней ЕМА(t)
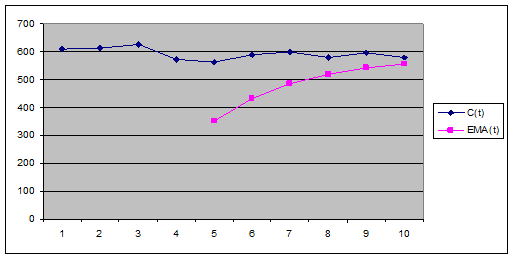
С 5 до 10 дня ЕМА ниже, чем Ct => рекомендуются покупки. Графики не пересекаются,
значит сигналов разворота нет.
2.2.
Рассчитаем
момент, по формуле:
MOMt=Ct-Ct-n
Где Ct – цена
закрытия t-го дня;
Расчет выполняется для t ≥ n+1
MOMt=C6-C6-5=590-610=-20
|
t
|
C(t)
|
MOM(t)
|
|
1
|
610
|
|
|
2
|
614
|
|
|
3
|
625
|
|
|
4
|
574
|
|
|
5
|
563
|
|
|
6
|
590
|
-20
|
|
7
|
598
|
-16
|
|
8
|
580
|
-45
|
|
9
|
595
|
21
|
|
10
|
580
|
17
|
Покажем линию момента на графике:
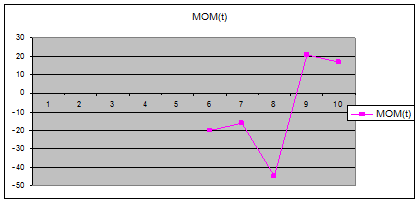
Движение графика МОМ вверх из зоны отрицательных в
зону положительных значений в точке пересечения нулевой линии дает сигнал к
покупке. С 9-го по 10-й день восходящий тренд – надо покупать.
2.3. Рассчитаем скорость изменения цен по формуле:
ROCt=Ct/Ct-n×100%
Где
Ct – цена закрытия t-го дня;
ROCt – значение ROC
текущего дня.
ROC6=С6/С6-5×100%= 590/610×100%=96,72
|
t
|
C(t)
|
ROC(t)
|
|
1
|
610
|
|
|
2
|
614
|
|
|
3
|
625
|
|
|
4
|
574
|
|
|
5
|
563
|
|
|
6
|
590
|
96,72
|
|
7
|
598
|
97,39
|
|
8
|
580
|
92,80
|
|
9
|
595
|
103,66
|
|
10
|
580
|
103,02
|
Покажем
линию скорости изменения цен на графике:
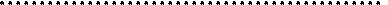
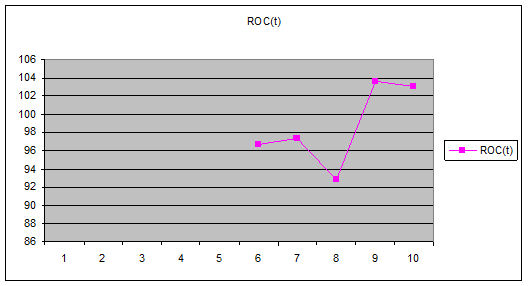
С 9-го по 10-й день
наблюдается пересечение 100% уровня, значит тренд восходящий – рекомендуются
покупки.
2.4. Рассчитаем индекс относительной силы по формуле:
RSI=100-100/(1+AU/AD)
Где AU –
сумма конечных цен за n последних
дней;
AD – сумма
убыли конечных цен за n последних
дней.
Рассчитаем изменение цен:
∆Сt=Ct-Ct-1 (начиная со второго дня)
∆Сt=C2-C1=614-610=4
|
t
|
C(t)
|
изменен.
|
|
1
|
610
|
|
|
2
|
614
|
4
|
|
3
|
625
|
11
|
|
4
|
574
|
-51
|
|
5
|
563
|
-11
|
|
6
|
590
|
27
|
|
7
|
598
|
8
|
|
8
|
580
|
-18
|
|
9
|
595
|
15
|
|
10
|
580
|
-15
|
Вычислим приросты (положительные изменения) и убытки
(отрицательные изменения):
|
t
|
C(t)
|
повышен.
|
понижен.
|
|
1
|
610
|
|
|
|
2
|
614
|
4
|
0
|
|
3
|
625
|
11
|
0
|
|
4
|
574
|
0
|
51
|
|
5
|
563
|
0
|
11
|
|
6
|
590
|
27
|
0
|
|
7
|
598
|
8
|
0
|
|
8
|
580
|
0
|
18
|
|
9
|
595
|
15
|
0
|
|
10
|
580
|
0
|
15
|
Рассчитаем
суммы приростов и убытков по n
слагаемых, начиная с n+1-го
уровня.
|
t
|
C(t)
|
AU(t,5)
|
AD(t,5)
|
|
1
|
610
|
|
|
|
2
|
614
|
|
|
|
3
|
625
|
|
|
|
4
|
574
|
|
|
|
5
|
563
|
|
|
|
6
|
590
|
42
|
62
|
|
7
|
598
|
46
|
62
|
|
8
|
580
|
35
|
80
|
|
9
|
595
|
50
|
29
|
|
10
|
580
|
50
|
33
|
По формуле рассчитаем RSI:
|
t
|
AU(t,5)
|
AD(t,5)
|
RSI(t)
|
|
1
|
|
|
|
|
2
|
|
|
|
|
3
|
|
|
|
|
4
|
|
|
|
|
5
|
|
|
|
|
6
|
42
|
62
|
40,38462
|
|
7
|
46
|
62
|
42,59259
|
|
8
|
35
|
80
|
30,43478
|
|
9
|
50
|
29
|
63,29114
|
|
10
|
50
|
33
|
60,24096
|
Покажем
линию относительной силы цен на графике:
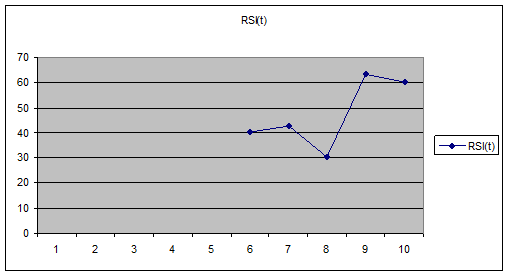
RSI
находится в центральной зоне, финансовые операции можно выполнять, нет риска в
этих операциях по сигналам других индексов.
2.5.
Рассчитаем %R, %K и %D по формулам:
%K=(Ct-Lt,n)/(Ht,n-Lt,n)×100%
%Rt=(Ht,n-Ct)/(Ht,n-Lt,n)×100%
%D=∑(Ct-Lt,n)/∑(Ht,n-Lt,n)×100%
где %K – значение закрытия текущего дня t;
%Rt – значение индекса текущего дня t
Ct – цена закрытия текущего дня t;
Lt и H5 – минимальная и максимальная цены за n предшествующих дней, до дня t.
Рассчитываем %R и %K:
|
t
|
%K
|
%R
|
|
1
|
|
|
|
2
|
|
|
|
3
|
|
|
|
4
|
|
|
|
5
|
9,09
|
90,91
|
|
6
|
43,02326
|
56,97674
|
|
7
|
52,33
|
47,67
|
|
8
|
37,5
|
62,5
|
|
9
|
73,68
|
26,32
|
|
10
|
36,17
|
63,83
|
Индекс %D рассчитывается
аналогично индексу %К, с той разницей, что при его построении величины (Ct-Lt,n) и (Ht,n-Lt,n) сглаживают, беря их трехдневную сумму.
Выберем min и max цены за 5
дней, начиная с 5-го дня.
Подготовим разности (C-L); (H-L); (H-C)
|
t
|
H(t,5)
|
L(t,5)
|
C(t)-L(t,5)
|
H(t,5)-C(t)
|
H(t,5)-L(t,5)
|
|
1
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
5
|
663
|
553
|
10
|
100
|
110
|
|
6
|
639
|
553
|
37
|
49
|
86
|
|
7
|
639
|
553
|
45
|
41
|
86
|
|
8
|
625
|
553
|
27
|
45
|
72
|
|
9
|
610
|
553
|
42
|
15
|
57
|
|
10
|
610
|
563
|
17
|
30
|
47
|
Подготовим 3-х дневные суммы для D%, начиная с 7-го уровня, заполним столбцы сумм sum(C-L) и sum(H-L). Получим:
|
t
|
sum(C-L)
|
sum(H-L)
|
%D
|
|
1
|
|
|
|
|
2
|
|
|
|
|
3
|
|
|
|
|
4
|
|
|
|
|
5
|
|
|
|
|
6
|
|
|
|
|
7
|
92,00
|
282
|
32,62
|
|
8
|
109,00
|
244
|
44,67
|
|
9
|
114,00
|
215
|
53,02
|
|
10
|
86,00
|
176
|
48,86
|
Покажем стохастические линии на графике:
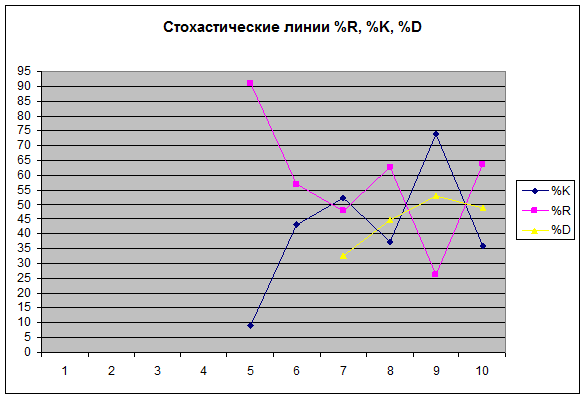
%К: 5– нижняя критическая зона перекупленности,
остановить операции.
С 6 по 10 дни – нейтральная зона.
%R: 5 день – верхняя
критическая зона перепроданности, остановить операции.
С 6 по 10 дни – нейтральная зона.
%D: С 5 по 10
дни - нейтральная зона.
Задание 3.
3.1. Банк выдал ссуду, размером 3500000 руб. Дата выдачи ссуды - 11.01.2002, возврата - 19.03.2002.
День выдачи и день возврата считать за 1 день. Проценты рассчитываются по простой
процентной ставке 40 %
годовых.
Найти:
3.1.1) точные проценты с точным числом дней ссуды;
Решение:
Денежная
сумма разовая P=3500000 руб.
Точное число дней ссуды - t=67
Операция – наращение S - ?
Простые проценты рассчитываются по формулам:
I=P×n×i
где n=t/k.
k=365;
t=67.
I=3500000×
(67/365)×0,4=256986,30 (руб.)
3.1.2)
обыкновенные проценты с точным числом дней ссуды;
I=P×n×i
где n=t/k.
k=360;
t=67.
I =3500000×
(67/360)×0,4=260555,56 (руб.)
3.1.3)
обыкновенные проценты с приближенным числом дней ссуды.
I=P×n×i
где n=t/k.
k=360;
t=67.
I =3500000× (67/360)×0,4=260555,56 (руб.)
3.2.
Через 90 дней после подписания договора должник уплатит 3500000 руб.
Кредит выдан под 40% годовых (проценты обыкновенные). Какова первоначальная
сумма и дисконт?
Решение:
Денежная сумма разовая S=3500000
Операция дисконтирование P-?
Проценты простые
i=40%, используем
математическое дисконтирование:
S=P(1+n∙i)=>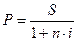
, где n=t/k.
АСТ/360:
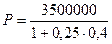= 3181818,18
руб.
D=S-P=3500000-3181818=318181,8 (руб)
3.3. Через 90
дней предприятие должно получить по векселю 3500000 руб. Банк приобрел этот вексель с дисконтом. Банк учел
вексель по учетной ставке 40% годовых (год равен 360 дням). Определить
полученную предприятием сумму и дисконт.
Решение:
S=3500000 руб.
t=90 дней
процент
простой i=40%
Используем
формулы:
D=Snd=3500000×90/360×0,4= 350000
P=S-D=3500000-350000= 3150000
3.4. В кредитном договоре на сумму 3500000руб. и сроком
на 5 лет, зафиксирована ставка
сложных процентов, равная 40% годовых. Определить наращенную сумму.
Решение:
Денежная
сумма разовая Р=3500000
Операция
наращение сложных процентов S-?
Используем
функцию БС:
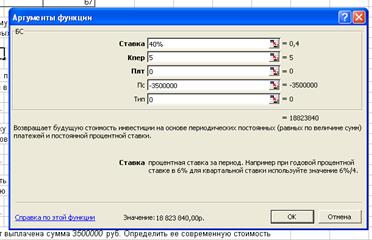
БС= 18 823 840 руб.
3.5. Ссуда размером 3500000руб. предоставлена на 5 лет.
Проценты сложные, ставка - 40% годовых. Проценты начисляются 4 раза в год.
Вычислить наращенную сумму.
Решение:
Денежная
сумма разовая P=3500000
Операция наращение S-?
Проценты сложные i=40%
Число
периодов m=4
Число
кварталов (5×4)=20
Используем
функцию БС:
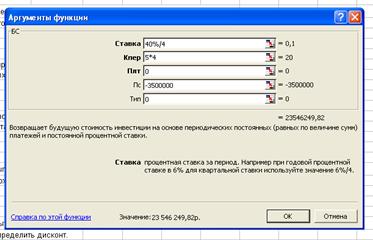
БС= 23 546 249,82р.
3.6. Вычислить эффективную ставку процента, если банк
начисляет проценты 4 раза в год, исходя из номинальной ставки 40% годовых.
Решение:
Используем
функцию ЭФФЕКТ:
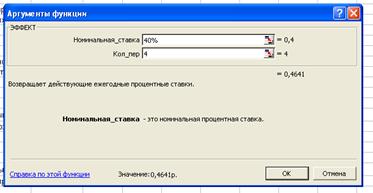
iэ= 0,4641р.
3.7. Определить, какой должна быть номинальная ставка при
начислении процентов 4 раза в год, чтобы обеспечить аффективную ставку 40%
годовых.
Решение:
Используем
функцию НОМИНАЛ:
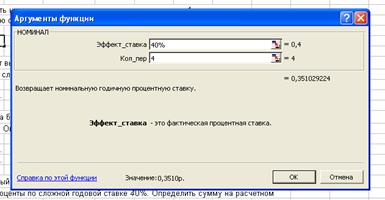
Iн= 0,3510р.
3.8. Через 5 лет предприятию будет выплачена сумма 3500000руб.
Определить ее современную стоимость при условии, что применяется сложная процентная
ставка 40% годовых.
Решение:
Денежная
сумма разовая S=3 500 000
Операция дисконтирование P-?
Проценты сложные i=40%
Для
расчета используем функцию ПС:
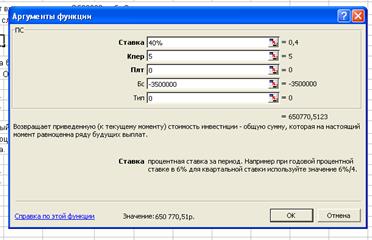
ПС= 650 770,51руб.
3.9. Через 5 лет по векселю должна быть выплачена сумма 3500000руб.
Банк учел вексель по сложной учетной ставке 40% годовых. Определить дисконт.
Решение:
Денежная
сумма разовая S=3 500 000
Операция дисконтирование P-?
Проценты сложные d=40%
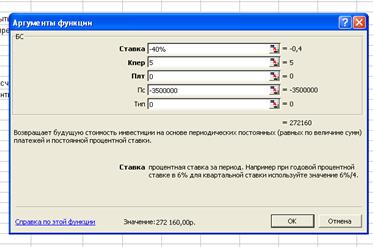
БС= 272 160,00руб.
D=S-P
D =3500000-272 160=3 227
840,00руб.
3.10.
В течение 5 лет на расчетный счет в
конце каждого года поступает по 3500000руб., на которые 4 раза в год
начисляются проценты по сложной годовой ставке 40%. Определить сумму на
расчетном счете к концу указанного срока.
Денежная
сумма разовая P=3500000 (год)
Операция наращение S-?
Проценты сложные i=40% (квартал)
m=4≠p=1,
перейдем к эффективной процентной ставке:
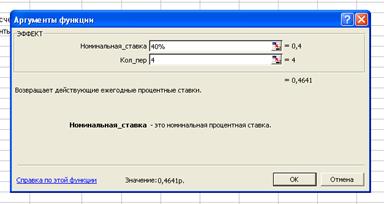
Определения
суммы на расчетном счете к концу указанного срока:
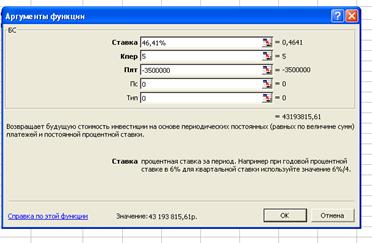
БС= 43 193 815,61руб.